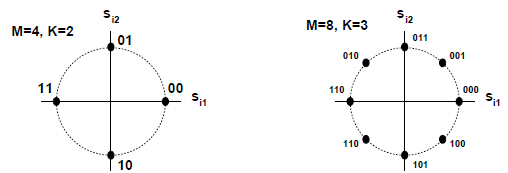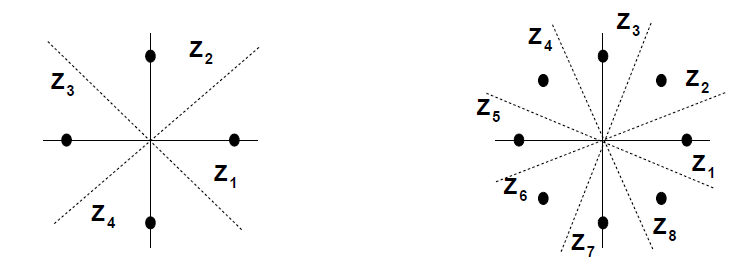Wireless Communications (Andrea Goldsmith)学习笔记。
本书第五、六章主要介绍数字调制及其性能和同步原理的部分内容。
数字调制的优势:传输速率高,纠错能力强,抗信道失真,高效的多址接入和更好的安全和隐私性。
选择数字调制的考虑因素:
高传输速率
高频带利用率(最小化带宽占用)
高功率利用率(最小化发射功率)
对信道失真的稳健性(最小化误比特率/误信率)
低功耗,低成本
数字调制的分类:
linear modulation(线性调制):调幅,调相
有更好的频谱特性
易受到衰落和干扰的影响
需要昂贵功率利用率差的线性放大器
constant envelope modulation (nonlinear modulation,恒包络调制,非线性调制):调频
trade-off of linear or nonlinear modulation
线性调制:频带利用率更佳
非线性调制:功率利用率更佳,抗信道失真的干扰更强
其它数字调制需要考虑的方面:
星座大小(constellations):星座越大,给定带宽传输速率越高,对噪声、衰落和硬件干扰性能变差。
是否需要相干载波(coherent reference):实现困难
数字调制的主要性能指标:
错误率(可靠性指标):误码率和误比特率(误信率)
中断率:瞬时SNR低于门限的概率
无线信道传输过程中各种损耗带来的影响:
频率选择性衰落带来ISI,ISI又会造成error floor
多普勒频移会带来频谱扩展,频谱扩展会造成adjacent channel interference(邻信道干扰)。还会给差分编码造成不可避免的error floor
数字调制与解调直观来说就是接收机将接收信号和所有可能出现的发射信号比较,选择最接近的作为检测结果,从而使得错误率最低。信号空间就是将信号embed到一个向量空间中,从而可以比较他们的接近程度。
符号说明:
系统以T T T K = log 2 M K=\log_2M K = log 2 M
在时间间隔[ k T , ( k + 1 ) T ) [kT,(k+1)T) [ k T , ( k + 1 ) T ) K K K m i = { b 1 , ⋯ , b K } m_i=\{b_1,\cdots,b_K\} m i = { b 1 , ⋯ , b K }
数字域所有可能发射消息所构成的集合M \mathcal{M} M m i ∈ M ( i = 1 , 2 , ⋯ , M = 2 K ) m_i\in\mathcal{M}(i=1,2,\cdots, M=2^K) m i ∈ M ( i = 1 , 2 , ⋯ , M = 2 K )
模拟域所有发射消息所构成的集合S \mathcal{S} S s i ( t ) ∈ S ( i = 1 , 2 , ⋯ , M = 2 K ) s_i(t)\in\mathcal{S}(i=1,2,\cdots, M=2^K) s i ( t ) ∈ S ( i = 1 , 2 , ⋯ , M = 2 K )
一段时间内发射的消息是模拟域发射消息的组合
s ( t ) = ∑ k s i ( t − k T ) s(t)=\sum_ks_i(t-kT)
s ( t ) = k ∑ s i ( t − k T )
接收信号为r ( t ) = s ( t ) + n ( t ) r(t)=s(t)+n(t) r ( t ) = s ( t ) + n ( t ) [ k T , ( k + 1 ) T ) [kT,(k+1)T) [ k T , ( k + 1 ) T ) r ( t ) r(t) r ( t ) s i ( t ) , m i s_i(t),m_i s i ( t ) , m i m ^ \hat m m ^
接收机的目标——错误率最小
P e = ∑ i = 1 M p ( m ^ ≠ m i ∣ 发射序列为 m i ) p ( 发射序列为 m i ) = N e r r o r N P_e=\sum_{i=1}^Mp(\hat m \ne m_i|\text{发射序列为}m_i)p(\text{发射序列为}m_i)=\frac{N_{error}}{N}
P e = i = 1 ∑ M p ( m ^ = m i ∣ 发射序列为 m i ) p ( 发射序列为 m i ) = N N e r r o r
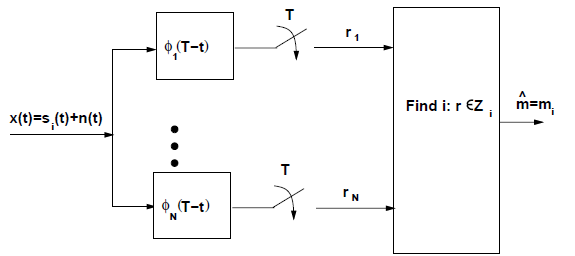
将M M M S = { s 1 ( t ) , s 2 ( t ) , ⋯ , s M ( t ) } \mathcal{S}=\{s_1(t), s_2(t),\cdots, s_M(t) \} S = { s 1 ( t ) , s 2 ( t ) , ⋯ , s M ( t ) } N ( ≤ M ) N(\le M) N ( ≤ M ) { ϕ 1 ( t ) , ϕ 2 ( t ) , ⋯ , ϕ N ( t ) } \{\phi_1(t), \phi_2(t),\cdots,\phi_N(t) \} { ϕ 1 ( t ) , ϕ 2 ( t ) , ⋯ , ϕ N ( t ) }
s i ( t ) = ∑ j = 1 M s i j ϕ j ( t ) s_i(t)=\sum_{j=1}^Ms_{ij}\phi_{j}(t)
s i ( t ) = j = 1 ∑ M s i j ϕ j ( t )
the minimum number N N N s i ( t ) s_i(t) s i ( t ) T T T B B B 2 B T 2BT 2 B T
For linear passband modulation techniques, the basis set consists of the sine and cosine function with 2 T \sqrt{\frac{2}{T}} T 2
The simplest pulse shape that satisfies the orthonormal properties is the rectangular pulse shape g ( t ) = 2 T ( 0 ≤ t < T ) g(t) =\sqrt{\frac{2}{T}}(0\le t<T) g ( t ) = T 2 ( 0 ≤ t < T )
信号的星座点与星座图
信号的星座点(signal constellation point) :将s i ( t ) s_i(t) s i ( t ) { s i j } \{s_{ij}\} { s i j } s i = ( s i 1 , s i 2 , ⋯ . s i N ) ∈ R N \mathbf{s}_i=(s_{i1},s_{i2},\cdots.s_{iN})\in\mathbb{R}^N s i = ( s i 1 , s i 2 , ⋯ . s i N ) ∈ R N 星座图(signal constellation) :所有星座点构成的集合{ s 1 , s 2 , ⋯ , s M } \{\mathbf{s}_1,\mathbf{s}_2 ,\cdots,\mathbf{s}_M\} { s 1 , s 2 , ⋯ , s M } 信号s i ( t ) s_i(t) s i ( t ) s i \mathbf{s}_i s i 信号空间表示(signal space representation)
包含所有星座点的向量空间称为信号空间(signal space)
向量的长度与距离
向量的长度(length):
∣ ∣ s i ∣ ∣ = ∑ j = 1 N s i j 2 ||\mathbf{s}_i||=\sqrt{\sum_{j=1}^Ns_{ij}^2}
∣ ∣ s i ∣ ∣ = j = 1 ∑ N s i j 2
向量之间的距离(distance):
∣ ∣ s i − s k ∣ ∣ = ∑ j = 1 N ( s i j − s k j ) 2 = ∫ 0 T ( s i ( t ) − s k ( t ) ) 2 d t ||\mathbf{s}_i-\mathbf{s}_k ||=\sqrt{\sum_{j=1}^N(s_{ij}-s_{kj})^2}=\sqrt{\int_0^T(s_{i}(t)-s_{k}(t))^2\mathrm{d}t}
∣ ∣ s i − s k ∣ ∣ = j = 1 ∑ N ( s i j − s k j ) 2 = ∫ 0 T ( s i ( t ) − s k ( t ) ) 2 d t
第二个等号通过正交基底的正交性获得
使用正交基底,将接收信号r ( t ) r(t) r ( t )
使用最大似然接收机
接收信号:
r ( t ) = ∑ j = 1 N ( s i j + n j ) ϕ j ( t ) + n r ( t ) = ∑ j = 1 N r j ϕ j ( t ) + n r ( t ) r(t)=\sum_{j=1}^N(s_{ij}+n_j)\phi_j(t)+n_r(t)=\sum_{j=1}^Nr_j\phi_j(t)+n_r(t)
r ( t ) = j = 1 ∑ N ( s i j + n j ) ϕ j ( t ) + n r ( t ) = j = 1 ∑ N r j ϕ j ( t ) + n r ( t )
n r ( t ) n_r(t) n r ( t )
充分统计量(sufficient statistic):对s i \mathbf{s}_i s i r ( t ) r(t) r ( t ) n r ( t ) n_r(t) n r ( t ) m ^ \hat m m ^ r = ( r 1 , r 2 , ⋯ , r N ) \mathbf{r}=(r_1,r_2,\cdots,r_N) r = ( r 1 , r 2 , ⋯ , r N ) r \mathbf{r} r r ( t ) r(t) r ( t )
直观上可以看到n r ( t ) n_r(t) n r ( t )
数学上可以证明发射信号与噪声是相互独立的,故s i j s_{ij} s i j n r ( t ) n_r(t) n r ( t )
max p ( m ^ = m i ∣ r ( t ) ) ⇔ max p ( 发射星座点为 s i ∣ r ( t ) ) \max p(\hat m=m_i|r(t))\Leftrightarrow\max p(\text{发射星座点为}\mathbf{s}_i|r(t))
max p ( m ^ = m i ∣ r ( t ) ) ⇔ max p ( 发射星座点为 s i ∣ r ( t ) )
可以证明上式等于p ( 发射信号为 ( s i 1 , s i 2 , ⋯ , s i N ) ∣ ( r 1 , r 2 , ⋯ , r N ) ) p(\text{发射信号为}(s_{i1},s_{i2},\cdots,s_{iN})|(r_1,r_2,\cdots,r_N)) p ( 发射信号为 ( s i 1 , s i 2 , ⋯ , s i N ) ∣ ( r 1 , r 2 , ⋯ , r N ) ) n r ( t ) n_r(t) n r ( t ) r \mathbf{r} r
由于r \mathbf{r} r r ( t ) r(t) r ( t ) r \mathbf{r} r r ( t ) r(t) r ( t )
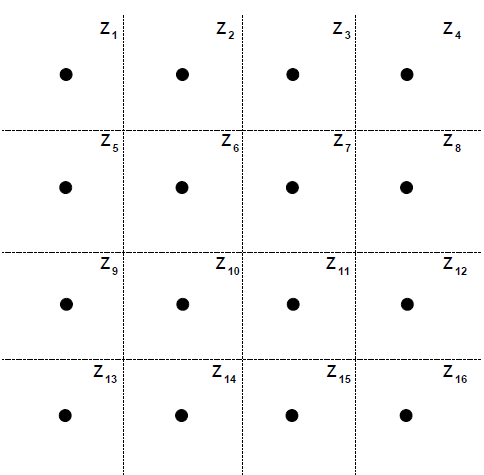
判决域(decisions regions)——信号空间的子集
Z i = { r : p ( 发射星座点为 s i ∣ r ) > p ( 发射星座点为 s j ∣ r ) ∀ j ≠ i } Z_i=\{\mathbf{r}:p(\text{发射星座点为}\mathbf{s}_i|\mathbf{r})>p(\text{发射星座点为}\mathbf{s}_j|\mathbf{r})\forall j\ne i\}
Z i = { r : p ( 发射星座点为 s i ∣ r ) > p ( 发射星座点为 s j ∣ r ) ∀ j = i }
即在已知接收向量时,发射星座点为s i \mathbf{s}_i s i s i \mathbf{s}_i s i
最大似然接收机
arg max s i p ( r ∣ s i ) ( i = 1 , ⋯ , M ) \arg\max_{\mathbf{s}_i}p(\mathbf{r}|\mathbf{s}_i)(i=1,\cdots, M)
arg s i max p ( r ∣ s i ) ( i = 1 , ⋯ , M )
最大化似然函数L ( s i ) = p ( r ∣ s i ) L(\mathbf{s}_i)=p(\mathbf{r}|\mathbf{s}_i) L ( s i ) = p ( r ∣ s i ) r \mathbf{r} r s i \mathbf{s}_i s i
Z i = ( r : ∥ r − s i ∥ < ∥ r − s j ∥ ∀ j = 1 , … , M , j ≠ i ) i = 1 , … , M Z_{i}=\left(\mathbf{r}:\left\|\mathbf{r}-\mathbf{s}_{i}\right\|<\left\|\mathbf{r}-\mathbf{s}_{j}\right\| \forall j=1, \ldots, M, j \neq i\right) \quad i=1, \ldots, M
Z i = ( r : ∥ r − s i ∥ < ∥ r − s j ∥ ∀ j = 1 , … , M , j = i ) i = 1 , … , M
匹配滤波器是另一种接收机结构,两种接收机是等价的。
数字带通调制就是利用载波携带消息信号在信道中传输。调制的目的就是以更高速率传输的同时最下滑数据损失的概率。
已调信号的表示形式:
s ( t ) = α ( t ) cos [ 2 π ( f c + f ( t ) ) t + θ ( t ) + ϕ 0 ] = α ( t ) cos ( 2 π f c t + ϕ ( t ) + ϕ 0 ) s(t)=\alpha(t) \cos \left[2 \pi\left(f_{c}+f(t)\right) t+\theta(t)+\phi_{0}\right]=\alpha(t) \cos \left(2 \pi f_{c} t+\phi(t)+\phi_{0}\right)
s ( t ) = α ( t ) cos [ 2 π ( f c + f ( t ) ) t + θ ( t ) + ϕ 0 ] = α ( t ) cos ( 2 π f c t + ϕ ( t ) + ϕ 0 )
其中,α ( t ) \alpha(t) α ( t ) f ( t ) f(t) f ( t ) θ ( t ) \theta(t) θ ( t ) ϕ ( t ) = 2 π f ( t ) + θ ( t ) \phi(t)=2\pi f(t)+\theta(t) ϕ ( t ) = 2 π f ( t ) + θ ( t ) ϕ 0 \phi_0 ϕ 0
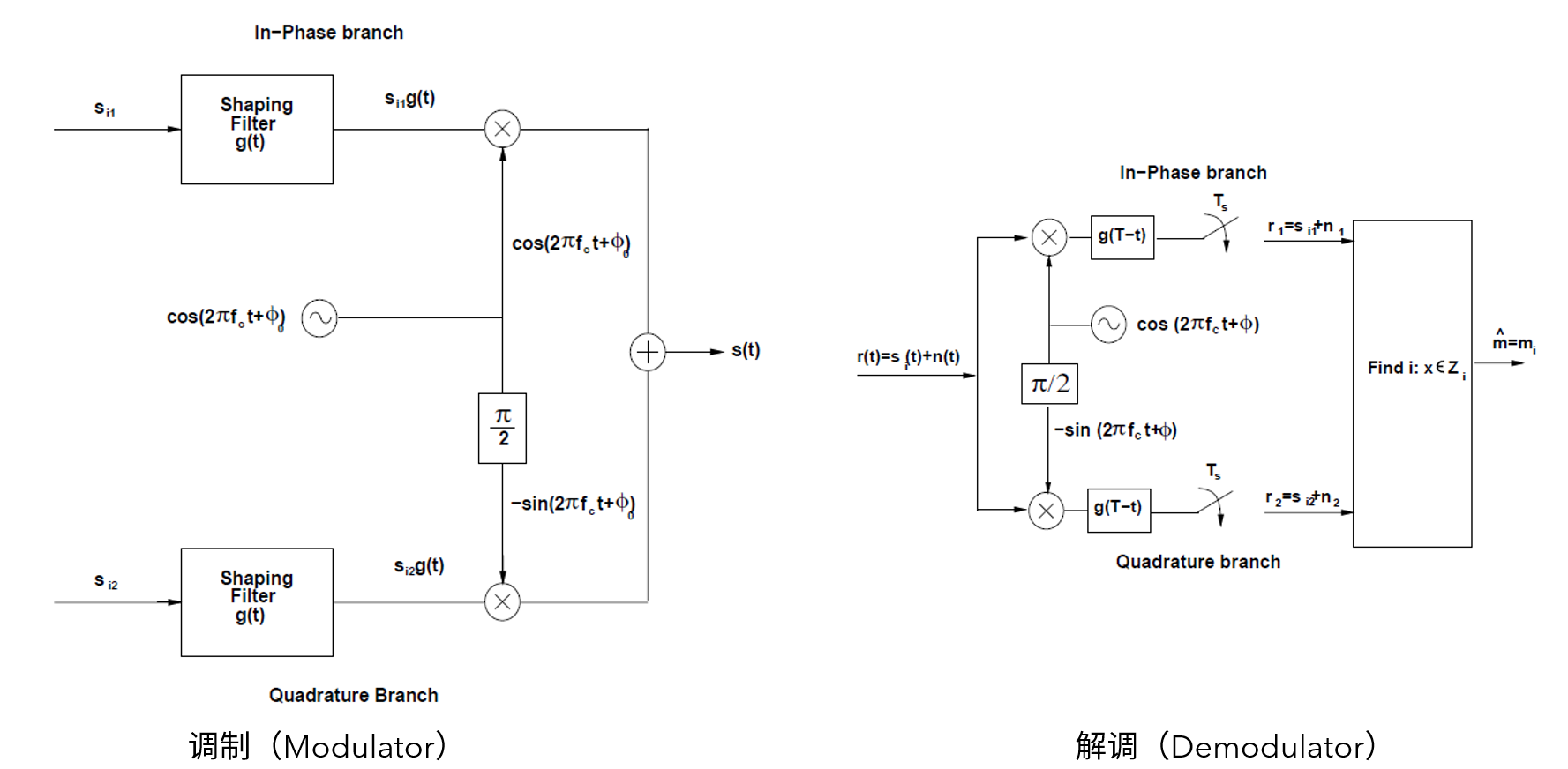
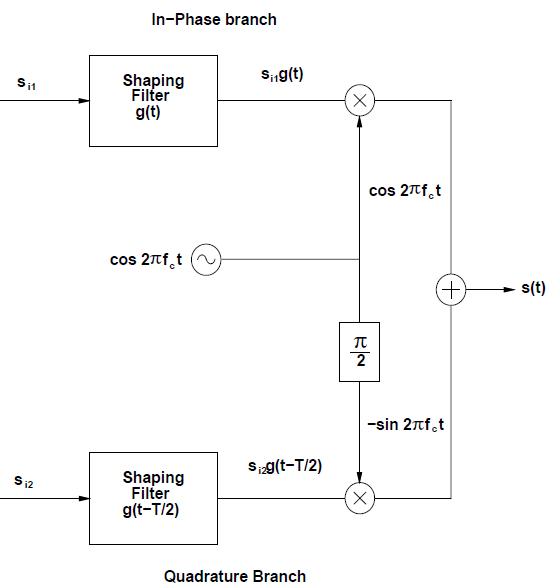
已调信号的正交表示和复包络表示
s ( t ) = α ( t ) cos ϕ ( t ) cos ( 2 π f c t ) − α ( t ) sin ϕ ( t ) sin ( 2 π f c t ) = s I ( t ) cos ( 2 π f c t ) − s Q ( t ) sin ( 2 π f c t ) = ℜ { u ( t ) e j 2 π f c t } \begin{aligned}
s(t)=&\alpha(t) \cos \phi(t) \cos \left(2 \pi f_{c} t\right)-\alpha(t) \sin \phi(t) \sin \left(2 \pi f_{c} t\right)\\=&s_{I}(t) \cos \left(2 \pi f_{c} t\right)-s_{Q}(t) \sin \left(2 \pi f_{c} t\right)\\
=&\Re\{u(t)e^{j2\pi f_ct} \}
\end{aligned}
s ( t ) = = = α ( t ) cos ϕ ( t ) cos ( 2 π f c t ) − α ( t ) sin ϕ ( t ) sin ( 2 π f c t ) s I ( t ) cos ( 2 π f c t ) − s Q ( t ) sin ( 2 π f c t ) ℜ { u ( t ) e j 2 π f c t }
其中,u ( t ) = s I ( t ) + j s Q ( t ) u(t)=s_I(t)+js_Q(t) u ( t ) = s I ( t ) + j s Q ( t )
AM/PM信号的信号空间表示
s ( t ) = s i 1 ϕ 1 ( t ) + s i 2 ϕ 2 ( t ) s(t)=s_{i1}\phi_1(t)+s_{i2}\phi_2(t)
s ( t ) = s i 1 ϕ 1 ( t ) + s i 2 ϕ 2 ( t )
其中,ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t + ϕ 0 ) \phi_1(t)=g(t)\cos(2\pi f_c t+\phi_0) ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t + ϕ 0 ) ϕ 1 ( t ) = − g ( t ) sin ( 2 π f c t + ϕ 0 ) \phi_1(t)=-g(t)\sin(2\pi f_c t+\phi_0) ϕ 1 ( t ) = − g ( t ) sin ( 2 π f c t + ϕ 0 )
AM/PM信号的复包络表示
s ( t ) = ℜ { x ( t ) e j ϕ 0 e j 2 π f c t } s(t)=\Re\{x(t)e^{j\phi_0}e^{j2\pi f_c t} \}
s ( t ) = ℜ { x ( t ) e j ϕ 0 e j 2 π f c t }
其中,x ( t ) = ( s i 1 + j s i 2 ) g ( t ) x(t)=(s_{i1}+js_{i2})g(t) x ( t ) = ( s i 1 + j s i 2 ) g ( t ) s i = { s i 1 , s i 2 } \mathbf{s}_i=\{s_{i1},s_{i2}\} s i = { s i 1 , s i 2 } log 2 M \log_2 M log 2 M T s T_s T s
R = log 2 M T s ( b p s ) R=\frac{\log_2M}{T_s}(bps)
R = T s log 2 M ( b p s )
AM/PM的分类
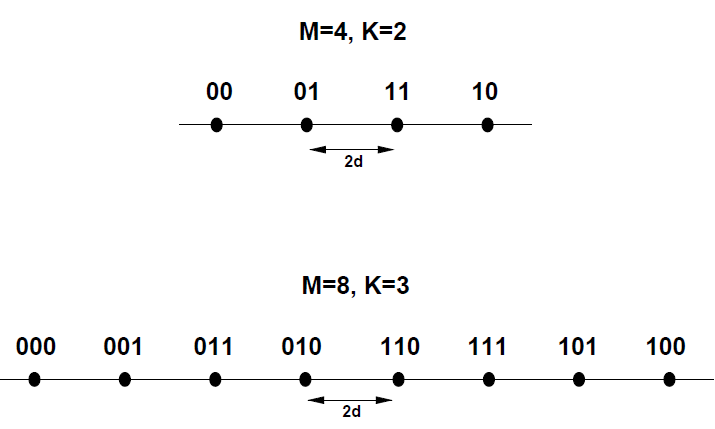
M进制 脉幅调制(Pulse Amplitude Modulation, MPAM): information encoded in amplitude only.M进制 相移键控(Phase Shift Keying, MPSK): information encoded in phase only.正交振幅调制(Quadrature Amplitude Modulation, MQAM): information encoded in both amplitude and phase.
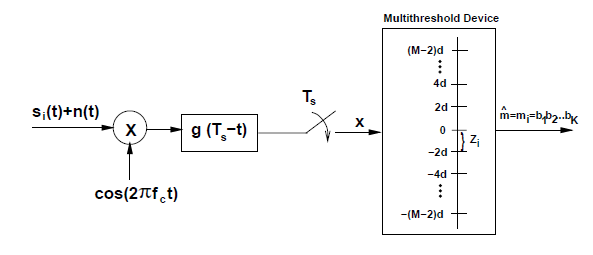
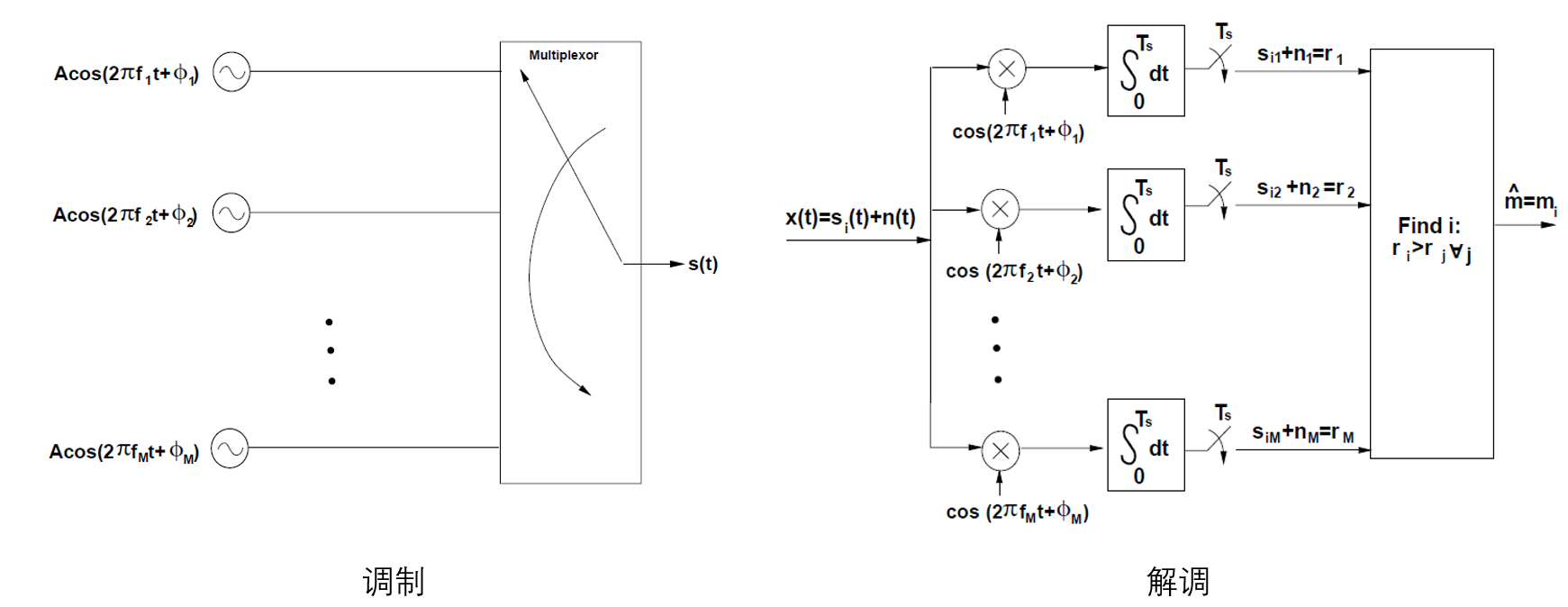
AM/PM调制与解调
载波相位恢复(carrier phase recovery)→相干解调(coherent detection)
码元同步(synchronization)
发射信号
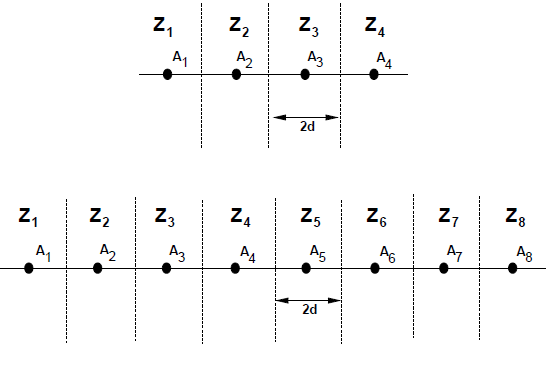
判决域
Z i = { ( − ∞ , A i + d ) i = 1 [ A i − d , A i + d ) 2 ≤ i ≤ M − 1 [ A i − d , ∞ ) i = M Z_{i}=\left\{\begin{array}{ll}\left(-\infty, A_{i}+d\right) & i=1 \\ {\left[A_{i}-d, A_{i}+d\right)} & 2 \leq i \leq M-1 \\ {\left[A_{i}-d, \infty\right)} & i=M\end{array}\right.
Z i = ⎩ ⎨ ⎧ ( − ∞ , A i + d ) [ A i − d , A i + d ) [ A i − d , ∞ ) i = 1 2 ≤ i ≤ M − 1 i = M
MPAM只有一个基函数ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t + ϕ 0 ) \phi_1(t)=g(t)\cos(2\pi f_ct+\phi_0) ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t + ϕ 0 )
MPAM的相干解调器
发射信号(圆上等间隔分布)
s i ( t ) = ℜ { A g ( t ) e j 2 π ( i − 1 ) / M e j 2 π f c t } , 0 ≤ t ≤ T s = A g ( t ) cos [ 2 π f c t + 2 π ( i − 1 ) M ] = A g ( t ) cos [ 2 π ( i − 1 ) M ] cos 2 π f c t − A g ( t ) sin [ 2 π ( i − 1 ) M ] sin 2 π f c t . \begin{aligned}
s_{i}(t) &=\Re\left\{A g(t) e^{j 2 \pi(i-1) / M} e^{j 2 \pi f_{c} t}\right\}, \quad 0 \leq t \leq T_{s} \\
&=A g(t) \cos \left[2 \pi f_{c} t+\frac{2 \pi(i-1)}{M}\right] \\
&=A g(t) \cos \left[\frac{2 \pi(i-1)}{M}\right] \cos 2 \pi f_{c} t-A g(t) \sin \left[\frac{2 \pi(i-1)}{M}\right] \sin 2 \pi f_{c} t .
\end{aligned}
s i ( t ) = ℜ { A g ( t ) e j 2 π ( i − 1 ) / M e j 2 π f c t } , 0 ≤ t ≤ T s = A g ( t ) cos [ 2 π f c t + M 2 π ( i − 1 ) ] = A g ( t ) cos [ M 2 π ( i − 1 ) ] cos 2 π f c t − A g ( t ) sin [ M 2 π ( i − 1 ) ] sin 2 π f c t .
星座点由s i 1 = A cos [ 2 π ( i − 1 ) M ] s_{i 1}=A \cos \left[\frac{2 \pi(i-1)}{M}\right] s i 1 = A cos [ M 2 π ( i − 1 ) ] s i 2 = A sin [ 2 π ( i − 1 ) M ] s_{i 2}=A \sin \left[\frac{2 \pi(i-1)}{M}\right] s i 2 = A sin [ M 2 π ( i − 1 ) ]
相移θ i = 2 π ( i − 1 ) M \theta_i=\frac{2\pi(i-1)}{M} θ i = M 2 π ( i − 1 )
星座图最小距离d min = 2 A sin ( π M ) d_{\min}=2A\sin\left(\frac{\pi}{M}\right) d min = 2 A sin ( M π )
第i i i
判决域
Z i = { r e j θ : 2 π ( i − 0.5 ) M ≤ θ < 2 π ( i + 0.5 ) M } Z_i=\left\{re^{j\theta}:\frac{2\pi(i-0.5)}{M}\le\theta<\frac{2\pi(i+0.5)}{M} \right\}
Z i = { r e j θ : M 2 π ( i − 0 . 5 ) ≤ θ < M 2 π ( i + 0 . 5 ) }
MPSK含有同相分量和正交分量
2PSK的相干解调
2PSK只有一个基函数ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t ) \phi_{1}(t)=g(t) \cos \left(2 \pi f_{c} t\right) ϕ 1 ( t ) = g ( t ) cos ( 2 π f c t )
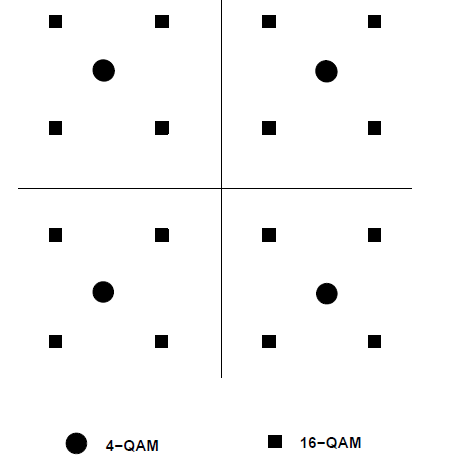
MQAM有两个自由度,幅度和相位均携带信息,故有更高的频谱利用率。
发射信号(下述对正方形星座分析)
s i ( t ) = ℜ { A i e j θ i g ( t ) e j 2 π f c t } = A i cos ( θ i ) g ( t ) cos ( 2 π f c t ) − A i sin ( θ i ) g ( t ) sin ( 2 π f c t ) , 0 ≤ t ≤ T s s_{i}(t)=\Re\left\{A_{i} e^{j \theta_{i}} g(t) e^{j 2 \pi f_{c} t}\right\}=A_{i} \cos \left(\theta_{i}\right) g(t) \cos \left(2 \pi f_{c} t\right)-A_{i} \sin \left(\theta_{i}\right) g(t) \sin \left(2 \pi f_{c} t\right), \quad 0 \leq t \leq T_{s}
s i ( t ) = ℜ { A i e j θ i g ( t ) e j 2 π f c t } = A i cos ( θ i ) g ( t ) cos ( 2 π f c t ) − A i sin ( θ i ) g ( t ) sin ( 2 π f c t ) , 0 ≤ t ≤ T s
任意两个星座点的距离d i j = ∥ s i − s j ∥ = ( s i 1 − s j 1 ) 2 + ( s i 2 − s j 2 ) 2 d_{i j}=\left\|\mathbf{s}_{i}-\mathbf{s}_{j}\right\|=\sqrt{\left(s_{i 1}-s_{j 1}\right)^{2}+\left(s_{i 2}-s_{j 2}\right)^{2}} d i j = ∥ s i − s j ∥ = ( s i 1 − s j 1 ) 2 + ( s i 2 − s j 2 ) 2 d min = 2 d d_{\min}=2d d min = 2 d
星座点由s i 1 , s i 2 s_{i 1},s_{i2} s i 1 , s i 2 ( 2 i − 1 − L ) d , i = 1 , 2 , ⋯ , L = 2 l (2i-1-L)d,i=1,2,\cdots,L=2^l ( 2 i − 1 − L ) d , i = 1 , 2 , ⋯ , L = 2 l
星座图——正方形星座
有M = L 2 = 2 2 l M=L^2=2^{2l} M = L 2 = 2 2 l
2 l 2l 2 l 每维度多传1 bit,即每symbol多传2 bits,需要增加6 dB能量来保持星座图最小距离不变
判决域
差分调制(Differential Modulation)
差分调制属于更普遍的带记忆的调制类别,在时间[ k T s , ( k + 1 ) T s ) [kT_s, (k + 1)T_s) [ k T s , ( k + 1 ) T s )
差分调制的基本原理是将先前的符号作为当前符号的相位参考,从而避免了在接收端需要相干相位参考。
差分相干解调
差分编码对随机相位漂移不敏感,单对系统性的多普勒频移敏感,多普勒频移会造成error floor。
星座成形(Constellation Shaping)
if a complex channel code is already being used and little further improvement can be obtained by a more complex code, constellation shaping may obtain around 1 dB of additional gain.
正交偏移(Quadrature Offset)
为防止信号倒相引起180度相移,将正交分量g ( t ) g(t) g ( t )
Phase modulation with phase offset is usually abbreviated as O-MPSK, 例如π 4 \frac{\pi}{4} 4 π
FM信号的空间表示
s i ( t ) = ∑ j s i j ϕ j ( t ) = A ϕ i ( t ) s_i(t)=\sum_js_{ij}\phi_j(t)=A\phi_i(t)
s i ( t ) = j ∑ s i j ϕ j ( t ) = A ϕ i ( t )
其中,s i j = A δ ( i − j ) s_{ij}=A\delta(i-j) s i j = A δ ( i − j ) ϕ j ( t ) = cos ( 2 π f j t + ϕ j ) \phi_j(t)=\cos(2\pi f_jt +\phi_j) ϕ j ( t ) = cos ( 2 π f j t + ϕ j ) ϕ i = ϕ j \phi_i=\phi_j ϕ i = ϕ j 1 2 T s \frac{1}{2T_s} 2 T s 1
调频信号的特点
FM信号的调制与解调
解调器要求第j j j j j j
载波相位不一致ϕ i ≠ ϕ j \phi_i\ne \phi_j ϕ i = ϕ j
FSK(Frequency Shift Keying)发射信号
s i ( t ) = A cos [ 2 π f c t + 2 π α i Δ f c t + ϕ i ] , 0 ≤ t < T s s_{i}(t)=A \cos \left[2 \pi f_{c} t+2 \pi \alpha_{i} \Delta f_{c} t+\phi_{i}\right], \quad 0 \leq t<T_{s}
s i ( t ) = A cos [ 2 π f c t + 2 π α i Δ f c t + ϕ i ] , 0 ≤ t < T s
频移项系数α i = ( 2 i − 1 − M ) . i = 1 , 2 , ⋯ , M = 2 K \alpha_i=({2i-1-M}).i=1,2,\cdots,M=2^K α i = ( 2 i − 1 − M ) . i = 1 , 2 , ⋯ , M = 2 K
基函数ϕ i ( t ) = 2 T s cos [ 2 π f c t + 2 π α i Δ f c t + ϕ i ] \phi_{i}(t)=\sqrt{\frac 2{T_{s}}} \cos \left[2 \pi f_{c} t+2 \pi \alpha_{i} \Delta f_{c} t+\phi_{i}\right] ϕ i ( t ) = T s 2 cos [ 2 π f c t + 2 π α i Δ f c t + ϕ i ]
最小频率间隔2 Δ f c 2\Delta f_c 2 Δ f c
2FSK:只有两种频率变化
MSK(Minimum Shift Keying):对于2FSK,当ϕ 1 = ϕ 2 \phi_1=\phi_2 ϕ 1 = ϕ 2 2 Δ f = 1 2 T s 2\Delta f=\frac{1}{2T_s} 2 Δ f = 2 T s 1
用数字基带信号调制单音载波,构成Continuous-Phase FSK(CPFSK)信号
s i ( t ) = A cos [ 2 π f c t + 2 π β ∫ − ∞ t u ( τ ) d τ ] = A cos [ 2 π f c t + θ ( t ) ] s_{i}(t)=A \cos \left[2 \pi f_{c} t+2 \pi \beta \int_{-\infty}^{t} u(\tau) d \tau\right]=A \cos \left[2 \pi f_{c} t+\theta(t)\right]
s i ( t ) = A cos [ 2 π f c t + 2 π β ∫ − ∞ t u ( τ ) d τ ] = A cos [ 2 π f c t + θ ( t ) ]
卡森带宽(Carson):B s ≈ M Δ f c + B g B_s\approx M\Delta f_c+B_g B s ≈ M Δ f c + B g B g B_g B g
The spectral efficiency penalty of CPFSK increases with data rate.
Coherent detection of CPFSK can be done symbol-by-symbol or over a sequence of symbols.
当第i i i m i m_i m i
Nyquist准则:
时域:p ( k T s ) = { p 0 = p ( 0 ) k = 0 0 k ≠ 0 p\left(k T_{s}\right)=\left\{\begin{array}{ll}
p_{0}=p(0) & k=0 \\
0 & k \neq 0
\end{array}\right. p ( k T s ) = { p 0 = p ( 0 ) 0 k = 0 k = 0
频域:∑ l = − ∞ ∞ P ( f + l T s ) = p 0 T s \sum_{l=-\infty}^{\infty}P(f+\frac{l}{T_s})=p_0T_s ∑ l = − ∞ ∞ P ( f + T s l ) = p 0 T s
几种脉冲:
Rectangular pulses(矩形脉冲)
g ( t ) = 2 T s g(t)=\sqrt{\frac 2{T_s}}
g ( t ) = T s 2
等效三角脉冲:
p ( t ) = { 2 + 2 t / T s − T s ≤ t < 0 2 − 2 t / T s 0 ≤ t < T s 0 else p(t)=\left\{\begin{array}{ll}2+2 t / T_{s} & -T_{s} \leq t<0 \\ 2-2 t / T_{s} & 0 \leq t<T_{s} \\ 0 & \text { else }\end{array}\right.
p ( t ) = ⎩ ⎨ ⎧ 2 + 2 t / T s 2 − 2 t / T s 0 − T s ≤ t < 0 0 ≤ t < T s else
旁瓣较高
Cosine pulses(余弦脉冲)
p ( t ) = sin π t T s p(t)=\sin\frac{\pi t}{T_s}
p ( t ) = sin T s π t
旁瓣比矩形脉冲低10 dB
Raised Cosine Pulses(升余弦脉冲)
频域
P ( f ) = { T s 0 ≤ ∣ f ∣ ≤ ( 1 − β ) / 2 T s T s 2 [ 1 − sin π T s β ( f − 1 2 T s ) ] ( 1 − β ) / 2 T s ≤ ∣ f ∣ ≤ ( 1 + β ) / 2 T s P(f)=\left\{\begin{array}{ll}T_{s} & 0 \leq|f| \leq(1-\beta) / 2 T_{s} \\ \frac{T_{s}}{2}\left[1-\sin \frac{\pi T_{s}}{\beta}\left(f-\frac{1}{2 T_{s}}\right)\right] & (1-\beta) / 2 T_{s} \leq|f| \leq(1+\beta) / 2 T_{s}\end{array}\right.
P ( f ) = { T s 2 T s [ 1 − sin β π T s ( f − 2 T s 1 ) ] 0 ≤ ∣ f ∣ ≤ ( 1 − β ) / 2 T s ( 1 − β ) / 2 T s ≤ ∣ f ∣ ≤ ( 1 + β ) / 2 T s
时域
p ( t ) = sin π t / T s π t / T s cos β π t / T s 1 − 4 β 2 t 2 / T s 2 p(t)=\frac{\sin \pi t / T_s}{\pi t / T_s} \frac{\cos \beta \pi t / T_s}{1-4 \beta^2 t^2 / T_s^2}
p ( t ) = π t / T s sin π t / T s 1 − 4 β 2 t 2 / T s 2 cos β π t / T s
升余弦序列拖尾衰减很快,ISI小
码元同步(Symbol Synchronization):需要通过码元同步来划定与特定符号相关的接收信号。
载波同步(Carrier Phase Recovery):得到相位信息。
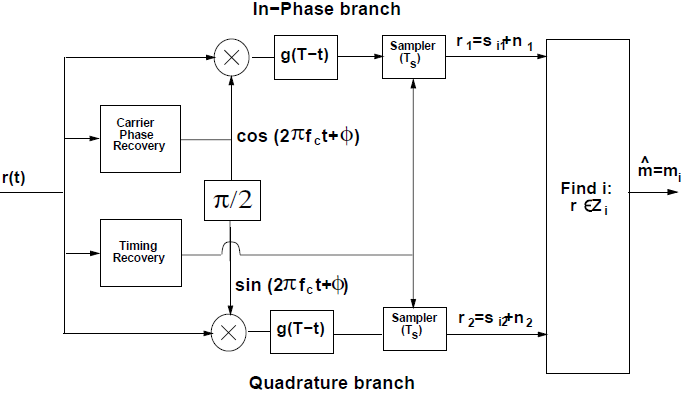
接收机形式
接收信号
r ( t ) = ℜ { ( x ( t − τ ) e j ϕ + z ( t ) ) e j 2 π f c t } r(t)=\Re\left\{\left(x(t-\tau) e^{j \phi}+z(t)\right) e^{j 2 \pi f_{c} t}\right\}
r ( t ) = ℜ { ( x ( t − τ ) e j ϕ + z ( t ) ) e j 2 π f c t }
码元同步需要估计τ \tau τ ϕ \phi ϕ θ = ( ϕ , τ ) \theta=(\phi,\tau) θ = ( ϕ , τ )
r ( t ) = s ( t ; θ ) + n ( t ) r(t)=s(t;\theta)+n(t)
r ( t ) = s ( t ; θ ) + n ( t )
最大似然估计(the maximum-likelhood criterion, ML)
max p ( r ∣ θ ) = ( 1 π N 0 σ ) K exp [ − ∑ k = 1 K ( r k − s k ( θ ) ) 2 N 0 ] \max p(\mathbf{r} \mid \theta)=\left(\frac{1}{\sqrt{\pi N_{0}} \sigma}\right)^{K} \exp \left[-\sum_{k=1}^{K} \frac{\left(r_{k}-s_{k}(\theta)\right)^{2}}{N_{0}}\right]
max p ( r ∣ θ ) = ( π N 0 σ 1 ) K exp [ − k = 1 ∑ K N 0 ( r k − s k ( θ ) ) 2 ]
似然函数(likelihood function)
Λ ( θ ) = exp [ − 1 N 0 ∫ T 0 [ r ( t ) − s ( t ; θ ) ] 2 ] d t \Lambda(\theta)=\exp \left[-\frac{1}{N_{0}} \int_{T_{0}}[r(t)-s(t ; \theta)]^{2}\right] d t
Λ ( θ ) = exp [ − N 0 1 ∫ T 0 [ r ( t ) − s ( t ; θ ) ] 2 ] d t
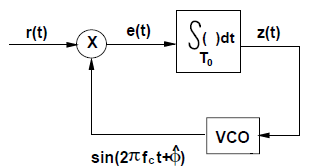
最大似然相位估计(Maximum Likelihood Phase Estimation)
ϕ ^ = − arctan [ ∫ T 0 r ( t ) sin ( 2 π f c t ) d t ∫ T 0 r ( t ) cos ( 2 π f c t ) d t ] \hat{\phi}=-\arctan \left[\frac{\int_{T_{0}} r(t) \sin \left(2 \pi f_{c} t\right) d t}{\int_{T_{0}} r(t) \cos \left(2 \pi f_{c} t\right) d t}\right]
ϕ ^ = − arctan [ ∫ T 0 r ( t ) cos ( 2 π f c t ) d t ∫ T 0 r ( t ) sin ( 2 π f c t ) d t ]
实现方法——锁相环(phase lock loop)
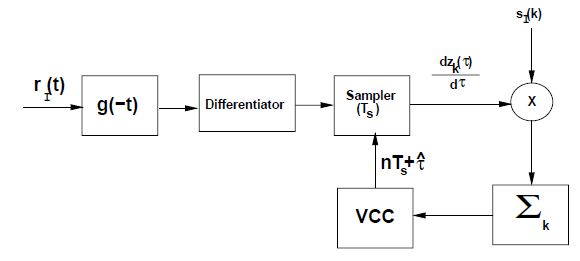
最大似然定时估计(Maximum Likelihood Timing Estimation)
∑ k s I ( k ) ∂ ∂ τ z k ( τ ) = 0 \sum_{k} s_{I}(k) \frac{\partial}{\partial \tau} z_{k}(\tau)=0
k ∑ s I ( k ) ∂ τ ∂ z k ( τ ) = 0
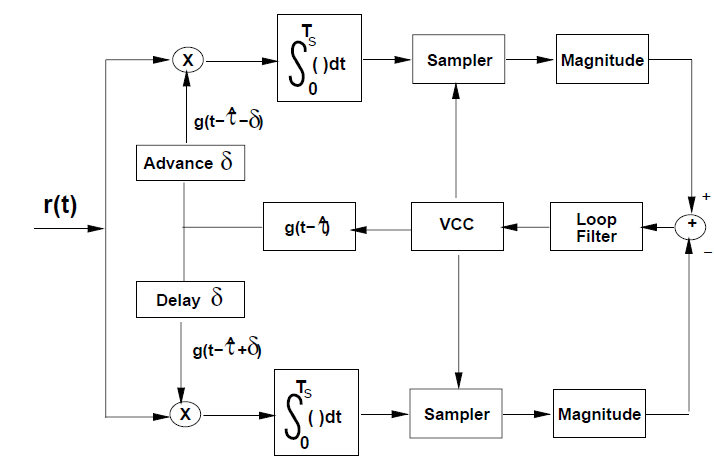
decision-directed estimation(非盲估计): voltage-controlled clock (VCC)
non decision-directed timing estimation(盲估计):early-late gate synchronizer(超前滞后门)
接收信噪比(received SNR)
S N R = P r N 0 B \mathrm{SNR}=\frac{P_r}{N_0B}
S N R = N 0 B P r
接收功率P r P_r P r P t P_t P t
噪声功率取决于s ( t ) s(t) s ( t ) s ( t ) s(t) s ( t ) B B B 2 B 2B 2 B N 0 2 \frac{N_0}{2} 2 N 0 N = N 0 2 2 B = N 0 B N=\frac{N_0}{2}2B=N_0B N = 2 N 0 2 B = N 0 B
接收信-干-噪比(received signal-to-interference-plus-noise power ratio, SINR)
S I N R = P r N 0 + P I \mathrm{SINR}=\frac{P_r}{N_0+P_I}
S I N R = N 0 + P I P r
信噪比的能量表示
S N R = P r N 0 B = E s N 0 B T s = E b N 0 B T b \mathrm{SNR}=\frac{P_r}{N_0B}=\frac{E_s}{N_0BT_s}=\frac{E_b}{N_0BT_b}
S N R = N 0 B P r = N 0 B T s E s = N 0 B T b E b
其中,T s T_s T s T b T_b T b
符号信噪比(SNR per symbol)与比特信噪比(SNR per bit)
符号信噪比
γ s = E s N 0 \gamma_s=\frac{E_s}{N_0}
γ s = N 0 E s
比特信噪比
γ b = E b N 0 \gamma_b=\frac{E_b}{N_0}
γ b = N 0 E b
对于任意成形脉冲满足T s = k B T_s=\frac{k}{B} T s = B k
k × S N R = E s N 0 = γ s k\times \mathrm{SNR}=\frac{E_s}{N_0}=\gamma_s
k × S N R = N 0 E s = γ s
误码率:
P e = ∑ i = 1 M p ( r ∉ Z i ∣ 发射序列为 m i ) p ( 发射序列为 m i ) = 1 − 1 M ∑ i = 1 M ∫ Z i − s i p ( n ) d n \begin{aligned}
P_e=&\sum_{i=1}^Mp(\mathbf{r}\notin Z_i|\text{发射序列为}m_i)p(\text{发射序列为}m_i)\\
=&1-\frac 1M\sum_{i=1}^M\int_{Z_i-\mathbf{s}_i}p(\mathbf{n})d\mathbf{n}
\end{aligned}
P e = = i = 1 ∑ M p ( r ∈ / Z i ∣ 发射序列为 m i ) p ( 发射序列为 m i ) 1 − M 1 i = 1 ∑ M ∫ Z i − s i p ( n ) d n
形象地理解错误率就是星座点s i \mathbf{s}_i s i s i + n \mathbf{s}_i+\mathbf{n} s i + n Z i Z_i Z i
错误率积分具有平移不变性和旋转不变性
利用联合界(Union bound)描述错误概率:
用联合界表示发射序列为m i m_i m i
P e ( 发射序列为 m i ) = p ( ⋃ k = 1 k ≠ i M A i k ) ≤ ∑ k = 1 k ≠ i M p ( A i k ) P_{e}\left( \text {发射序列为 }m_{i}\right)=p\left(\bigcup_{k=1 \atop k \neq i}^{M} A_{i k}\right) \leq \sum_{k=1 \atop k \neq i}^{M} p\left(A_{i k}\right)
P e ( 发射序列为 m i ) = p ⎝ ⎜ ⎛ k = i k = 1 ⋃ M A i k ⎠ ⎟ ⎞ ≤ k = i k = 1 ∑ M p ( A i k )
其中,A i k A_{ik} A i k s i \mathbf{s}_i s i ∥ r − s k ∥ < ∥ r − s i ∥ \left\|\mathbf{r}-\mathbf{s}_{k}\right\|<\left\|\mathbf{r}-\mathbf{s}_{i}\right\| ∥ r − s k ∥ < ∥ r − s i ∥
经过化简可以发现错判概率等于噪声向量n \mathbf{n} n s i − s k \mathbf{s}_i-\mathbf{s}_k s i − s k
误码率的界:
联合界估计的界 :
P e = ∑ i = 1 M p ( m i ) P e ( 发射序列为 m i ) ≤ 1 M ∑ i = 1 M ∑ k = 1 k ≠ i M Q ( d i k 2 N 0 ) P_{e}=\sum_{i=1}^{M} p\left(m_{i}\right) P_{e}(\text {发射序列为 }m_{i}) \leq \frac{1}{M} \sum_{i=1}^{M} \sum_{k=1 \atop k \neq i}^{M} Q\left(\frac{d_{i k}}{\sqrt{2 N_{0}}}\right)
P e = i = 1 ∑ M p ( m i ) P e ( 发射序列为 m i ) ≤ M 1 i = 1 ∑ M k = i k = 1 ∑ M Q ( 2 N 0 d i k )
其中,Q函数为
Q ( z ) = ∫ z ∞ 1 2 π e − x 2 2 d x = 1 2 e r f c ( z 2 ) Q(z)=\int_z^\infty \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\mathrm{d}x=\frac 12\mathrm{erfc}\left(\frac{z}{\sqrt{2}}\right)
Q ( z ) = ∫ z ∞ 2 π 1 e − 2 x 2 d x = 2 1 e r f c ( 2 z )
利用最小距离估计的界 :
P e ≤ ( M − 1 ) Q ( d min 2 N 0 ) = M − 1 π exp [ − d min 2 4 N 0 ] P_{e} \leq(M-1) Q\left(\frac{d_{\min }}{\sqrt{2 N_{0}}}\right)= \frac{M-1}{\sqrt{\pi}} \exp \left[\frac{-d_{\min }^{2}}{4 N_{0}}\right]
P e ≤ ( M − 1 ) Q ( 2 N 0 d min ) = π M − 1 exp [ 4 N 0 − d min 2 ]
其中,最小距离(minimum distance)为d min = min i , k d i k = min i , k ∣ ∣ s i − s k ∣ ∣ d_{\min}=\min_{i,k}d_{ik}=\min_{i,k}||\mathbf{s}_i-\mathbf{s}_k|| d min = min i , k d i k = min i , k ∣ ∣ s i − s k ∣ ∣
最近邻近似(the nearest neighbor approximation)
P e ≈ M d min Q ( d min 2 N 0 ) P_{e} \approx M_{d_{\min }} Q\left(\frac{d_{\min }}{\sqrt{2 N_{0}}}\right)
P e ≈ M d min Q ( 2 N 0 d min )
其中,M d min M_{d_{\min}} M d min d min d_{\min} d min
最近邻近似小于最小距离估计的界,略小于联合界估计的界
在高信噪比情况下,最近邻近似解接近误码率的准确值
最近邻近似仅取决于最小距离d min d_{\min} d min M d min M_{d_{\min}} M d min
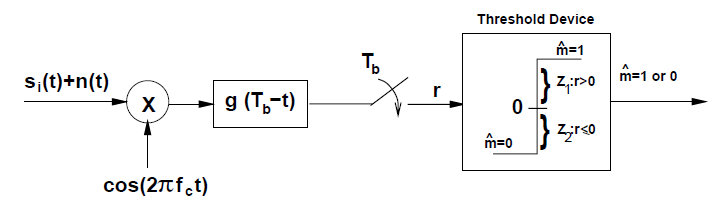
对于M = 2 M=2 M = 2
P b = P s = Q ( d min 2 N 0 ) P_b=P_s=Q\left(\frac{d_{\min}}{\sqrt{2N_0}}\right)
P b = P s = Q ( 2 N 0 d min )
误码率与误信率
误码率(误符号率,symbol error probability,P e , P s P_e,P_s P e , P s
误信率(误比特率,bit error probability,P b P_b P b
对于Gray encoding,高信噪比时可以认为一码元错误对应一比特错误,则
P b ≈ P s log 2 M P_b\approx\frac{P_s}{\log_2M}
P b ≈ log 2 M P s
Q函数表现形式
形式一:
Q ( z ) = ∫ z ∞ 1 2 π e − x 2 2 d x = 1 2 e r f c ( z 2 ) Q(z)=\int_z^\infty \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\mathrm{d}x=\frac 12\mathrm{erfc}\left(\frac{z}{\sqrt{2}}\right)
Q ( z ) = ∫ z ∞ 2 π 1 e − 2 x 2 d x = 2 1 e r f c ( 2 z )
形式二:
Q ( z ) = 1 π ∫ 0 π / 2 exp [ − z 2 2 sin 2 ϕ ] d ϕ ( z > 0 ) Q(z)=\frac{1}{\pi} \int_{0}^{\pi / 2} \exp \left[\frac{-z^{2}}{2 \sin ^{2} \phi}\right] d \phi \quad (z>0)
Q ( z ) = π 1 ∫ 0 π / 2 exp [ 2 sin 2 ϕ − z 2 ] d ϕ ( z > 0 )
注意到形式一积分区间为无穷,函数变量z z z z z z
2PSK的误比特率(注意对于M = 2 M=2 M = 2
P b = Q ( d min 2 N 0 ) = Q ( 2 E b 2 N 0 ) = Q ( 2 γ b ) P_b=Q\left(\frac{d_{\min}}{\sqrt{2N_0}}\right)=Q\left(\frac{2\sqrt{E_b}}{\sqrt{2N_0}}\right)=Q\left(\sqrt{2\gamma_b}\right)
P b = Q ( 2 N 0 d min ) = Q ( 2 N 0 2 E b ) = Q ( 2 γ b )
QPSK的误码率与误比特率
QPSK的同相和正交分量都是2PSK
误码率
P s = 1 − [ 1 − Q ( 2 γ b ) ] 2 = 1 − [ 1 − Q ( γ s ) ] 2 P_s=1-\left[1-Q\left(\sqrt{2\gamma_b}\right)\right]^2=1-\left[1-Q\left(\sqrt{\gamma_s}\right)\right]^2
P s = 1 − [ 1 − Q ( 2 γ b ) ] 2 = 1 − [ 1 − Q ( γ s ) ] 2
误码率的最近邻近似
P s = 2 Q ( A 2 N 0 ) = 2 Q ( γ s 2 ) P_s=2Q\left(\frac{A^2}{N_0}\right)=2Q\left(\sqrt{\frac{\gamma_s}{2}}\right)
P s = 2 Q ( N 0 A 2 ) = 2 Q ( 2 γ s )
根据格雷码映射,误比特率为
P b ≈ P s 2 = Q ( γ s 2 ) P_b\approx \frac{P_s}{2}=Q\left(\sqrt{\frac{\gamma_s}{2}}\right)
P b ≈ 2 P s = Q ( 2 γ s )
MPSK的误码率
误码率的最近邻近似——近邻d min = 2 A sin ( π M ) d_{\min}=2A\sin\left(\frac{\pi}{M}\right) d min = 2 A sin ( M π )
P s ≈ 2 Q ( 2 A sin ( π M ) 2 N 0 ) = 2 Q ( 2 γ s sin ( π M ) ) P_s\approx2Q\left(\frac{2A\sin\left(\frac{\pi}{M}\right)}{\sqrt{2N_0}}\right)=2Q\left(\sqrt{2\gamma_s}\sin\left(\frac{\pi}{M}\right)\right)
P s ≈ 2 Q ( 2 N 0 2 A sin ( M π ) ) = 2 Q ( 2 γ s sin ( M π ) )
通过同相和正交支路噪声的联合分布得到γ , θ \gamma,\theta γ , θ γ \gamma γ
P s = 1 − ∫ − π / M π / M 1 π e − 2 γ s sin 2 ( θ ) ∫ 0 ∞ z exp [ − ( z − 2 γ s cos ( θ ) ) 2 ] d z P_{s}=1-\int_{-\pi / M}^{\pi / M} \frac{1}{\pi} e^{-2 \gamma_{s} \sin ^{2}(\theta)} \int_{0}^{\infty} z \exp \left[-\left(z-\sqrt{2 \gamma_{s}} \cos (\theta)\right)^{2}\right] d z
P s = 1 − ∫ − π / M π / M π 1 e − 2 γ s sin 2 ( θ ) ∫ 0 ∞ z exp [ − ( z − 2 γ s cos ( θ ) ) 2 ] d z
但M > 4 M>4 M > 4
MPSK对于相位误差敏感,但相位误差很大是会带来error floor
MPAM的误码率
P s = 2 ( M − 1 ) M Q ( 6 γ ˉ s M 2 − 1 ) P_{s}=\frac{2(M-1)}{M} Q\left(\sqrt{\frac{6 \bar{\gamma}_{s}}{M^{2}-1}}\right)
P s = M 2 ( M − 1 ) Q ( M 2 − 1 6 γ ˉ s )
MQAM的误码率
M = L 2 M=L^2 M = L 2
P s = 1 − ( 1 − 2 ( M − 1 ) M Q ( 3 γ ˉ s M − 1 ) ) 2 P P_{s}=1-\left(1-\frac{2(\sqrt{M}-1)}{\sqrt{M}} Q\left(\sqrt{\frac{3 \bar{\gamma}_{s}}{M-1}}\right)\right)^{2}P
P s = 1 − ( 1 − M 2 ( M − 1 ) Q ( M − 1 3 γ ˉ s ) ) 2 P
最近邻近似(正方形星座)
英文原版——用两支路MPAM来近似(偏小)
P s = 2 ( M − 1 ) M Q ( 3 γ ˉ s M − 1 ) P_s=\frac{2(\sqrt{M}-1)}{\sqrt{M}} Q\left(\sqrt{\frac{3 \bar{\gamma}_{s}}{M-1}}\right)
P s = M 2 ( M − 1 ) Q ( M − 1 3 γ ˉ s )
中文翻译版——假设内点外点都有4个距离为2 d 2d 2 d
P s = 4 Q ( 3 γ ˉ s M − 1 ) P_s=4 Q\left(\sqrt{\frac{3 \bar{\gamma}_{s}}{M-1}}\right)
P s = 4 Q ( M − 1 3 γ ˉ s )
最近邻近似(非正方形星座)
P s ≈ M d min Q ( d min 2 N 0 ) P_{s} \approx M_{d_{\min }} Q\left(\frac{d_{\min }}{\sqrt{2 N_{0}}}\right)
P s ≈ M d min Q ( 2 N 0 d min )
For the same energy per symbol or bit, MQAM makes more efficient use of energy and thus has better performance.
MQAM解调需要对幅度和相位两方面进行估计
相位估计与MPSK类似
幅度估计可以使用AGC(自动增益控制)
2FSK的误比特率:
P b = P s = Q ( A N 0 ) = Q ( γ b ) P_b=P_s=Q\left(\frac{A}{\sqrt{N_0}}\right)=Q\left(\sqrt{\gamma_b}\right)
P b = P s = Q ( N 0 A ) = Q ( γ b )
MFSK的误码率:
P s = ∑ m = 1 M ( − 1 ) m + 1 C M − 1 m 1 m + 1 exp [ − m γ s m + 1 ] P_{s}=\sum_{m=1}^{M}(-1)^{m+1}\mathbf{C}_{M-1}^{m} \frac{1}{m+1} \exp \left[\frac{-m \gamma_{s}}{m+1}\right]
P s = m = 1 ∑ M ( − 1 ) m + 1 C M − 1 m m + 1 1 exp [ m + 1 − m γ s ]
CPFSK的错误率取决于检波器是相干的还是非相干的,也取决于它是使用逐码元检测还是序列估计。
误码率的近似
P s ( γ s ) ≈ α M Q ( β M γ s ) P_s(\gamma_s)\approx\alpha_MQ\left(\sqrt{\beta_M\gamma_s}\right)
P s ( γ s ) ≈ α M Q ( β M γ s )
对于最近邻近似,α M = M d min \alpha_M=M_{d_{\min}} α M = M d min β M \beta_M β M d min d_{\min} d min
误比特率的近似
P b ( γ b ) = α M log 2 M Q ( log 2 M β M γ b ) P_b(\gamma_b)=\frac{\alpha_M}{\log_2M}Q\left(\sqrt{\frac{\log_2M}{\beta_M}\gamma_b}\right)
P b ( γ b ) = log 2 M α M Q ( β M log 2 M γ b )
Modulation P s ( γ s ) P b ( γ b ) 2FSK: P b = Q ( γ b ) 2PSK: P b = Q ( 2 γ b ) QPSK,4QAM: P s ≈ 2 Q ( γ s ) P b ≈ Q ( 2 γ b ) MPAM: P s ≈ 2 ( M − 1 ) M Q ( 6 γ ˉ s M 2 − 1 ) P b ≈ 2 ( M − 1 ) M log 2 M Q ( 6 γ ˉ b log 2 M M 2 − 1 ) MPSK: P s ≈ 2 Q ( 2 γ s sin ( π M ) ) P b ≈ 2 log 2 M Q ( 2 γ b log 2 M sin ( π M ) ) Rectangular MQAM: P s ≈ 4 ( M − 1 ) M Q ( 3 γ ˉ s M − 1 ) P b ≈ 4 ( M − 1 ) M log 2 M Q ( 3 γ ˉ b log 2 M ( M − 1 ) ) Nonrectangular MQAM: P s ≈ 4 Q ( 3 γ ˉ s M − 1 ) P b ≈ 4 log 2 M Q ( 3 γ ˉ b log 2 M ( M − 1 ) ) \begin{array}{|c|c|c|}
\hline \text { Modulation } & P_{s}\left(\gamma_{s}\right) & P_{b}\left(\gamma_{b}\right) \\
\hline \text { 2FSK: } & & P_{b}=Q\left(\sqrt{\gamma_{b}}\right) \\
\hline \text { 2PSK: } & & P_{b}=Q\left(\sqrt{2 \gamma_{b}}\right) \\
\hline \text { QPSK,4QAM: } & P_{s} \approx 2 Q\left(\sqrt{\gamma_{s}}\right) & P_{b} \approx Q\left(\sqrt{2 \gamma_{b}}\right) \\
\hline \text { MPAM: } & P_{s} \approx \frac{2(M-1)}{M} Q\left(\sqrt{\frac{6 \bar{\gamma}_{s}}{M^{2}-1}}\right) & P_{b} \approx \frac{2(M-1)}{M \log _{2} M} Q\left(\sqrt{\frac{6 \bar{\gamma}_{b} \log _{2} M}{M^{2}-1}}\right) \\
\hline \text { MPSK: } & P_{s} \approx 2 Q\left(\sqrt{2 \gamma_{s}} \sin \left(\frac {\pi}{M}\right)\right) & P_{b} \approx \frac{2}{\log _{2} M} Q\left(\sqrt{2 \gamma_{b} \log _{2} M} \sin \left(\frac {\pi}{M}\right)\right) \\
\hline \text { Rectangular MQAM: } & P_{s} \approx \frac{4(\sqrt{M}-1)}{\sqrt{M}} Q\left(\sqrt{\frac{3 \bar{\gamma}_{s}}{M-1}}\right) & P_{b} \approx \frac{4(\sqrt{M}-1)}{\sqrt{M} \log _{2} M} Q\left(\sqrt{\frac{3 \bar{\gamma}_{b} \log _{2} M}{(M-1)}}\right) \\
\hline \text { Nonrectangular MQAM: } & P_{s} \approx 4 Q\left(\sqrt{\frac{3 \bar{\gamma}_{s}}{M-1}}\right) & P_{b} \approx \frac{4}{\log _{2} M} Q\left(\sqrt{\frac{3 \bar{\gamma}_{b} \log _{2} M}{(M-1)}}\right) \\
\hline
\end{array}
Modulation 2FSK: 2PSK: QPSK,4QAM: MPAM: MPSK: Rectangular MQAM: Nonrectangular MQAM: P s ( γ s ) P s ≈ 2 Q ( γ s ) P s ≈ M 2 ( M − 1 ) Q ( M 2 − 1 6 γ ˉ s ) P s ≈ 2 Q ( 2 γ s sin ( M π ) ) P s ≈ M 4 ( M − 1 ) Q ( M − 1 3 γ ˉ s ) P s ≈ 4 Q ( M − 1 3 γ ˉ s ) P b ( γ b ) P b = Q ( γ b ) P b = Q ( 2 γ b ) P b ≈ Q ( 2 γ b ) P b ≈ M log 2 M 2 ( M − 1 ) Q ( M 2 − 1 6 γ ˉ b log 2 M ) P b ≈ log 2 M 2 Q ( 2 γ b log 2 M sin ( M π ) ) P b ≈ M log 2 M 4 ( M − 1 ) Q ( ( M − 1 ) 3 γ ˉ b log 2 M ) P b ≈ log 2 M 4 Q ( ( M − 1 ) 3 γ ˉ b log 2 M )
中文版在矩形MQAM中有一些区别,没有4 ( M − 1 ) M \frac{4(\sqrt{M}-1)}{\sqrt{M}} M 4 ( M − 1 )
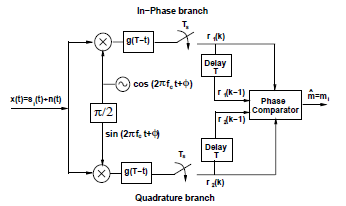
差分解调利用相位比较器求得相位,进行抽样判决。
Performance of differential modulation that is roughly 3 dB worse than that of coherent modulation.
DPSK的误比特率:
P b = 1 2 e − γ b P_b=\frac 12 e^{-\gamma_b}
P b = 2 1 e − γ b
DQPSK的误比特率:
P b ≈ ∫ b ∞ x exp ( − ( a 2 + x 2 ) 2 ) I 0 ( a x ) d x − 1 2 exp ( − ( a 2 + b 2 ) 2 ) I 0 ( a b ) P_{b} \approx \int_{b}^{\infty} x \exp \left(\frac{-\left(a^{2}+x^{2}\right)}{2}\right) \mathrm{I}_{0}(a x) d x-\frac{1}{2} \exp \left(\frac{-\left(a^{2}+b^{2}\right)}{2}\right) \mathrm{I}_{0}(a b)
P b ≈ ∫ b ∞ x exp ( 2 − ( a 2 + x 2 ) ) I 0 ( a x ) d x − 2 1 exp ( 2 − ( a 2 + b 2 ) ) I 0 ( a b )
其中, a ≈ 0.765 γ b a \approx 0.765 \sqrt{\gamma_{b}} a ≈ 0 . 7 6 5 γ b b ≈ 1.85 γ b b \approx 1.85 \sqrt{\gamma_{b}} b ≈ 1 . 8 5 γ b I 0 ( x ) I_0(x) I 0 ( x )
性能指标的选取取决于衰落信道变换快慢:
中断率P o u t P_{out} P o u t T c ≫ T s T_c\gg T_s T c ≫ T s
平均错误率P ˉ s \bar P_s P ˉ s T c ≈ T s T_c\approx T_s T c ≈ T s
中断率和平均错误率的结合:信道衰落快慢结合,例如慢变对数正态分布的shadowing和快变Rayleigh衰落。
信道衰落非常快(T c ≪ T s T_c\ll T_s T c ≪ T s
中断率(Outage Probability)的定义
P o u t = p ( γ < γ 0 ) = ∫ 0 γ 0 p γ s ( γ ) d γ P_{out}=p(\gamma<\gamma_0)=\int_0^{\gamma_0}p_{\gamma_s}(\gamma)\ \mathrm{d}\gamma
P o u t = p ( γ < γ 0 ) = ∫ 0 γ 0 p γ s ( γ ) d γ
其中,γ 0 \gamma_0 γ 0
瑞利信道的中断率
中断率
P o u t = ∫ 0 γ 0 1 γ ˉ s e − γ s γ ˉ s d γ s = 1 − e − γ 0 γ ˉ s P_{out}=\int_0^{\gamma_0}\frac{1}{\bar \gamma_s}e^{-\frac{\gamma_s}{\bar \gamma_s}}d\gamma_s=1-e^{-\frac{\gamma_0}{\bar\gamma_s}}
P o u t = ∫ 0 γ 0 γ ˉ s 1 e − γ ˉ s γ s d γ s = 1 − e − γ ˉ s γ 0
对应所需的平均信噪比
γ ˉ s = γ 0 − ln ( 1 − P o u t ) \bar \gamma_s=\frac{\gamma_0}{-\ln(1-P_{out})}
γ ˉ s = − ln ( 1 − P o u t ) γ 0
dB fade margin(分贝衰落余量):
F d = − log [ − ln ( 1 − P o u t ) ] F_d=-\log[-\ln(1-P_{out})]
F d = − log [ − ln ( 1 − P o u t ) ]
平均误码率:根据衰落的分布对AWGN信道的误码率积分。
P ˉ s = ∫ 0 ∞ P s ( γ ) p γ s ( γ ) d γ \bar P_s=\int_0^\infty P_s(\gamma)p_{\gamma_s}(\gamma)\mathrm{d}\gamma
P ˉ s = ∫ 0 ∞ P s ( γ ) p γ s ( γ ) d γ
p γ s ( γ ) p_{\gamma_s}(\gamma) p γ s ( γ )
p γ s ( γ ) d γ = p ( r ) d r p_{\gamma_s}(\gamma)d\gamma=p(r)dr
p γ s ( γ ) d γ = p ( r ) d r
瑞利衰落的分布
p γ s ( γ ) = 1 γ s ˉ exp ( − γ γ ˉ s ) p_{\gamma_s}(\gamma)=\frac{1}{\bar{\gamma_s}}\exp\left(-\frac{\gamma}{\bar \gamma_s}\right)
p γ s ( γ ) = γ s ˉ 1 exp ( − γ ˉ s γ )
其中,γ ˉ s = σ 2 T σ n 2 \bar \gamma_s=\frac{\sigma^2T}{\sigma_n^2} γ ˉ s = σ n 2 σ 2 T
瑞利信道中二元调制的平均误码率
2PSK
P ˉ b = 1 2 [ 1 − γ ˉ b 1 + γ ˉ b ] ≈ 1 4 γ ˉ b \bar{P}_{b}=\frac{1}{2}\left[1-\sqrt{\frac{\bar{\gamma}_{b}}{1+\bar{\gamma}_{b}}}\right] \approx \frac{1}{4 \bar{\gamma}_{b}}
P ˉ b = 2 1 [ 1 − 1 + γ ˉ b γ ˉ b ] ≈ 4 γ ˉ b 1
2FSK
P ˉ b = 1 2 [ 1 − γ ˉ b 2 + γ ˉ b ] ≈ 1 4 γ ˉ b \bar{P}_{b}=\frac{1}{2}\left[1-\sqrt{\frac{\bar{\gamma}_{b}}{2+\bar{\gamma}_{b}}}\right] \approx \frac{1}{4 \bar{\gamma}_{b}}
P ˉ b = 2 1 [ 1 − 2 + γ ˉ b γ ˉ b ] ≈ 4 γ ˉ b 1
2DPSK
P ˉ b = 1 2 ( 1 + γ ˉ b ) ≈ 1 2 γ ˉ b \bar{P}_{b}=\frac{1}{2\left(1+\bar{\gamma}_{b}\right)} \approx \frac{1}{2 \bar{\gamma}_{b}}
P ˉ b = 2 ( 1 + γ ˉ b ) 1 ≈ 2 γ ˉ b 1
约等号仅当γ ˉ b \bar\gamma_b γ ˉ b
通用近似式P s ( γ s ) ≈ α M Q ( β M γ s ) P_s(\gamma_s)\approx\alpha_MQ\left(\sqrt{\beta_M\gamma_s}\right) P s ( γ s ) ≈ α M Q ( β M γ s )
P ˉ s ≈ ∫ 0 ∞ α M Q ( β M γ ) ⋅ 1 γ ˉ s e − γ / γ ˉ s d γ s = α m 2 [ 1 − 0.5 β M γ ˉ s 1 + 0.5 β M γ ˉ s ] ≈ α M 2 β M γ ˉ s \bar{P}_{s} \approx \int_{0}^{\infty} \alpha_{M} Q\left(\sqrt{\beta_{M} \gamma}\right) \cdot \frac{1}{\bar{\gamma}_{s}} e^{-\gamma / \bar{\gamma}_{s}} d \gamma_{s}=\frac{\alpha_{m}}{2}\left[1-\sqrt{\frac{0.5 \beta_{M} \bar{\gamma}_{s}}{1+0.5 \beta_{M} \bar{\gamma}_{s}}}\right] \approx \frac{\alpha_{M}}{2 \beta_{M} \bar{\gamma}_{s}}
P ˉ s ≈ ∫ 0 ∞ α M Q ( β M γ ) ⋅ γ ˉ s 1 e − γ / γ ˉ s d γ s = 2 α m [ 1 − 1 + 0 . 5 β M γ ˉ s 0 . 5 β M γ ˉ s ] ≈ 2 β M γ ˉ s α M
AWGN信道与衰落信道中调制方式的比较
在AWGN信道中,误比特率随着γ b \gamma_b γ b 指数级下降 。在衰落信道中,所有调制类型的误比特率随着γ b \gamma_b γ b 线性下降 。同样误码率条件下,衰落信道中需要更高的信噪比。
瑞利衰落是最差的衰落情况。Nakagami fading随m m m
Moment Generating Function(矩函数产生函数,矩母函数)
M γ ( s ) = ∫ 0 ∞ p γ ( γ ) e s γ d γ \mathcal{M}_{\gamma}(s)=\int_{0}^{\infty} p_{\gamma}(\gamma) e^{s \gamma} d \gamma
M γ ( s ) = ∫ 0 ∞ p γ ( γ ) e s γ d γ
其实这里的矩母函数类似于《随机信号分析》中的特征函数,其实在第七章分集中也谈到了用j λ j\lambda j λ s s s
特征函数
φ x ( λ , t ) = ∫ − ∞ ∞ p ( x , t ) e j λ x d x \varphi_x(\lambda,t )=\int_{-\infty}^{\infty}p(x,t)e^{j\lambda x}\mathrm{d}x
φ x ( λ , t ) = ∫ − ∞ ∞ p ( x , t ) e j λ x d x
用特征函数求各阶矩
E [ X n ( t ) ] = ( − j ) n ∂ n ∂ λ n φ x ( λ , t ) ∣ λ = 0 E[X^n(t)]=(-j)^n\left.\frac{\partial^n}{\partial \lambda^n}\varphi_x(\lambda,t)\right|_{\lambda=0}
E [ X n ( t ) ] = ( − j ) n ∂ λ n ∂ n φ x ( λ , t ) ∣ ∣ ∣ ∣ λ = 0
用Moment Generating Function求平均误码率
相关解调误码率的近似(α = α M , g = β M 2 \alpha=\alpha_M,g=\frac{\beta_M}{2} α = α M , g = 2 β M
P s ( γ s ) ≈ α Q ( 2 g γ s ) = α π ∫ 0 π 2 exp ( − g γ sin 2 ϕ ) d ϕ \begin{aligned}
P_s(\gamma_s)\approx&\alpha Q\left(\sqrt{2g\gamma_s}\right)\\
=&\frac{\alpha}{\pi}\int_0^{\frac \pi2}\exp\left(\frac{-g\gamma}{\sin^2\phi}\right)\mathrm{d}\phi
\end{aligned}
P s ( γ s ) ≈ = α Q ( 2 g γ s ) π α ∫ 0 2 π exp ( sin 2 ϕ − g γ ) d ϕ
衰落信道的平均误码率
P ˉ s = α π ∫ 0 π 2 M γ s ( − g sin 2 ϕ ) d ϕ \bar P_s=\frac{\alpha}{\pi} \int_{0}^{\frac \pi 2} \mathcal{M}_{\gamma_{s}}\left(\frac{-g}{\sin ^{2} \phi}\right) d \phi
P ˉ s = π α ∫ 0 2 π M γ s ( sin 2 ϕ − g ) d ϕ
Let γ s ˉ ˉ \bar{\bar {\gamma_s}} γ s ˉ ˉ
Let γ ˉ s \bar \gamma_s γ ˉ s γ s ˉ ˉ \bar{\bar {\gamma_s}} γ s ˉ ˉ
Let γ s \gamma_s γ s
P ˉ s = ∫ 0 ∞ P s ( γ s ) p ( γ s ∣ γ ˉ s ) d γ s \bar{P}_{s}=\int_{0}^{\infty} P_{s}\left(\gamma_{s}\right) p\left(\gamma_{s} \mid \bar{\gamma}_{s}\right) d \gamma_{s}
P ˉ s = ∫ 0 ∞ P s ( γ s ) p ( γ s ∣ γ ˉ s ) d γ s
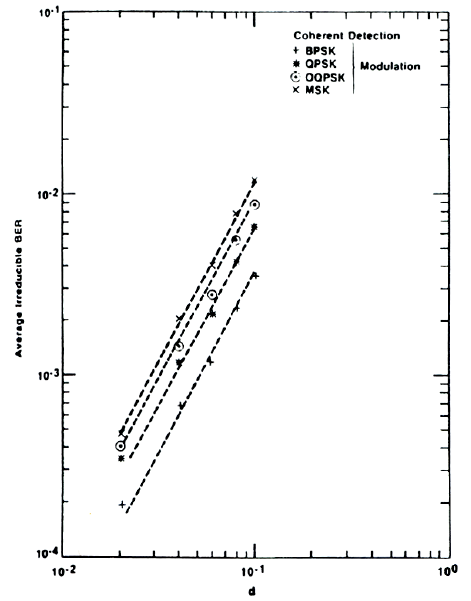
多普勒频移扩展会使得差分编码在解调时出现不可避免地error floor。码元之间的相位相关性以及因此而产生的性能下降是多普勒频率f D = v λ f_D=\frac{v}{\lambda} f D = λ v T s T_s T s
2DPSK的error floor
P ˉ floor = ( 1 − ρ C ) e − K 2 \bar{P}_{\text {floor }}=\frac{\left(1-\rho_{C}\right) e^{-K}}{2}
P ˉ floor = 2 ( 1 − ρ C ) e − K
DQPSK的error floor
P ˉ floor = 1 2 [ 1 − ( ρ C / 2 ) 2 1 − ( ρ C / 2 ) 2 ] exp [ − ( 2 − 2 ) ( K / 2 ) 1 − ρ C / 2 ] \bar{P}_{\text {floor }}=\frac{1}{2}\left[1-\sqrt{\frac{\left(\rho_{C} / \sqrt{2}\right)^{2}}{1-\left(\rho_{C} / \sqrt{2}\right)^{2}}}\right] \exp \left[-\frac{(2-\sqrt{2})(K / 2)}{1-\rho_{C} / \sqrt{2}}\right]
P ˉ floor = 2 1 ⎣ ⎡ 1 − 1 − ( ρ C / 2 ) 2 ( ρ C / 2 ) 2 ⎦ ⎤ exp [ − 1 − ρ C / 2 ( 2 − 2 ) ( K / 2 ) ]
Type Doppler Power Spectrum S C ( f ) ρ C = A C ( T ) / A C ( 0 ) Rectangular S 0 2 B D , ∣ f ∣ < B D sinc ( 2 B D T ) Gaussian S 0 π B D e − f 2 / B D 2 e − ( π B D T ) 2 Uniform Scattering S 0 π B D 2 − f 2 , ∣ f ∣ < B D J 0 ( 2 π B D T ) 1st Order Butterworth S 0 B D π ( f 2 + B D 2 ) e − 2 π B D T \begin{array}{|c|c|c|}
\hline \text { Type } & \text { Doppler Power Spectrum } S_{C}(f) & \rho_{C}=A_{C}(T) / A_{C}(0) \\
\hline \text { Rectangular } & \frac{S_{0}}{2 B_{D}},|f|<B_{D} & \operatorname{sinc}\left(2 B_{D} T\right) \\
\hline \text { Gaussian } & \frac{S_{0}}{\sqrt{\pi} B_{D}} e^{-f^{2} / B_{D}^{2}} & e^{-\left(\pi B_{D} T\right)^{2}} \\
\hline \text { Uniform Scattering } & \frac{S_{0}}{\pi \sqrt{B_{D}^{2}-f^{2}}},|f|<B_{D} & J_{0}\left(2 \pi B_{D} T\right) \\
\hline \text { 1st Order Butterworth } & \frac{S_{0} B_{D}}{\pi\left(f^{2}+B_{D}^{2}\right)} & e^{-2 \pi B_{D} T} \\
\hline
\end{array}
Type Rectangular Gaussian Uniform Scattering 1st Order Butterworth Doppler Power Spectrum S C ( f ) 2 B D S 0 , ∣ f ∣ < B D π B D S 0 e − f 2 / B D 2 π B D 2 − f 2 S 0 , ∣ f ∣ < B D π ( f 2 + B D 2 ) S 0 B D ρ C = A C ( T ) / A C ( 0 ) s i n c ( 2 B D T ) e − ( π B D T ) 2 J 0 ( 2 π B D T ) e − 2 π B D T
the error floor decreases with data rate R = 1 T b R = \frac{1}{T_b} R = T b 1
increasing the data rate R = 1 T b R = \frac{1}{T_b} R = T b 1
频率选择性衰减会产生ISI,即在给定的码元间隔内,接收到的码元会受到其他被多径延迟的码元的干扰。
error floor取决于ISI特性和调制格式,而ISI特性取决于信道的特性和传输符号的序列。
通过将ISI视为不相关的白高斯噪声,可得到有ISI的符号错误概率的近似值。
γ ^ s = P r N 0 B + I \hat \gamma_s=\frac{P_r}{N_0B+I}
γ ^ s = N 0 B + I P r
其中I I I
由于ISI引起的error floor可以通过仿真得到的。Chuang的结果表明,error floor对信道的均方根时延扩展比功率时延谱的形状更敏感。此外,脉冲成形可以极大地影响error floor:在升余弦脉冲中,将β \beta β
ANDREA GOLDSMITH.WIRELESS COMMUNICATIONS .2005.
(美)Andrea Goldsmith著;杨鸿文,李卫东,郭文彬等译. 无线通信. 北京:人民邮电出版社, 2007.06.
![最大似然接收机]() 有贝叶斯公式和等概率条件可以推出,要使错误率最低应满足
有贝叶斯公式和等概率条件可以推出,要使错误率最低应满足![匹配滤波器接收机]()
![调幅调相的调制与解调]()
![MPAM]()
![MPAM判决域]()
![MPAM解调]()
![MPSK]()
![MPSK_DR]()
![2PSK解调]()
![MQAM]()
![MQAM_DR]()
![差分相干解调]()
![OMPSK]()
![FM信号的调制与解调]()
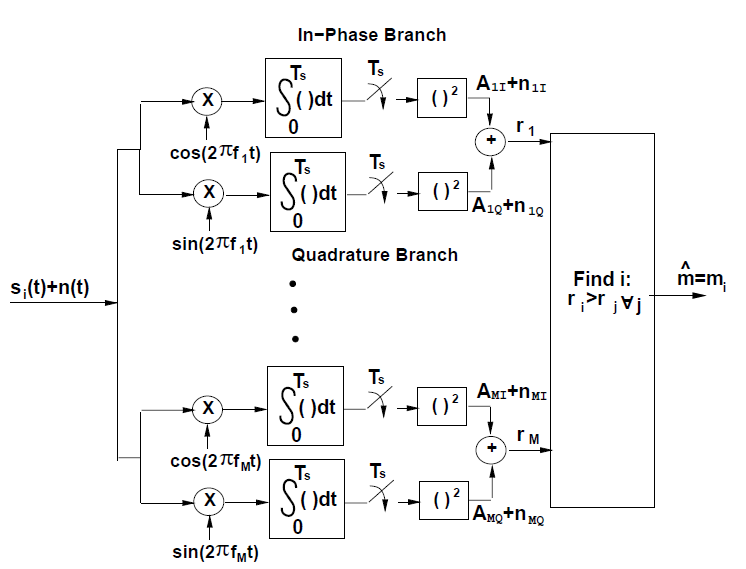
![接收机形式]()
![PLL]()
![decision-directed]()
![超前滞后门]()
![ISI]()
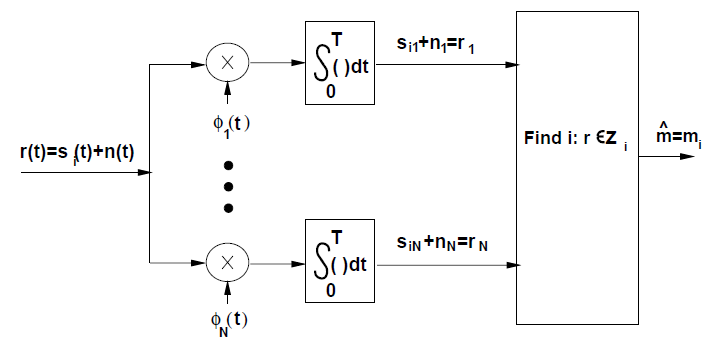 有贝叶斯公式和等概率条件可以推出,要使错误率最低应满足
有贝叶斯公式和等概率条件可以推出,要使错误率最低应满足