/ 笔记  

【无线通信学习笔记（五）】分集

Wireless Communications (Andrea Goldsmith)学习笔记。

Diversity

在“衰落信道中数字带通传输系统的性能分析”中，我们注意到瑞利衰落（多径衰落）和对数正态分布（阴影衰落）会对数字带通传输系统造成很大的影响，减轻衰落的最有力的方法就是分集-合并（diversity-combining）技术。

  • 理论依据：
    • 分：独立信号路径经由很小概率会同一时刻经历深衰落（deep fades）
    • 集：经过合并接收信号的衰落就会很小。例如选择信号最强的那根天线就是selection combining
  • 微分集（microdiversity）：减弱多径衰落（multipath）影响
  • 宏分集（macrodiversity）：减弱来自建筑、物体的阴影衰落（shadowing）
    • 做法：combining signals received by several base stations or access points

独立衰落信道（Independent Fading Paths）

  • space diversity（空间分集）：
    • 单侧阵列天线（antenna array）——多发射天线或多接收天线
    • 不增加发射功率或带宽
    • 阵列增益：相干合并可以提高信噪比，降低检测因子的要求
    • 空间分集还需要有足够大的天线间距以保证衰落幅度近似独立
      • 对于全向天线，衰落独立需要半波长
      • 对于方向性天线需要更大的天线间距
  • polarization diversity（极化分集）：
    • 两接收天线或两发射天线（水平极化和垂直极化）
    • 极化分集最有只有两个分集分支
    • 极化分集有3 dB的功率损耗
  • 方向性天线（Directional antennas）：
    • 对于方向性天线，波束对准某一角度
    • 要求有足够多天线以覆盖到所有可能的来波方向，或者一个天线恰好对准来波方向。
    • 当未对准时，信噪比将会降低
  • Frequency diversity（频率分集）：通过不同载波频率传输同一窄带信号。需要额外的发射功率
  • Time diversity（时间分集）：在不同时间传输同一信号。时间差要大于信道相干时间。

接收机分集（Receiver Diversity）

在接收机分集中，多个接收天线的独立衰落路径被结合起来，得到一个结果信号，然后通过一个标准解调器。

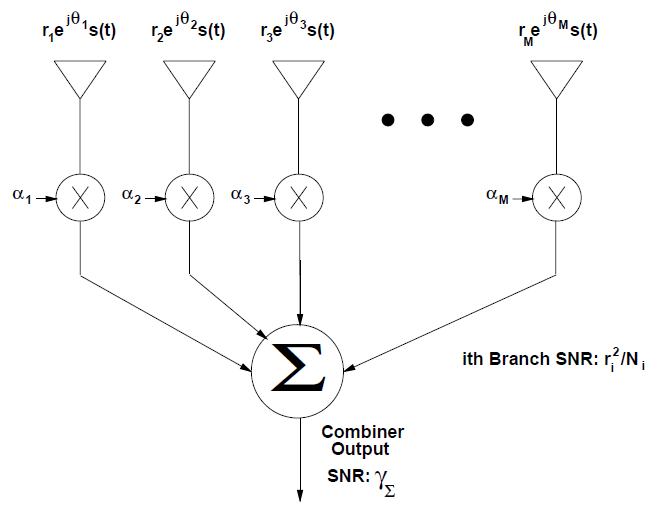
线性合并器

  • combiner的输出时不同衰落路径（分支）的加权求和，一般是线性的。

  • co-phaseing（共相位）：当合并超过一条支路是需要co-phaseing，加权时乘αi=aie−jθi\alpha_i=a_ie^{-j\theta_i}来消除相位，确保实现相干合并。一般采用先检测后合并的相干合并策略，这样可以确定合适的αi\alpha_i。

  • 分集的目的：对独立衰落信道相干合并，以减弱衰落的影响。

    αΣ=∑iairi\alpha_\Sigma=\sum_ia_ir_i

  • 阵列增益（array gain）：对多路信号的相干合并（不必在衰落条件下）。

    Ag=γˉΣγˉA_g=\frac{\bar\gamma_\Sigma}{\bar \gamma}

    对于MRC（最大比合并）：

    γΣ=MEsN0\gamma_\Sigma=\frac{ME_s}{N_0}

    相比于未合并提高了M倍。

    其实这边的概念可以用《雷达原理与系统》中的相干积累来理解，也是比较类似的。

    相干积累
    只需要相干积累前的1M\frac{1}{M}，即

    D0(M)=1MD0(1)D_0(M)=\frac 1MD_0(1)

    在相同检测条件下，相干积累增加了SNR，就可以减小对于单个脉冲串的SNR要求。对于同样作用距离，雷达可以减小发射峰值功率。

    同理对于无线通信系统来说，这里的相干合并提高了总体的信噪比，也就降低了对于每一分支SNR要求有，但是在这里我们不是为了降低发射功率，而是为了减小衰落带来的影响。

    在雷达中还有一种非相干积累，即视频积累。他在检波后进行积累就不需要相干载波，但是非相干对于无线通信来说是不可能的，因为非相干合并并没有消除相位的影响，也就没有不能消除衰落的影响。

    • 所有分集合并都有阵列增益，MRC的阵列增益最大

  • 分集增益（diversity gain）：分集带来了γΣ\gamma_\Sigma更好的分布，从而降低了平均误码率Pˉs\bar P_s和中断率PoutP_\text{out}。

    • 分集阶数（diversity order）：误码率表示为Pˉs=cγˉ−M\bar P_s=c\bar\gamma^{-M}中的cc，取决于具体调制方式。The diversity order indicates how the slope of the average probability of error as a function of average SNR changes with diversity.
    • The maximum diversity order of a system with MM antennas is MM, and when the diversity order equalsM the system is said to achieve full diversity order.

SC(选择合并)

  • 选择合并（selection combining，SC）：合并器在具有最高信噪比ri2Ni\frac{r_i^2}{N_i}的分支上输出信号。

  • 特点：

    • 如果所有分支上的噪声功率Ni=NN_i = N相同，这就相当于选择具有最高ri2+Nir^2_i + N_i的分支。
    • 只需要一个接收机，时分复用
    • 不需要co-phasing，可以应用于相干解调和差分解调

  • i.i.d Rayleigh衰落合并输出的平均信噪比：

    γˉΣ=γˉ∑i=1M1i\bar\gamma_\Sigma=\bar\gamma\sum_{i=1}^M\frac{1}{i}

    • 平均信噪比增益随MM增加而增加，但非线性。
    • 随着MM的进一步增大，阵列增益趋于0.

  • 性能分析

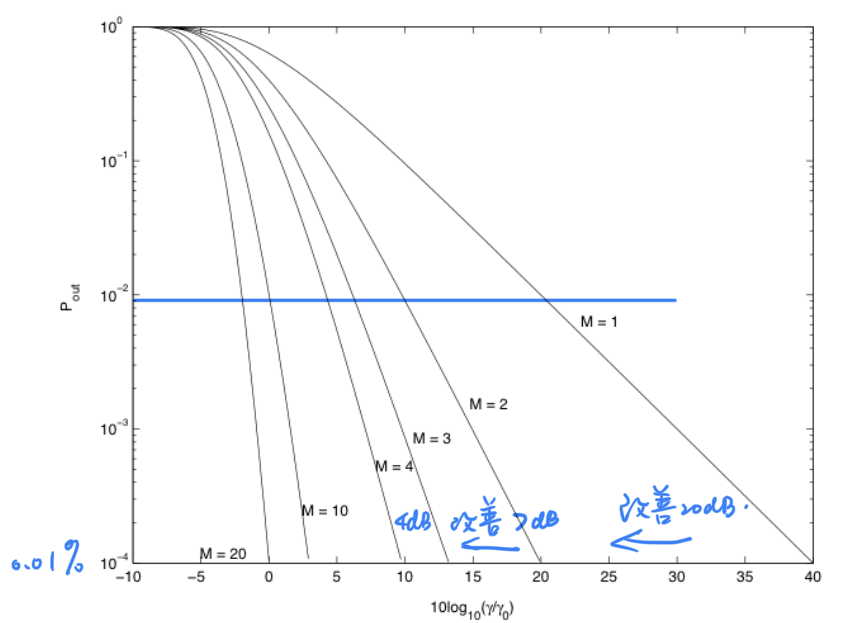
    • 给定中断率PoutP_{out}时检测因子（单支路接收信噪比）的改善(设所有支路信噪比一致)

      Pout=p(γΣ<γ0)=[1−e−γ0γˉ]MP_{out}=p(\gamma_\Sigma<\gamma_0)=\left[1-e^{-\frac{\gamma_0}{\bar \gamma}}\right]^M

      SC

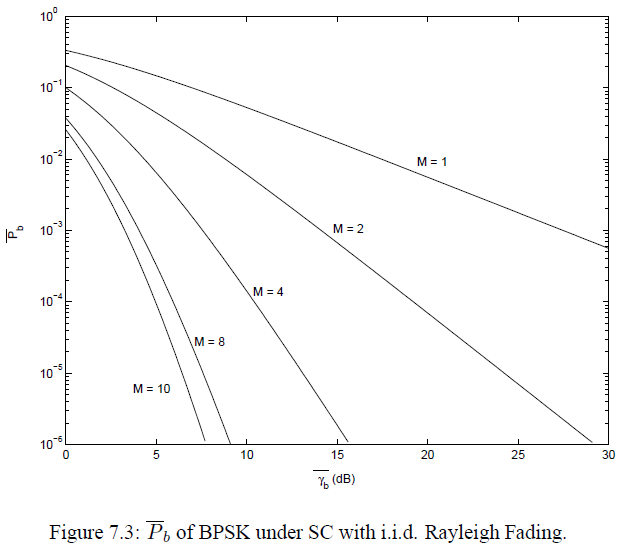
    • 给定平均误比特率Pˉb\bar P_b时的检测因子（一般无闭式解）

      pγΣ(γ)=Mγˉ[1−e−γ/γˉ]M−1e−γ/γˉ p_{\gamma_{\Sigma}}(\gamma)=\frac{M}{\bar{\gamma}}\left[1-e^{-\gamma / \bar{\gamma}}\right]^{M-1} e^{-\gamma / \bar{\gamma}}

      SC_Pb
      由于组合器的阵列增益，M≥8M\ge 8的分集系统的误比特率低于相同信噪比的AWGN信道。

Threshold Combining（门限合并）和SSC

  • 门限合并（Threshold Combining）：合并器按顺序扫描每个分支，输出信噪比高于给定阈值γT\gamma_T的第一个信号。
  • SSC（切停合并，switch and stay combining）：在只有两个分支的情况下，相当于在活动分支的信噪比低于γT\gamma_T时切换到另一个分支。性能介于无分集和SC之间。
  • 性能分析：
    • 在任意衰落分布下，对于最佳门限的SSC和SC有相同的中断率。
    • 采用SSC的相干解调，平均误比特率一般没有闭式解

MRC（最大比合并）

  • 最大比合并（Maximal Ratio Combining，MRC）：合并器输出各分支信号的加权求和。

  • 合并输出信噪比：

    max⁡aiγΣ=r2Ntot=1N0(∑i=1Mairi)2∑i=1Mai2\max_{a_i} \gamma_{\Sigma}=\frac{r^{2}}{N_{t o t}}=\frac{1}{N_{0}} \frac{\left(\sum_{i=1}^{M} a_{i} r_{i}\right)^{2}}{\sum_{i=1}^{M} a_{i}^{2}}

    最佳加权值为ai2=ri2N0a_i^2=\frac{r_i^2}{N_0}，合并输出信噪比为

    rΣ=∑i=1Mri2N0=∑i=1Mγir_{\Sigma}=\sum_{i=1}^M\frac{r^2_i}{N_0}=\sum_{i=1}^M\gamma_i

    可见，合并输出的平均信噪比随分集分支MM增加而线性增加。

  • 性能分析

    • 中断率：

    • 平均误码率可由合并输出信噪比的分布求得：

  • MRC的性能远好于SC

  • 用MGF求MRC分集的平均误码率

    • 平均误码率通式：

      Pˉs=∫0∞c1exp⁡[−c2γ]pγΣ(γ)dγ\bar{P}_{s}=\int_{0}^{\infty} c_{1} \exp \left[-c_{2} \gamma\right] p_{\gamma_{\Sigma}}(\gamma) d \gamma

      用MGF表示

      Pˉs=c1∫AB∏i=1M∫0∞exp⁡[−c2(x)γi]pγi(γi)dγi=c1∫AB∏i=1MMγi(−c2(x))dx\bar{P}_{s}=c_{1} \int_{A}^{B} \prod_{i=1}^{M} \int_{0}^{\infty} \exp \left[-c_{2}(x) \gamma_{i}\right] p_{\gamma_{i}}\left(\gamma_{i}\right) d \gamma_{i}=c_{1} \int_{A}^{B} \prod_{i=1}^{M} M_{\gamma_{i}}\left(-c_{2}(x)\right) d x

      适用于任意分集分支和任意支路衰落分布

    • 具体调制与衰落分布的平均误码率这里不抄了

  • γi\gamma_i分布相同，高信噪比时的平均误码率

    Pˉs≈αM(βMγˉ2)−M\bar P_s\approx\alpha_M\left(\frac{\beta_M\bar \gamma}{2}\right)^{-M}

    分集阶数为M，为满分集阶数

EGC（等增益合并）

  • 等增益合并（Equal-Gain Combining，EGC）：以相同权重αi=e−jθi\alpha_i=e^{-j\theta_i}对所有分支加权求和。

    基本上就是相干解调的意思了。

  • 合并输出信噪比

    γΣ=1N0M(∑i=1Mri)2\gamma_{\Sigma}=\frac{1}{N_{0} M}\left(\sum_{i=1}^{M} r_{i}\right)^{2}

  • 性能分析：

    • 中断率：

      Pout (γ0)=1−e−2γ0γˉ−πγ0γˉe−γ0γˉ(1−2Q(2γ0γˉ))P_{\text {out }}\left(\gamma_{0}\right)=1-e^{-2 {\frac{\gamma_0}{\bar\gamma}}}-\sqrt{\pi \frac{\gamma_0}{\bar\gamma}} e^{-\frac{\gamma_0}{\bar\gamma}}\left(1-2 Q\left(\sqrt{2 \frac{\gamma_0}{\bar\gamma}}\right)\right)

    • 平均误码率可由输出信噪比的分布求得

      pγΣ(γ)=1γˉe−2γ/γˉ+πe−γ/γˉ(14γγˉ−1γˉγγˉ)(1−2Q(2γ/γˉ))p_{\gamma_{\Sigma}}(\gamma)=\frac{1}{\bar{\gamma}} e^{-2 \gamma / \bar{\gamma}}+\sqrt{\pi} e^{-\gamma / \bar{\gamma}}\left(\frac{1}{\sqrt{4 \gamma \bar{\gamma}}}-\frac{1}{\bar{\gamma}} \sqrt{\frac{\gamma}{\bar{\gamma}}}\right)(1-2 Q(\sqrt{2 \gamma / \bar{\gamma}}))

  • EGC的性能非常接近MRC，功率损耗不超过1 dB，但是复杂度更低。

  • 用MGF求EGC分集的平均误码率

    • MGFs are less useful in the analysis of EGC and SC than in MRC.
    • working with the MGF of γΣ\gamma_\Sigma can sometimes lead to simpler results than working directly with its pdf. 比如将ss变为j2πfj2\pi f就将MGF变为特征函数，可以求得EGC分集MPSK的误码率的精确式。

发射机分集（Transmitter Diversity）

发射机分集一般被用在有充足的空间、功率和处理能力的地方。假设CSIR（Receiver CSI）讨论接收机是否知道CSI。

CSIR和CSIT

  • CSIT：发射机已知第ii根天线上的路径增益riejθir_ie^{j\theta_i}

  • 最大化接收信噪比

    γΣ=EsN0∑i=1Mri2=∑i=1Mγi\gamma_{\Sigma}=\frac{E_{s}}{N_{0}} \sum_{i=1}^{M} r_{i}^{2}=\sum_{i=1}^{M} \gamma_{i}

    此时的加权值

    ai=ri∑i=1Mri2a_i=\frac{r_i}{\sqrt{\sum_{i=1}^Mr_i^2}}

    当CSIT，发射机分集与MRC分集类似。接受信噪比为各支路信噪比之和

  • γi\gamma_i分布相同，高信噪比时的平均误码率

    Pˉs≈αM(βMγˉ2)−M\bar P_s\approx\alpha_M\left(\frac{\beta_M\bar \gamma}{2}\right)^{-M}

    分集阶数为M，为满分集阶数

  • 发射机分集的问题：发射机获取信道相位和幅度信息

    • 导频（pilot technique）
    • 利用时分（time-division）的互易性（reciprocal）

仅CSIR——The Alamouti Scheme

该方案在两个符号周期内工作，假定信道增益在这段时间内是不变的。在第一个码元间隔，两个不同的码元s1s_1和s2s_2分别从天线1和2同时传输，每个码元的能量为Es2\frac{E_s}{2}。在下一个码元间隔，符号s2∗s^∗_2从天线1发射，符号s1∗s^∗_1从天线2发射，每个码元能量为$ \frac{E_s}{2}$。

接收信号

y=[h1h2h2∗−h1∗][s1s2]+[n1n2∗]=HAs+n\mathbf{y}=\left[\begin{array}{cc} h_{1} & h_{2} \\ h_{2}^{*} & -h_{1}^{*} \end{array}\right]\left[\begin{array}{l} s_{1} \\ s_{2} \end{array}\right]+\left[\begin{array}{c} n_{1} \\ n_{2}^{*} \end{array}\right]=\mathbf{H}_{A} \mathbf{s}+\mathbf{n}

接收信噪比

γi=(∣h12∣+∣h22∣)Es2N0\gamma_{i}=\frac{\left(\left|h_{1}^{2}\right|+\left|h_{2}^{2}\right|\right) E_{s}}{2 N_{0}}

分集阶数为2，但阵列增益只有1.

这章内容和《雷达原理与系统》里面的雷达信号检测部分有异曲同工之妙，但是雷达往往发射重频信号，可以采用积累的方法来降低降低因子。而在无线通信中，我们不太可能反反复复发射一样的信号，所以就采用分集-合并的方式来降低对于检测因子的要求。但是有一些思路是一致的。

参考文献

  1. ANDREA GOLDSMITH.WIRELESS COMMUNICATIONS.2005.
  2. （美）Andrea Goldsmith著；杨鸿文，李卫东，郭文彬等译. 无线通信. 北京：人民邮电出版社, 2007.06.

本文标题:【无线通信学习笔记（五）】分集

文章作者:Levitate_

发布时间:2021年05月06日 - 20:00:00

原始链接:https://levitate-qian.github.io/2021/05/07/Wireless-Communications-Ch-7/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。