如果没有意外的话,我应该有学上了!
所以我又准备开始更新博客了。
这个深度学习专项是杨神推荐的,链接为https://www.coursera.org/specializations/deep-learning(可能需要挂梯子)。吴恩达老师的英语非常通俗易懂啊,基本上开着英文字幕就能听,不需要中文字幕😜。
这个专项课程一共五门,包括
- Neural Networks and Deep Learning(神经网络与深度学习)
- Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization(改进深度神经网络:超参数、正则化和优化)
- Structuring Machine Learning Projects(构建机器学习项目)
- Convolution Neural Networks(卷积神经网络)
- Sequence Model(序列模型)
目前我还在学第四门,我准备把每门课的内容在博客上梳理一下。
——3月25日
第四门学完啦,第五门第一周也学完啦。又来更新了!
——4月5日
Neural Networks and Deep Learning 学习笔记
第一门课的主体框架
- Week 1: Introduction
- Week 2: Programming
- Week 3: Singal hidden layer NN
- Week 4: Deep NN
Week 1
Welcome to the Deep learning Specilization主要就是五门课程的总体介绍,这里就不放了。
Introduction to Deep Learning
这个section主要介绍了神经网络和深度学习最基础的内容,并分析了为何深度学习会在当今take-off。
1. Neural Network
![neural]()
2. Supervised learning with neural network
- 监督学习:输入为x,输出为y。(即有标签)
- 分不同类型神经网络的应用范围
- 标准神经网络(Standard NN):房地产,网上广告
- 卷积神经网络(Convolution NN, CNN):图像标语
- 循环神经网络(Recurrent NN,RNN):语音识别,翻译
- Hybrid:自动驾驶
- 监督学习的对象主要有两种
- Structured Data:类似于数据表
- Unstructured Data:如音频、图像、文本
3. Why DL take-off? (Why now?)
Scale drives deep learning progress. (规模驱动深度学习的发展)
- Data(近几年来数据收集量越来越大)
- Computation
- Algorithm
重要的循环
![循环]()
Week 2
Logistic Regression as a NN
在这个section中,讲述的是Logistic回归的相关内容,主要包括Logistic回归的正向(cost function)和反向传播(梯度下降最小化cost function),并对Python、numpy、jupyter notebook的使用做了讲解。
1. Binary Classification
- 二元分类(Binary Classification): x→y
- 例如处理一幅64×64像素猫的图像时,先将其分成RGB三个通道,再将其unroll成一个列向量,其维数为64×64×3=12288。此时该图像即Binary Classification中的输入x。标记(label)用于分类是否为猫,即为y。
- 符号说明:
- One training example: (x,y), x∈Rnx,y∈{0,1}
- m training example: {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))}
- 其中m可以取为mtrain,mtest分别表示训练样本的个数和测试样本的数量
- 训练集:X=⎣⎢⎢⎡∣x(1)∣∣x(2)∣⋮⋯⋮∣x(m)∣⎦⎥⎥⎤,X∈Rnx×m,是一个(nx,m)维的矩阵。
- 标签:Y=[y(1),y(2),⋯,y(m)],Y∈R1×m,是一个(1,m)维的矩阵。
2. Logistic Regression & cost function
-
单个样本Logistic Regression的主要流程
Given x∈Rnx, want y^=P(y=1∣x),0≤y^≤1(即希望y^是y=1的一个良好估计)
Parameter: w∈Rnx,b∈R
Output: y^=wT+b (linear regression)
y^=σ[wT+b](logistic regression,其中σ[∙]是sigmoid function)
此外也可以表示为y^=ΘTx(x0=1,x∈Rnx+1)
其中ΘT=⎣⎢⎢⎢⎡θ0θ1⋮θnx⎦⎥⎥⎥⎤→b⎱→w⎰
-
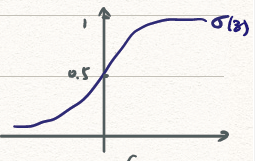
sigmoid function
![sigmoid_function]()
σ(z)=1−e−z1
其中,当z→−∞时,1+∞1=0;当z→∞时,1+01=1
-
对于m个样本的Logistic regression
y^=σ(wTx+b), where σ(z(i))=1+e−z(i)1
Given {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))}, want y^(i)=y(i)
其中,上标(i)表示第i个training example。
-
Loss Function(损失函数,针对单个样本来说)
L(y^,y)=−(ylogy^+(1−y)log(1−y^))
- 当y=1时,希望y^越大越好
- 当y=0时,希望y^越小越好
-
Cost function(代价函数,针对全体样本来说,是cost of parameter)
J(w,b)==m1i=1∑mL(y^(i),y(i))−m1i=1∑m(y(i)logy^(i)+(1−y(i))log(1−y^(i)))
3. Gradient Descent
-
Gradient Descent基础
![gradient_descent]()
- 梯度下降实际上就是沿着w,b梯度(简记作∂w∂J(w,b)=dw,∂b∂J(w,b)=db)下降方向,即
Repeat{
w:=w−αdw
b:=b−αdb
}
- 其中α是learning rate。
- 计算∂w∂J(w,b)=dw,∂b∂J(w,b)=db的方式是利用计算图(Computation Graph),其实就是多元微分的内容,即“连线相乘,分线相加,一元全导,多元偏导”。但吴恩达也说在实际应用中,我们只需要考虑正向传播,而不需要考虑反向传播,框架可以自己处理反向传播。
-
Logistic Regression Gradient descent on one example
LogisticL Regression的步骤主要包括以下三步:
- z=wTx+b
- y^=a=σ(z)
- L(a,y)=−(yloga+(1−y)log(1−a))
![Logistic Regression Gradient descent]()
计算得
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂w1∂L=∂w2∂L=∂b∂L=∂a∂L⋅za⋅∂w1∂z(−ay+1−a1−y)⋅a(1−a)⋅x1=(a−y)x1(a−y)x2a−y
⇒⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧w1:=w2:=b:=w1−α∂w1∂Lw2−α∂w2∂Lb−α∂b∂L
其中σ(z)=1+e−z1的导数推导如下
(1+e−z1)′=(1+e−z)−2e−z=(1+e−z)2e−z=1+e−ze−z+1−1⋅1+e−z1=(1−1+e−z1)⋅1+e−z1=(1−σ(z))σ(z)
-
Gradient descent on m example
-
Cost function
J(ω,b)=m1i=1∑mL(ai,y)a(i)=y^(i)=σ(z)=σ(ω⊤x(i)+b)∂w1∂J(w,b)=m1i=1∑m∂w1∂L(a(i),y)
-
算法
![Gradient_descent_on_m_example]()
可以注意到在上述算法中存在两个显式的for-loop,这对于加快运算是非常不利的。
-
解决显式for-loop的方法:Vectorization(向量化)
Python and Vectorization
1. Vectorization
Whenever possible, avoid explicit for-loops.
-
举例
-
【Example·01】z=wTx+b,其中w是一个列向量,x也是一个列向量。
Vectorization:z = np.dot(w, x) + b
-
【Example·02】u=Av
non-Vectorization: ui=∑jAijvj(存在两重for-loop)
Vectorization: u = np.dot(A, v)
-
【Example·03】
v=⎣⎢⎢⎢⎡v1v2⋮vn⎦⎥⎥⎥⎤⇒u=⎣⎢⎢⎢⎡ev1ev2⋮evn⎦⎥⎥⎥⎤
Vectorization: u = np.exp(v)
-
另外还可以使用np.log(v), np.abs(v), np.maximum(v, 0), v ** 2, 1 / v。
-
针对logistic regression derivatives的改进(改进第二个for-loop)
J=0, dw=np.zeros([nx,1]), db=0
For i=0 to m
z(i)=wTx(i)+b
ai=σ(z(i))
J+=−[y(i)loga(i)+(1−y(i))log(1−a(i))]
dz(i)=a(i)−y(i)
dw+=x(i)dz(i)
db+=dz(i)
J/=m; dw/=m; db/=m;
注意其中加粗部分即为利用vectorization的部分。
2. Vectorizing Logistic Regression
-
各参数的矩阵表示:
X=Z===dZ==db=dw=⎣⎢⎢⎡∣x(1)∣∣x(2)∣⋮⋯⋮∣x(m)∣⎦⎥⎥⎤,X∈Rnx×m[z(1),z(2),⋯,z(m)]1×mwTX+[b,b,⋯,b]1×m=[wTx(1)+b,wTx(2)+b,⋯,wTx(m)+b]1×mnp.dot(w.T,X)+b[dz(1),dz(2),⋯,dz(m)]1×m=[a(1)−z(1),a(2)−z(2),⋯,a(m)−z(m)]1×mA−Ym1i=1∑mdz(i)=np.sum(dZ)m1XdZT=⎣⎢⎢⎡∣x(1)∣∣x(2)∣⋮⋯⋮∣x(m)∣⎦⎥⎥⎤⎣⎢⎡dz(1)⋮dz(m)⎦⎥⎤
-
算法:
Z==A=dZ=dw=db=w=b=wTX+bnp.dot(w.T,X)+bσ(Z)A−Ym1XdZTm1np.sum(dZ)w−αdwb−αdb
即使对参数进行了vectorization,for-loop仍然是需要的。
3. Broadcasting in Python
![Broadcasting]()
4. Notes & Tips on Python/numpy
![note]()
Week 3
Shallow NN
NN short for Neural Network.
本section主要介绍单层的神经网络(Shallow NN),介绍了Shallow NN的正向传播(forward prop)和反向传播(Back prop)过程,并讲解了常见的激活函数(Activation Function)和随机初始化(Random Initialization)的相关内容。
1. NN overview
-
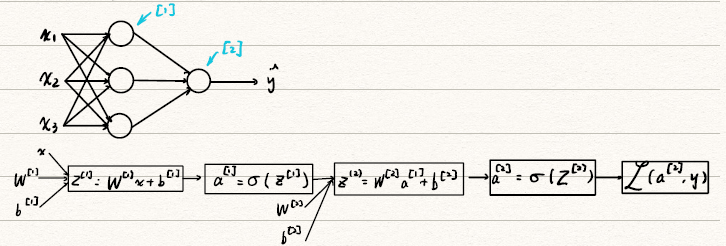
NN的计算
![Shallow_NN_overview]()
-
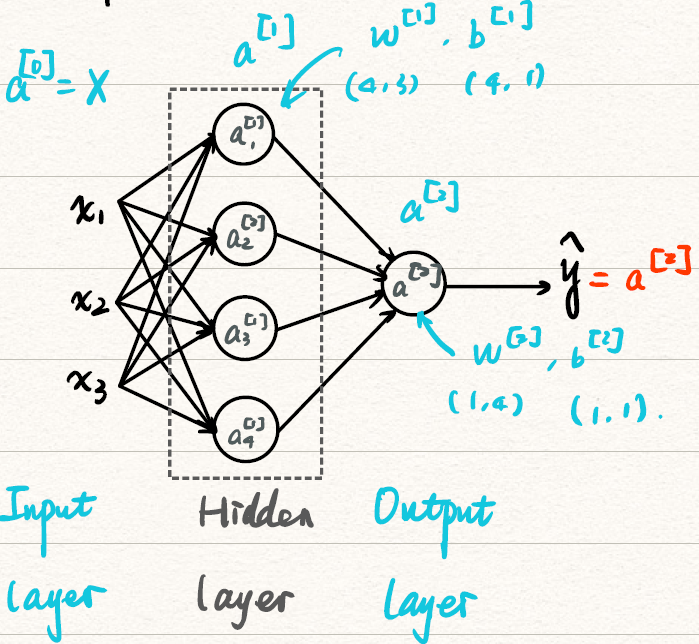
NN的表示
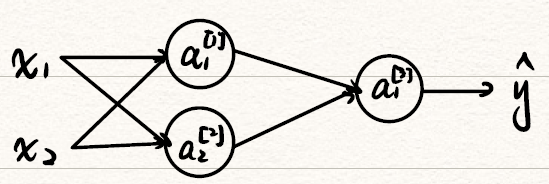
![NN_representation]()
如图所示是一个2层的神经网络,因为输入层不计入。
- 用上标[i]表示第i层
- 每个矩阵的维数见图中。
- 注意到我们把输入层x也表示为a[0]
2. Computing a NN’s Output & Vectorizing
-
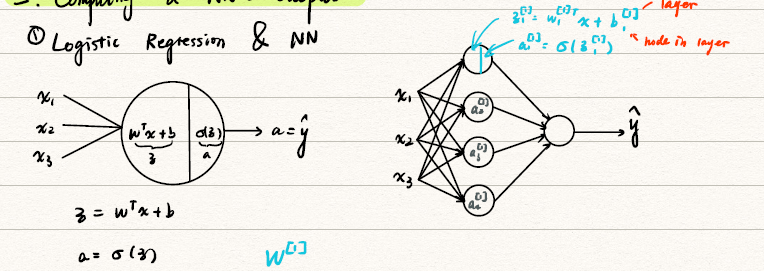
取其中一个unit计算结果,左图显示了只有一个hidden layer,且只有一个unit的情况。
![Logistic_nn]()
如左图所示,在神经元中的计算主要包括线性的z=wTx+b和非线性激活函数a=σ(z)两部分,最后输出的预测结果y^=a。从右图可以看到hidden layer的每一个都是这unit样两步。
-
矩阵表示
σ(z[1])==σ⎝⎜⎜⎜⎛⎣⎢⎢⎢⎡−−−−w1[1]Tw2[1]Tw3[1]Tw4[1]T−−−−⎦⎥⎥⎥⎤4×3⎣⎡x1x2x3⎦⎤3×1+⎣⎢⎢⎢⎡b1[1]b2[1]b3[1]b4[1]⎦⎥⎥⎥⎤4×1⎠⎟⎟⎟⎞σ⎝⎜⎜⎜⎛⎣⎢⎢⎢⎡w1[1]Tx+b1[1]w2[1]Tx+b2[1]w3[1]Tx+b3[1]w4[1]Tx+b4[1]⎦⎥⎥⎥⎤4×1⎠⎟⎟⎟⎞=σ⎝⎜⎜⎜⎛⎣⎢⎢⎢⎡z1[1]z2[1]z3[1]z4[1]⎦⎥⎥⎥⎤⎠⎟⎟⎟⎞
-
对于1个样本的算法:(右下角标注的是维数)
Given input x:
z4×1[1]=W4×3[1]a3×1[0]+b4×1[1]a4×1[1]=σ(z4×1[1])}z1×1[2]=W1×4[2]a4×1[1]+b1×1[2]a1×1[2]=σ(z1×1[2])}layer 1layer 2
-
Vectorizing across multiple examples(多个样本进行Vectorization)
-
对于a[2](i)
- [2]表示Layer 2(第二层)
- (i)表示第i个training example
-
对于m个样本的算法:
for i=0 to m:
z[1](i)=a[1](i)=z[2](i)=a[2](i)=W[1]x(i)+b[1]σ(z[1](i))W[2]a[1](i)+b[2]σ(z[2](i))
-
Vectorization
Z[1]=A[1]=Z[2]=A[2]=W[1]X+b[1]σ(Z[1])W[2]A[1]+b[2]σ(Z[2])
其中,X=⎣⎢⎢⎡∣x(1)∣∣x(2)∣⋮⋯⋮∣x(m)∣⎦⎥⎥⎤nx×m, Z[1]=⎣⎢⎢⎡∣z[1](1)∣∣z[1](2)∣⋮⋯⋮∣z[1](m)∣⎦⎥⎥⎤, A[1]=⎣⎢⎢⎡∣a[1](1)∣∣a[1](2)∣⋮⋯⋮∣a[1](m)∣⎦⎥⎥⎤,其水平方向是training examples的数量,垂直方向是hidden unit的数量。
-
Explanation for vectorized Implementation
![Explanation_for_vectorized_Implementation]()
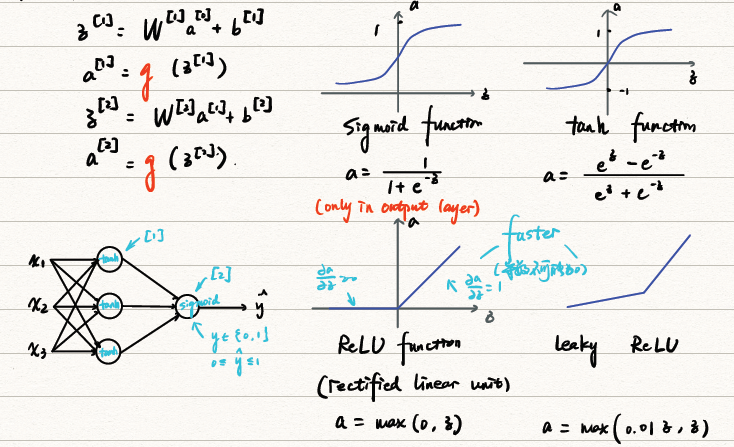
3. Activation Function
-
常用的activation function
![activation_function]()
-
Why non-linear activation function?
如果使用线性激活函数,则在重复进行线性计算。根据线性运算的齐次性和叠加性,易知该情况和无hidden layer的情况没有区别。即无法构建Deeper NN。
-
Derivatives of activation function
-
sigmoid function
g(z)=1+e−z1g′(z)=g(z)(1−g(z))
- z→∞(10): g′(z)=0
- z→−∞(10): g′(z)=0
- z→0: g′(z)=41
-
tanh function
g(z)=ez+e−zez−z−zg′(z)=1−tanh2(z)
- z→∞(10): g′(z)=0
- z→−∞(10): g′(z)=0
- z→0: g′(z)=1
-
ReLU & leaky ReLU
-
ReLU:
g(z)=max(0,z)g′(z)={0,1, if z<0 if z>0
-
leaky ReLU:
g(z)=max(0.01z,z)g′(z)={0.01,1, if z<0 if z>0
4. Gradient Descent & Back propagation
-
Gradient Descent for NN
-
参数: wn[1]×n[0][1],bn[1]×1[1],wn[2]×n[1][2],wn[2]×1[2],nx=n[0],n[1],n[2]=1
-
Cost function: J(w[1],b[1],w[2],w[2])=m1∑i=1mL(y^,y)
-
Gradient descent:
Repeat{
Compute predictions (y^(i),i=1,2,⋯,m)
dw[1]=∂w[1]∂J,db[1]=∂b[1]∂J,⋯
w[1]:=w[1]−αdw[1]
b[1]:=b[1]−αdb[1]
同理计算w[2],b[2]}
-
Formula for computing derivatives
| Forward propagation |
Back propagation |
| Z[1]=W[1]X+b[1]A[1]=g[1](Z[1])Z[2]=W[2]A[1]+b[2]A[2]=g[2](Z[2]) |
dZ[2]=A[2]−YdW[2]=m1dZ[2]A[1]Tdb[2]=m1np.sum(dZ[2],axis=1,keepdims=True)dZ[1]=W[2]TdZ[2]∗g[1]′(z[1])dW[1]=m1dZ[1]XTdb[1]=m1np.sum(dZ[1],axis=1,keepdims=True) |
- 其中
axis = 1表示按行加
- W[2]TdZ[2]和g[1]′都是n[1]×m维的。
*表示element wise
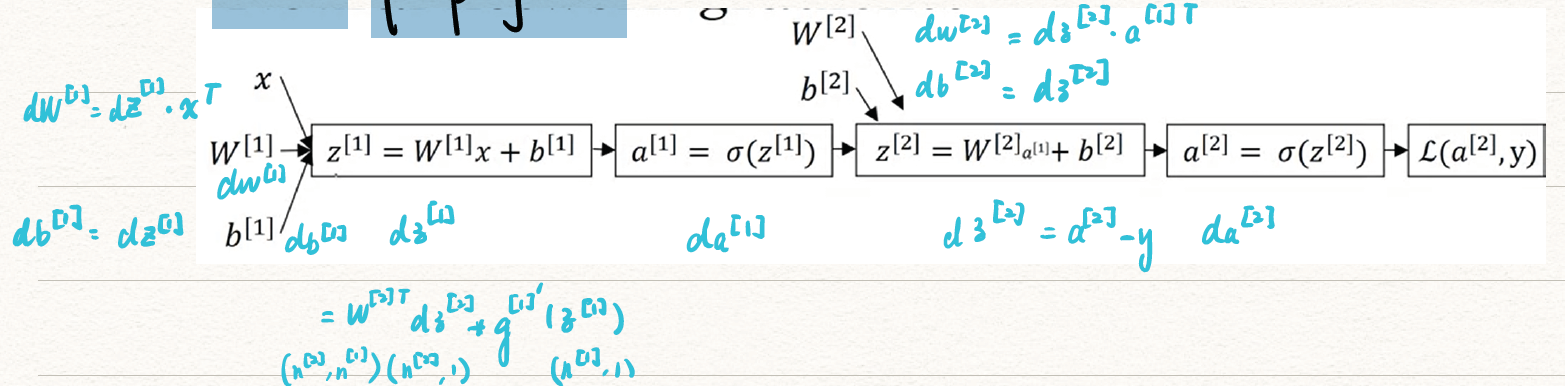
-
Back propagation
![back_prop]()
对于m个examples,
dZ[2]=A[2]−YdW[2]=m1dZ[2]A[1]Tdb[2]=m1np.sum(dZ[2],axis=1,keepdims=True)dZ[1]=W[2]TdZ[2]∗g[1]′(z[1])dW[1]=m1dZ[1]XTdb[1]=m1np.sum(dZ[1],axis=1,keepdims=True)
5. Random Initialization
![random_initialization]()
-
为什么不能将初始的weight初始化为0?
若W[1]=[0000],则两个unit算的结果是相同的,每一个hidden layer的unit多少就没有意义了。同时对其求gradient,dW[1]=[uuvv]
-
恰当的初始化方式为:
W[1]=np.random.randn((2,2))∗0.01(这步*0.01主要是为了获得一个比较小的靠近0的初始值,这是考虑到sigmoid function只在0附近的取值存在一定的线性,而过大趋于1,过小趋于0)
b[1]=np.zeros((2,1))(由于对于weight的取值已经随机了,bias是否随机不再重要)
对于W[2],b[2]的取值和上述类似。
Week 4
Deep NN
1. DNN Overview
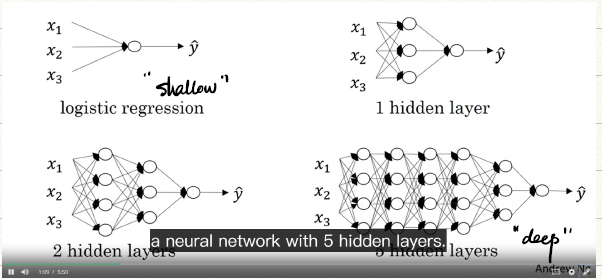
-
在week 3主要介绍的是Shallow NN,随着hidden layer越来越多,也就越来越deeper了。
![shallow-to-deep]()
-
notations
![dnn_noatations]()
根据上图介绍notations:
- number of layer(#layer): L=4
- number of units of layer l: n[l]
- activations of layer l: a[l]=g[l](z[l])
- weight for z[l]: w[l]
- bias for z[l]: b[l]
2. Forward Propagation in a Deep Network
-
和Shallow NN类似,计算forward propagation的过程,如下表左侧。若对其进行vectorized,则变为右侧形式。
| Elements |
Vectorization |
| z[1]=w[1]x+b[1]a[1]=g[1](z[1])z[2]=w[2]a[1]+b[2]a[2]=g[2](z[2])⋯z[4]=w[4]a[3]+b[4]a[4]=g[4](z[4]) |
Z[1]=W[1]X+b[1]A[1]=g[1](Z[1])Z[2]=W[2]A[1]+b[2]A[2]=g[2](Z[2])⋯Z[4]=W[4]A[3]+b[4]A[4]=g[4](Z[4]) |
更一般的可以写作
Z[l]=W[l]A[l−1]+b[l]A[l]=g[l](Z[l])
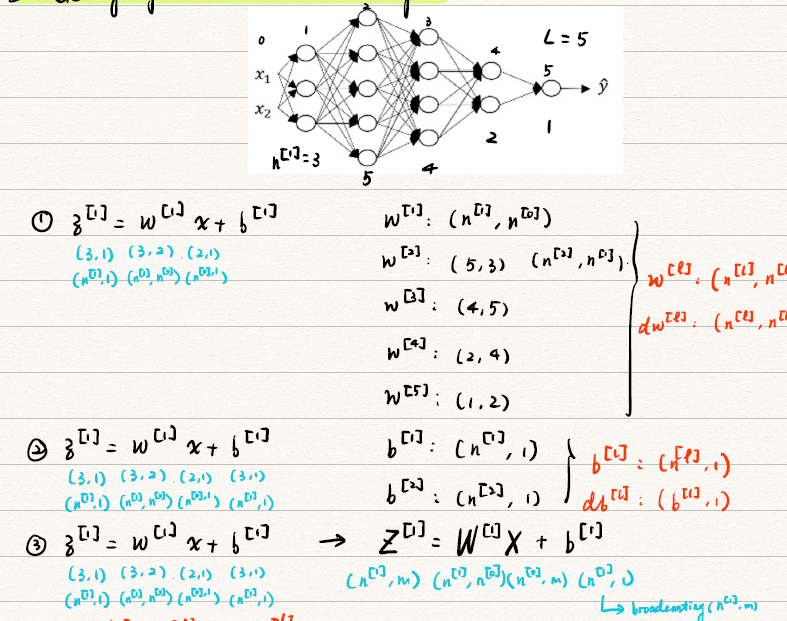
-
在处理DNN的forward propagation时需要注意矩阵的维数是否正确。下面是一个例子
![dnn_demension]()
下面归纳单个样本Deep NN中出现的各个参数的维度:
- w[l],dw[l]:(n[l],n[n−1])
- b[l],db[l]:(n[l],1)
- z[l],a[l]:(n[l],1)
针对m个样本来说:
- Z[l],A[l]:(n[l],m)(特别地,当l=0时,A[0]=X:(n[0],m))
- dZ[l],dA[l]:(n[l],m)
-
Why deep representation?为何“深度”的NN表现更好?
- 在early layer,网络主要实现一些简单功能,例如边缘的检测;在对其进行组合后,即到了later layer时,网络将实现一些复杂的功能,例如分类器。
- 类似于数字电路理论中的与、或、非门和与非门,层数越多可以减少每个隐层的units的数量
3. Backward Propagation
-
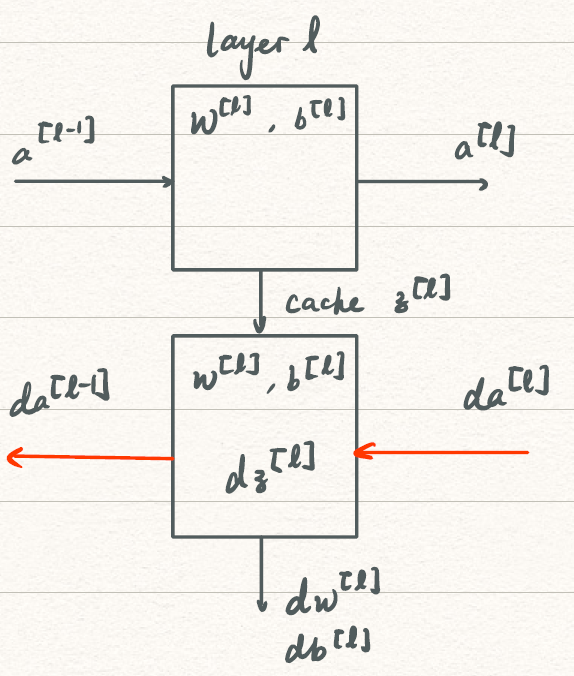
Building blocks of DNN
blocks可以表明在前向传播的过程中需要对应传递那些参数用于反向传播。
-
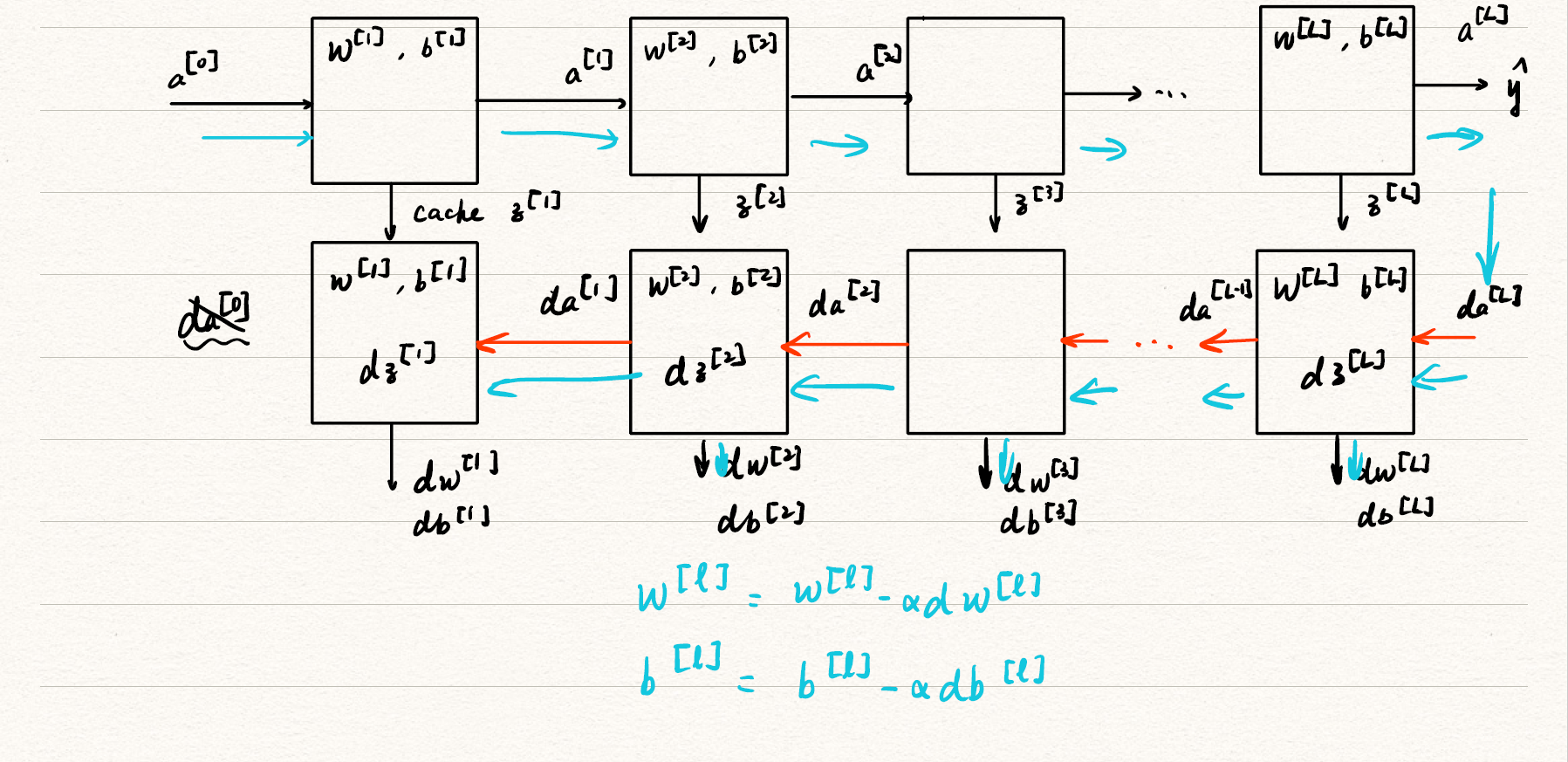
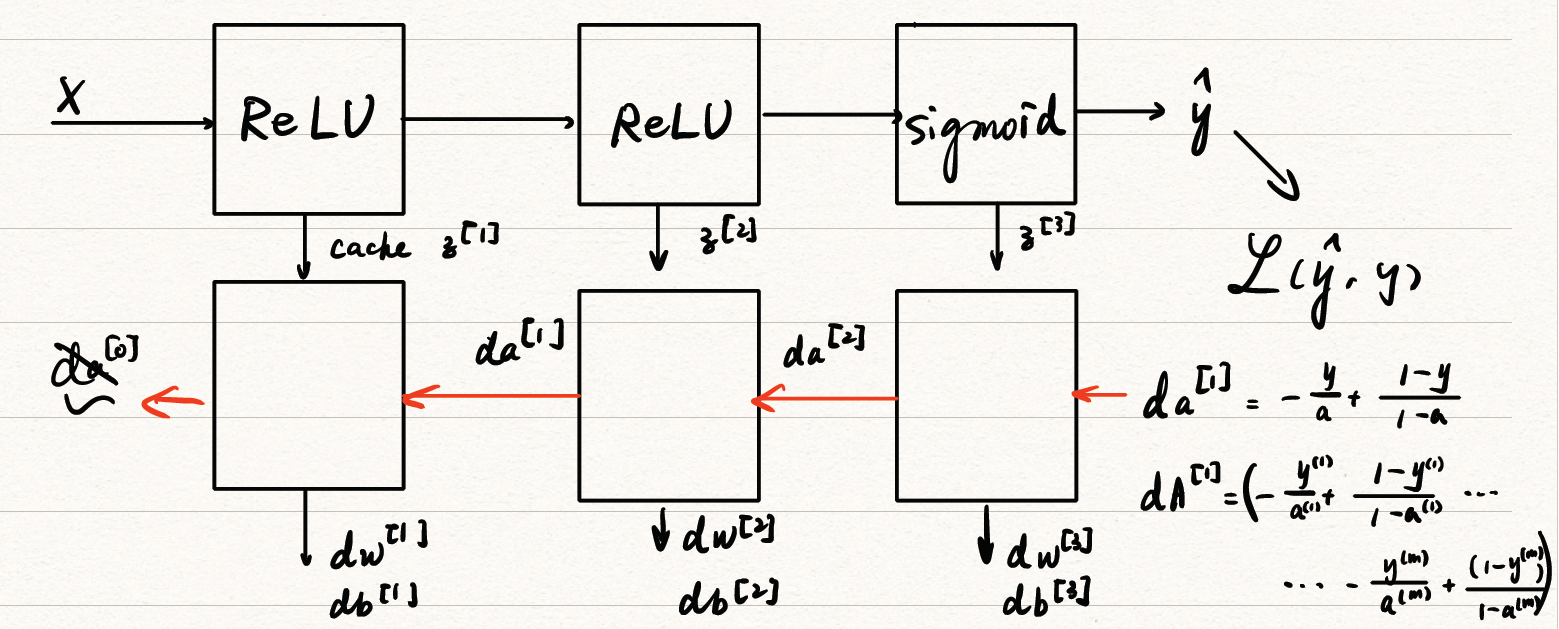
Forward & Backward Propagation
上面构建了block用于分析前向传播的过程中需要对应传递那些参数用于反向传播,下面利用传递的参数构建DNN的反向传播公式。DNN的正、反向传播公式如下:
-
FORWARD
- 输入:a[l−1]
- 输出:a[l],cache(z[l])
- Z[l]=W[l]A[l−1]+b[l]
A[l]=g[l](Z[l])
-
BACKWARD
-
输入:da[l]和先前cache的z[l]
-
输出da[l−1],dw[l],db[l]
| one example |
m examples |
| dz[l]=dw[l]=db[l]=da[l−1]=dzl=da[l]∗g[l]′(z[l])dz[l]⋅a[l−1]Tdz[l]w[l]T⋅dz[l]w[l+1]T⋅dz[l+a]∗g[l]′(z[l]) |
dZ[l]=dW[l]=db[l]=dA[l−1]=dA[l]∗g[l]′(z[l])m1dZ[l]A[l−1]Tm1np.sum(dZ[l],axis=1,keepdims=True)W[l]T⋅dZ[l] |
-
其结构如图
![dnn_prop]()
4. Parameters & Hyperparameters
Hyperparameters其实是Course 2主要研究的问题,在这里只是提了一下什么是超参数(Hyperparameters)。
- 参数:W[1],b[1],W[2],b[2],⋯
- 超参数:(吴恩达用
#表示number of …)
- learning rate α
- #iterations
- #hidden layer L
- #hidden units n[1],n[2],⋯
- choice of activation function
- 包括Course 2中将涉及的momentum, mini-batch, regulations, …
- 参数根据超参数的改变是会有很大的变化的,即Hyperparameters control parameters.
Applied deep learning is a very empirical process.
5. Deep learning and brain
![brain]()
- 这个笔记主要是我看coursera课程是笔记的整理,所以文章里面肯定是很多疏漏,也存在很多错误的,欢迎在评论区批评指正。(求轻喷
- 由于整理打公式还是非常麻烦的,也很容易出错,所以会有一些写的不太规范的地方,大家见谅。
- 不知道为什么好好的表格到网页框线就没了,大家将就看吧。/(ㄒoㄒ)/~~

![sigmoid_function]()
![gradient_descent]()
![Logistic Regression Gradient descent]()
![Gradient_descent_on_m_example]()


![Shallow_NN_overview]()
![NN_representation]()
![Logistic_nn]()
![Explanation_for_vectorized_Implementation]()
![activation_function]()
![back_prop]()
![shallow-to-deep]()
![dnn_noatations]()
![dnn_demension]()
![dnn_single_block]()
![dnn_blocks]()
![dnn_prop]()