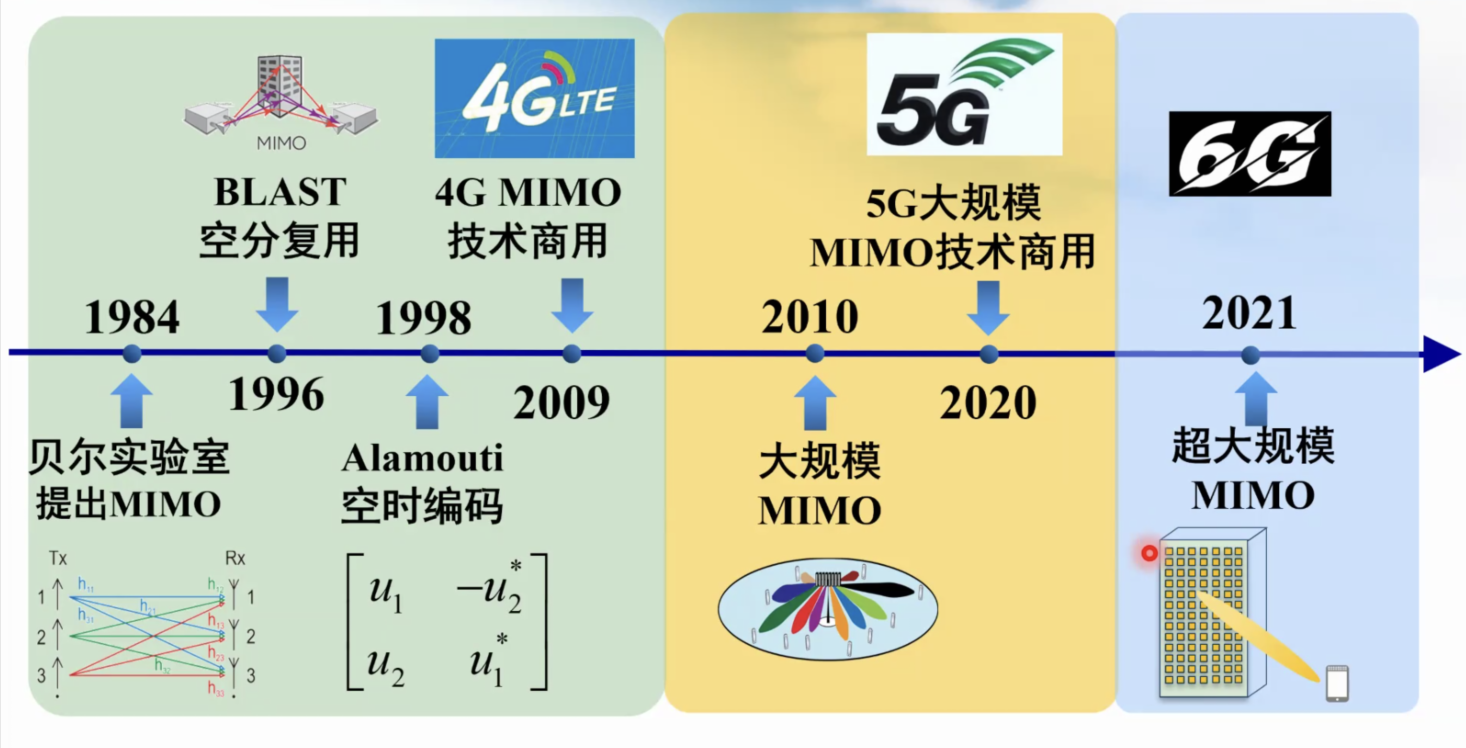
【讲座笔记】Massive MIMO无线通信理论与应用

MIMO无线通信理论与应用暑期学校

2022年7月27日　清华大学电子工程系　戴凌龙

移动通信的核心指标：通信速率每一代提高10倍

MIMO基础

$C=B\log_2(1+SNR)$

代：
- 4G：6~8天线
- 5G：大规模MIMO
- 6G：超大规模MIMO
信息论角度：对称增加基站天线数、用户数，可成倍增加通信速率

$C=\min(M,K)B\log_2(1+SNR)$

其中， $M$ 为基站天线数， $K$ 为用户数
主要特征：
- 提供空间分集：增加天线数量，降低错误概率（SIMO：接收分集，MISO：发射分集）
- 提供空间复用：提供自由度，提供了 $\min(M,K)$ 个并行信道，在高信噪比下有效。

$\mathbf{y}_{N_r}(k)=\mathbf{H}_{N_r\times N_t}(k) \mathbf{x}_{N_t}(k)+\mathbf{n}_{N_r}(k)$

其中， $\mathbf{n}$ 是接收机噪声，非信道噪声。 $N_0=nB=噪声功率谱密度\times 带宽$ 。

奇异值分解：

$\mathbf{H}_{N_r\times N_t}=\mathbf{U}_{N_r\times N_r}\mathbf{\Lambda}_{N_r\times N_t} \mathbf{V}_{N_t\times N_t}$
- 预编码（Precoding）： $\tilde{\mathbf{x}}_{N_t}(k) =\mathbf{V}_{N_t\times N_t}^H\mathbf{x}_{N_t}(k)$ 。
- Combining： $\tilde{\mathbf{y}}_{N_r}(k) =\mathbf{U}_{N_r\times N_r}^H\mathbf{y}_{N_r}(k)$ .
- $N$ 个独立信道： $\tilde{y}_i(k)=\lambda_i \tilde{x}_i(k) + \tilde{n}_i(k)$ ，并行信道数量 $N$ 不大于 $\min(N_t,N_r)$ .
不考虑公平性的信道容量——总发射功率一定约束下，分配 $P_i$ 使下式最大：

$C=\sum_{i=1}^{N}\log_2\left(1+\frac{P_i\lambda_i^2}{N_0}\right)$

注水法（信噪比越低分配愈多的功率）： $P_i=\left(\mu-\frac{N_0}{\lambda_i^2}\right)^+$ ， $\lambda_i$ 是第i个独立信道的奇异值

ZF接收机： $\mathbf{y}$ 乘上 $\mathbf{H}^{\dagger}$ ， $\hat{\mathbf{x}}=\mathbf{H}^\dagger\mathbf{y}$
- 低信噪比，噪声放大
- 无偏估计
MMSE接收机：考虑噪声影响， $\hat{\mathbf{x}}_{MMSE}=\mathbf{Ay}=\mathbf{H}^H(\mathbf{HH}^H+\sigma^2\mathbf{I})^{-1}\mathbf{y}$
- 更好的信噪比性能
- 有偏估计
高信噪比下 $\sigma^2\to 0$ ，ZF和MMSE性能差不多
线性检测劣于非线性检测（最大似然）

发射端多天线，提供空间分集增益
原理：连续两个时间周期里分别从两个发射天线发射

$\begin{array}{lllll} [T_1] & Tx1: & x_1 & Tx2: & x_2\\ [T_2] & Tx1: & -x_2^* & Tx2: & x_1^* \end{array}$
编码矩阵： $X=\begin{bmatrix}x_1 & -x_2^*\\ x_2 & x_1^*\end{bmatrix}$ ，具有正交性
译码：

$\left\{ \begin{array}{l} y_1= h_1x_1+h_2x_2+\eta_1\\ y_2=-h_1x_2^*+h_2x_1^*+\eta_2 \end{array}\right. \Rightarrow \left\{ \begin{array}{l} \hat{x}_1 只含 x_1 \\ \hat{x}_2 只含 x_2 \end{array} \right.$
分集增益（ $|h_1|^2+|h_2|^2$ ）
接收端SNR：降低一半噪声，噪声方差减小。

$SNR_d=\frac{|h_1|^2+|h_2|^2}{2}\frac{E_s}{N_0}$

LTE：R.11前4G，R.12后B4G
- R.8/9：下行OFDMA、多天线技术
- R.10/11：最多8路复用数据，增强多用户MIMO
开环/闭环MIMO：
- 开环MIMO：预编码矩阵确定，与信道状态无关
- 闭环MIMO：预编码矩阵与信道状态有关（LTE/LTE-A）
  - 显式反馈——大量反馈开销
  - 隐式反馈——码本-（码本集合索引PMI）>性能损失（LTE/LTE-A）
接收机：
- MMSE接收机
- 联合最大似然接收机（复杂度指数上升）
多用户MIMO：R.9 最多4路数据流，4个用户

增加 $M,K$ 可以提高频谱效率
- 分集增益 $MK$ ：误码率（可靠性指标） $p_e\sim SNR^{-MK}$
- 复用增益 $\min(M,K)$ ：可达和速率（空分复用） $C=\min(M,K)B\log_2(1+SNR)$

$\mathbf{y}=\sqrt{p}\mathbf{H}\mathbf{x}+\mathbf{n}$

信道模型：大尺度衰落、小尺度衰落
”大规模“：量变->质变——随机矩阵理论

$\left\{ \begin{array}{l} \displaystyle \lim_{M\to\infty,\ i\neq j} \frac1M h_i^Hh_j=0\\ \displaystyle \lim_{M\to \infty} \frac1Mh_i^Hh_i=\sigma^2 \end{array}\right.$
- 多用户信道渐近正交
- 随机信道硬化（特征值逐渐固定）

大规模MIMO中，信道小尺度衰落因随机信道硬化消失，有 $\frac{\mathbf{G}^H\mathbf{G}}{M}=\mathbf{D}$ (对角阵)。

$R=\sum_{k=1}^K\log_2(1+P\lambda_k^2)$

其中，总能量固定( $\sum_{k=1}^K\lambda_k^2=MK$ )，理想传输条件 $\mathbf{H}^H\mathbf{H}=M\mathbf{I}$ 。

速率上限：

$R=K\log_2(1+MP)$

信号检测：已知 $\mathbf{H}$ ，由 $\mathbf{y}$ 求 $\mathbf{x}$ 。

多用户信号检测模型：多用户叠加、干扰，需要区分

$\mathbf{y}_{N\times 1}=h_1x_1+h_2x_2+\cdots+h_kx_k+\mathbf{n}=\mathbf{H}_{N\times K}\mathbf{x}_{K\times 1}+\mathbf{n}_{N\times 1}$

经典算法：

最大似然检测
- 方法：穷搜全部可行解（星座点），找最相似的，即为最优
- 代价：指数复杂度，支持的 $K$ 很小，存在瓶颈
迫零检测（立方复杂度，比最大似然检测好）
- 方法： $\hat{\mathbf{x}}=\mathbf{H}^\dagger\mathbf{y}=\mathbf{x}+(\mathbf{H}^H\mathbf{H})^{-1}\mathbf{H}^H\mathbf{n}$ ， $(\mathbf{H}^H\mathbf{H})^{-1}\mathbf{H}^H\mathbf{n}$ 为等效噪声
- 代价：低信噪比，放大噪声性能损失严重
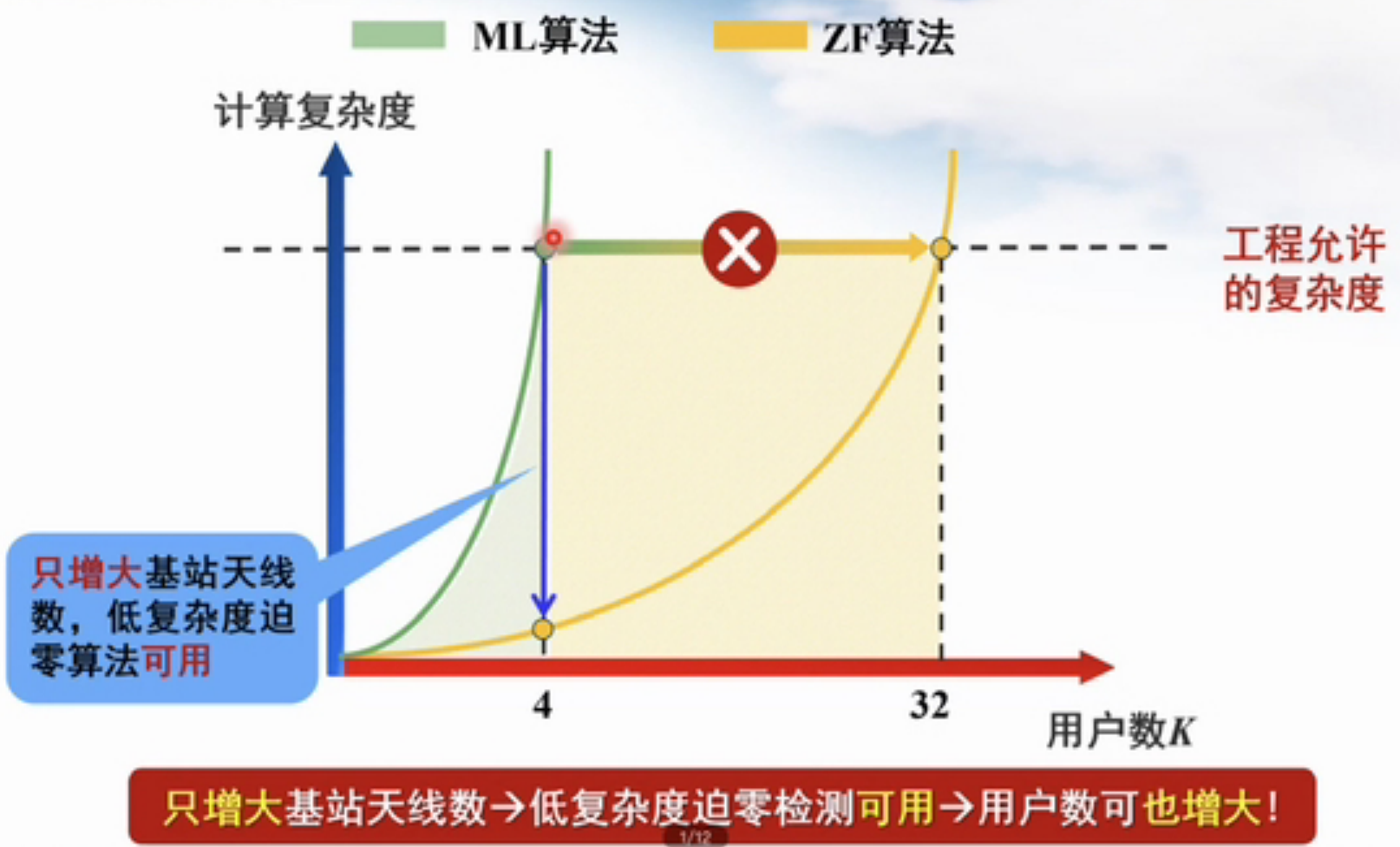
最大似然检测的性能+迫零检测的速度——非对称增加 $M,K$ $M, K$
- 大幅度提升基站天线数（ $K$ 不变，只增大 $M$ ）
- 超定方程容易求解=>观测越多，越容易区分不同用户的信号（ $\mathbf{H}$ 各列干扰小）=>只大幅增加 $M$ ，信道干扰 $\to 0$
- 此时，迫零检测具有准最优性能（噪声放大=>噪声不变）
只增大 $M$ （非对称思想）=>低复杂度ZF可用=>用户数增大（ $M,K$ 同比例增大）

导频开销过高

$\mathbf{y}_{P\times 1}=\mathbf{C}_{P\times M}\mathbf{h}_{M\times 1}+\mathbf{n}_{P\times 1}$

最小二乘法：已知 $\mathbf{y}_{P\times 1},\mathbf{C}_{P\times M}$ 估计 $\mathbf{h}_{M\times 1}$ ，要求方程个数/导频组数 $P\geq$ 未知数个数/天线数 $M$
压缩感知：

$\mathbf{y}_{P\times 1}=\mathbf{A}_{P\times M}\mathbf{s}_{M\times 1}$

天线域信道非稀疏=( $\mathcal{F}$ )=>空间域系统稀疏，令 $\mathbf{A}_{P\times M}=\mathbf{C}_{P\times M}\mathbf{F}_{M\times M}$ ， $\mathbf{s}$ 稀疏，使得 $P<M$ 可行。

信道估计问题=>压缩感知问题

采用隐式反馈，利用”码本“的方式。

反馈位数 $B$ 与发射天线数 $M$ 成正比，反馈码本尺寸随 $M$ 指数增加，存不下！
基于角度域稀疏性的信道反馈方式 $\mathbf{H}_b=\mathbf{U}_R^H\mathbf{H}\mathbf{U}_T$ $H_{b} = U_{R}^{H} H U_{T}$
- 用户反馈低维观测向量 $\mathbf{y}$ 到基站
- 基站利用压缩感知恢复高维信道矩阵 $\hat{\mathbf{s}}$

代
- 4G：2-8天线
- 5G：128天线
- 6G：1024+天线（有源天线阵列、智能超表面RIS）
超大规模MIMO的“质变”——近场宽带效应
- 远场假设（平面波）可能不成立，用户可能分布在近场（球面波），区分点瑞利距离 $\frac{2D^2}{\lambda}$
- 严重的波束分裂，窄带假设可能不成立，变为宽带
近场宽带效应的解决
- 近场信道的分区远场近似（解耦）
- 相移产生窄带平面波，匹配远场相位
  
  时延逼近宽带球面波，补偿近场相位
- 有效Rayleigh条件——波束赋形分集增益定义
  
  经典Rayleigh条件——最大相位误差定义