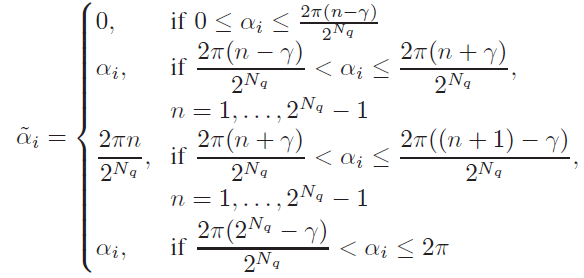由于没有非常系统地看完MIMO的相关内容,整理中必定有很多的问题,欢迎在评论区批评指正。
整理很乱。。。
由于网页公式渲染器KaTeX不支持公式交叉引用,我的前端水平就不足以把我这个模板加入mathjax。故将所有公式交叉引用均删除了,有的是在显示不出来的建议贴到markdown里面去吧
Transfer Learning and Meta Learning-Based Fast Downlink Beamforming Adaptation
提出背景——传统深度学习方法无法很好处理训练集和测试集的mismatch
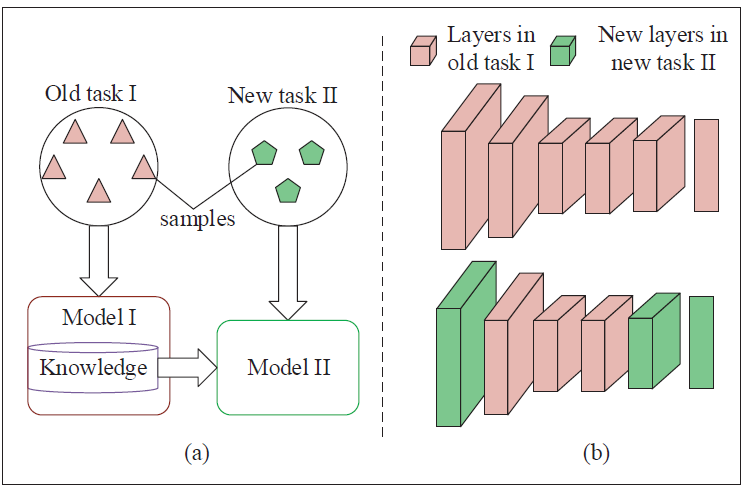
Transfer learning is a promising technique to deal with the task mismatch issue experienced in the practical wireless communication systems due to its ability to transfer the useful prior knowledge to a new scenario [27].
Another efficient way to deal with the task mismatch issue is meta-learning, which aims to improve the learning ability by leveraging
解决的任务——SINR balancing problem under a total power constraint
通过上行链路-下行链路对偶性,可以先求上行链路的功率分配矢量q \mathbf q q
Loss采用MSE
L o s s D ( θ ) = 1 N ∑ i = 1 N ∥ q ^ ( i ) ( θ ) − q ( i ) ∥ 2 2 Loss_{\mathbb{D}}(\theta)=\frac 1N\sum_{i=1}^N\left\|\hat{\mathbf q}^{(i)}(\theta)-{\mathbf q}^{(i)} \right\|_2^2
L o s s D ( θ ) = N 1 i = 1 ∑ N ∥ ∥ ∥ q ^ ( i ) ( θ ) − q ( i ) ∥ ∥ ∥ 2 2
先在分布不同的训练集下训练,再固定前L − 1 L-1 L − 1 L L L
一文入门元学习(Meta-Learning)(附代码) - 知乎 (zhihu.com)
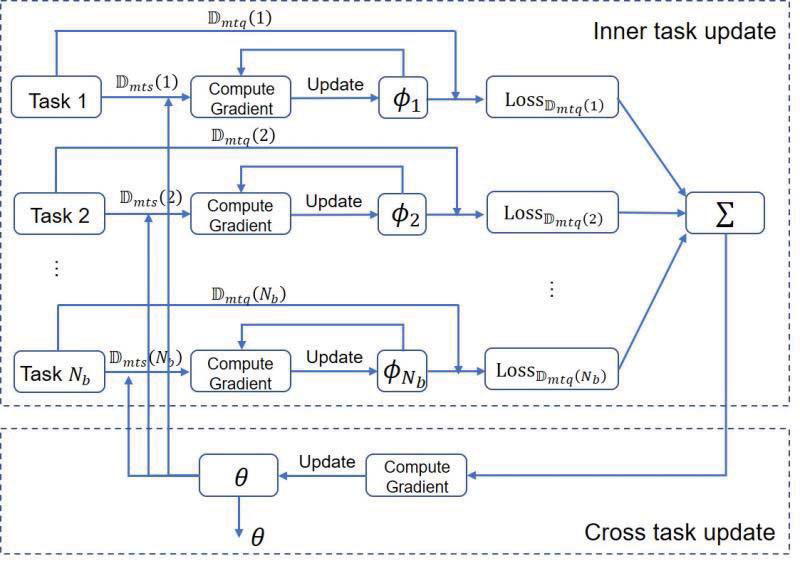
训练阶段
inner-task——在每个任务中计算support set的Loss,并更新任务参数:
ϕ k ( i ) = ϕ k ( i − 1 ) − β ∇ ϕ k ( i − 1 ) L o s s D m t s ( k ) ( ϕ k ( i − 1 ) ) \phi_k^{(i)}=\phi_k^{(i-1)}-\beta\nabla_{\phi_k^{(i-1)}}Loss_{\mathbb{D}_{mts}(k)}\left(\phi_k^{(i-1)}\right)
ϕ k ( i ) = ϕ k ( i − 1 ) − β ∇ ϕ k ( i − 1 ) L o s s D m t s ( k ) ( ϕ k ( i − 1 ) )
第一轮为θ \theta θ ϕ k ( 0 ) \phi_k^{(0)} ϕ k ( 0 )
cross-task——计算各任务query set的Loss的和,更新全局的参数:
θ ← θ − α ∇ θ ∑ k = 1 N b L o s s D m t q ( k ) ( ϕ k ) \theta\leftarrow\theta- \alpha\nabla_\theta \sum_{k=1}^{N_b}Loss_{\mathbb{D}_{mtq}(k)}\left(\phi_k\right)
θ ← θ − α ∇ θ k = 1 ∑ N b L o s s D m t q ( k ) ( ϕ k )
适应阶段
Comparison of Transfer Learning and Meta Leaning : Transfer learning and meta learning both have the training and adaption stages. Although they have the same objective of achieving fast adaption, the strategies used in the training and adaption stages are different. Hence, transfer learning is not a special case of meta learning. Meta learning uses two iterative procedures to train the model, which means that it needs two backward passes in the training stage. However, transfer learning uses one backward pass to train the model in the training stage. In the adaption stage, meta learning re-trains all parameters on the new task whereas transfer learning only re-trains the parameter of the last layer while retaining the rest parameters.
在线学习——解决串行数据
在线meta learning:不重新学习了,从第一个时刻前开始就是通过前面的时间的数据来进行元学习,再通过每次更新的步长计算这一次的
inner-task:——task-specific(16)、(17),第一次通过θ t \theta_t θ t
ϕ k ( j ) = ϕ k ( j − 1 ) − β ∇ ϕ k ( j − 1 ) L o s s D k t r a i n ( ϕ k ( j − 1 ) ) \phi_k^{(j)}=\phi_k^{(j-1)}-\beta\nabla_{\phi_k^{(j-1)}}Loss_{\mathcal{D}_{k}^{train}}\left(\phi_k^{(j-1)}\right)
ϕ k ( j ) = ϕ k ( j − 1 ) − β ∇ ϕ k ( j − 1 ) L o s s D k t r a i n ( ϕ k ( j − 1 ) )
cross-task:——shared network(18)
θ t ← θ t − α ∇ θ ∑ k = 1 t − 1 Z k L o s s D k v a l i d a t i o n ( ϕ k N i n ) \theta_t\leftarrow\theta_t- \alpha\nabla_\theta \sum_{k=1}^{t-1}Z_kLoss_{\mathcal{D}_{k}^{validation}}\left(\phi_k^{N_{in}}\right)
θ t ← θ t − α ∇ θ k = 1 ∑ t − 1 Z k L o s s D k v a l i d a t i o n ( ϕ k N i n )
Z k Z_k Z k T k \mathcal{T}_k T k N i n N_{in} N i n
通过线下学习到的网络参数作为线上学习的初始值
既然要算监督学习的Loss,那么标签也就是真实的上行链路功率分配矢量q \mathbf q q
————online learning是监督学习!!!是有标签的!
the offline algorithm heavily relies on the stationary environment.
DTL(先在分布不同的训练集下训练,再固定普遍特征的层在有限样本的优化集训练全连接层)
MAML(①meta-learning,②fine-tuning)
FTL(解决序列形式的实时系统)、meta-learning(快速自适应)
不需要大量数据和训练,达到near optimal
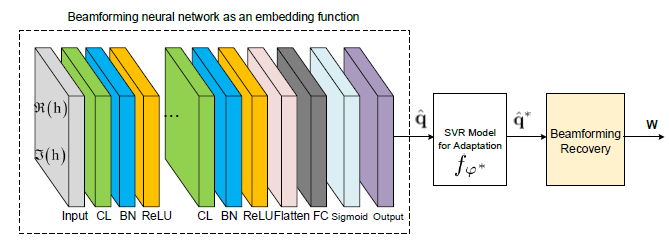
Embedding Model Based Fast Meta Learning for Downlink Beamforming Adaptation
general utility maximization problem under the total power constraint
max W U ( γ 1 , ⋯ , γ K ) s . t . ∑ k = 1 K ∥ w k ∥ 2 2 ≤ P \begin{aligned}
\max_\mathbf W \quad&U(\gamma_1,\cdots,\gamma_K)\\
s.t.\quad&\sum_{k=1}^K\left\|\mathbf w_k\right\|_2^2\le P
\end{aligned}
W max s . t . U ( γ 1 , ⋯ , γ K ) k = 1 ∑ K ∥ w k ∥ 2 2 ≤ P
只关注提取特征,
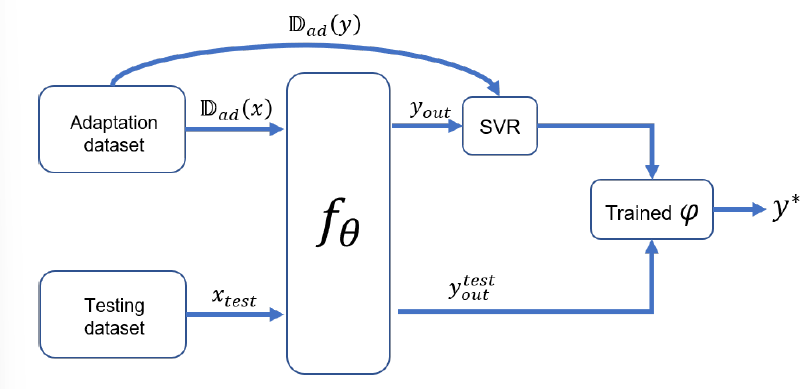
先将所有meta learning的support set和query set构成训练集D f a s t \mathcal{D}_{fast} D f a s t θ \theta θ f θ f_\theta f θ
θ = arg min θ L o s s D f a s t ( θ ) \theta=\arg\min_\theta Loss_{\mathcal{D}_{fast}}(\theta)
θ = arg θ min L o s s D f a s t ( θ )
在D a d a p t \mathbb{D}_{adapt} D a d a p t φ \varphi φ D a d a p t \mathbb{D}_{adapt} D a d a p t D a d a p t ( y ) \mathbb{D}_{adapt}(y) D a d a p t ( y ) y o u t = f θ ( D a d a p t ) y_{out}=f_\theta(\mathbb{D}_{adapt}) y o u t = f θ ( D a d a p t ) f φ ∗ f_{\varphi^*} f φ ∗
φ ∗ = arg min φ L o s s D a d a p t ( y ) ( W y o u t + b , D a d a p t ( y ) ) \varphi^*=\arg\min_\varphi Loss_{\mathbb{D}_{adapt}(y)}(Wy_{out}+b,\mathbb{D}_{adapt}(y))
φ ∗ = arg φ min L o s s D a d a p t ( y ) ( W y o u t + b , D a d a p t ( y ) )
再通过训练得到的f θ f_\theta f θ f φ ∗ f_{\varphi^*} f φ ∗
extracting features from adaptation data of the current time slot; B t \mathcal{B}_t B t
在time shot t t t
q ^ t ∗ = f θ ( B t ( h t ) ) \hat{\mathbf q}_t^*=f_\theta(\mathcal{B}_t(\mathbf h_t))
q ^ t ∗ = f θ ( B t ( h t ) )
将提取到的特征q ^ t ∗ \hat{\mathbf q}_t^* q ^ t ∗ B t \mathcal{B}_t B t q t \mathbf q_t q t
ϕ t = arg min ϕ t L o s s ( W t q ^ t ∗ + b t , B t ( q t ) ) \phi_t=\arg\min_{\phi_t}Loss(\mathbf W_t\hat{\mathbf q}_t^*+\mathbf{b_t},\mathcal{B}_t(\mathbf q_t))
ϕ t = arg ϕ t min L o s s ( W t q ^ t ∗ + b t , B t ( q t ) )
online learning是监督学习!
Knowledge Distillation-Aided End-to-End Learning for Linear Precoding in Multiuser MIMO Downlink Systems With Finite-Rate Feedback ——思路类似【ai5】
在一般的方法中,类似【ai5】都采用了Straight-through estimator。但是伪梯度可能会导致不在正确的方向上更新参数。
本文提出了一种与知识蒸馏(KD)相结合的训练方法,在辅助教师网络的帮助下,通过使用附加的“无损梯度”来有效地训练接收方DNN 。随后,联合执行端到端学习以确定最大化下行链路和速率的预编码矩阵。提出的数据驱动方案优于传统的基于码本的线性预编码方法。
优化问题:最大化速率(下面这个公式感觉有点问题)
R k ≜ E [ log 2 ∣ I N + P M ∑ l = 1 K H k H V l V l H H k ∣ ] − E [ log 2 ∣ I N + P M ∑ l = 1 , l ≠ k K H k H V l V l H H k ∣ ] R_k\triangleq \mathbb{E}\left[\log_2\left|\mathbf{I}_N+\frac PM\sum_{l=1}^{K}\mathbf H_k^H\mathbf V_l\mathbf V_l^H\mathbf H_k \right|\right]-\mathbb{E}\left[\log_2\left|\mathbf{I}_N+\frac PM\sum_{l=1,l\neq k}^{K}\mathbf H_k^H\mathbf V_l\mathbf V_l^H\mathbf H_k \right|\right]
R k ≜ E [ log 2 ∣ ∣ ∣ ∣ ∣ I N + M P l = 1 ∑ K H k H V l V l H H k ∣ ∣ ∣ ∣ ∣ ] − E ⎣ ⎡ log 2 ∣ ∣ ∣ ∣ ∣ ∣ I N + M P l = 1 , l = k ∑ K H k H V l V l H H k ∣ ∣ ∣ ∣ ∣ ∣ ⎦ ⎤
导频估计:
训练导频p l ∈ C M × 1 \mathbf p_l\in \mathbb{C}^{M\times 1} p l ∈ C M × 1
接收信号y l , k t r a i n = P t r a i n H k H p l + n k \mathbf y_{l,k}^{train}=\sqrt{P_{train}}\mathbf H_k^H\mathbf p_l+\mathbf n_k y l , k t r a i n = P t r a i n H k H p l + n k H ˉ \bar{\mathbf H} H ˉ
将信道矩阵进行紧凑形奇异值分解
H ˉ k ⏟ M × N = H ~ k ⏟ M × N Σ k 1 2 ⏟ N × N U k H ⏟ N × N \underbrace{\bar{\mathbf H}_k}_{M\times N}=\underbrace{\tilde{\mathbf H}_k}_{M\times N}\underbrace{\boldsymbol{\Sigma}^{\frac12}_k}_{N\times N}\underbrace{\mathbf{U}_k^H}_{N\times N}
M × N H ˉ k = M × N H ~ k N × N Σ k 2 1 N × N U k H
H ~ \tilde{\mathbf H} H ~ H ~ \tilde{\mathbf H} H ~ H ~ k \tilde{\mathbf H}_k H ~ k Σ k \boldsymbol{\Sigma}_k Σ k
第k k k B B B C k = { A k , 1 , ⋯ , A k , 2 B } \mathcal{C}_k=\{\mathbf A_{k,1},\cdots,\mathbf A_{k,2^B}\} C k = { A k , 1 , ⋯ , A k , 2 B } d ( ∙ , ∙ ) d(\bullet,\bullet) d ( ∙ , ∙ ) q k q_k q k
q k = arg min j ∈ { 1 , ⋯ , 2 B } d ( A k , j , H ~ k ) q_k=\arg\min_{j\in\{1,\cdots,2^B\}}d\left(\mathbf A_{k,j},\tilde{\mathbf H}_k\right)
q k = arg j ∈ { 1 , ⋯ , 2 B } min d ( A k , j , H ~ k )
基站侧通过码本C k \mathcal{C}_k C k H ^ k = A k , q k \hat {\mathbf H}_k=\mathbf A_{k,q_k} H ^ k = A k , q k
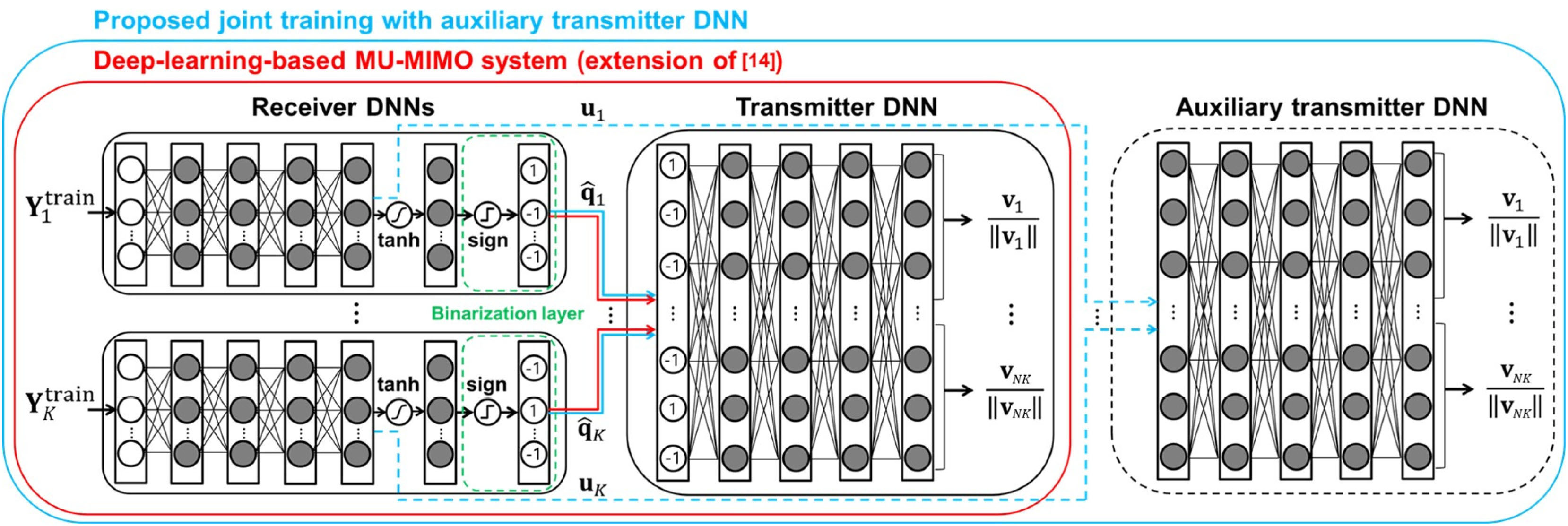
接收机DNN:——全连接网络的激活函数采用ReLU
q ^ k = f k R x ( Y k t r a i n , Θ k R x ) = sign ( tanh ( F C k R x ( r k R e , Θ k R x ) ) ) = [ sign ( tanh ( [ u k ] 1 ) ) , … , sign ( tanh ( [ u k ] B ) ) ] \begin{aligned}
\hat{\mathbf{q}}_{k} &=f_{k}^{\mathrm{Rx}}\left(\mathbf{Y}_{k}^{\mathrm{train}}, \boldsymbol\Theta_{k}^{\mathrm{Rx}}\right)=\operatorname{sign}\left(\tanh \left(\mathrm{FC}_{k}^{\mathrm{Rx}}\left(\mathbf{r}_{k}^{\mathrm{Re}}, \boldsymbol\Theta_{k}^{\mathrm{Rx}}\right)\right)\right) \\
&=\left[\operatorname{sign}\left(\tanh \left(\left[\mathbf{u}_{k}\right]_{1}\right)\right), \ldots, \operatorname{sign}\left(\tanh \left(\left[\mathbf{u}_{k}\right]_{B}\right)\right)\right]
\end{aligned}
q ^ k = f k R x ( Y k t r a i n , Θ k R x ) = s i g n ( tanh ( F C k R x ( r k R e , Θ k R x ) ) ) = [ s i g n ( tanh ( [ u k ] 1 ) ) , … , s i g n ( tanh ( [ u k ] B ) ) ]
其中,
r k R e \mathbf r_k^{Re} r k R e Y k t r a i n \mathbf Y_k^{train} Y k t r a i n Θ k R x \boldsymbol{\Theta}_k^{Rx} Θ k R x u k \mathbf u_k u k B B B
发射机DNN:
V = [ V 1 , ⋯ , V K ] = f T x ( q ^ 1 , ⋯ , q ^ K , P ; Θ T x ) = h ( F C T x ( q 1 ^ , ⋯ , q K ^ , P ; Θ T x ) ) \begin{aligned}
\mathbf V=[\mathbf V_1,\cdots,\mathbf V_K]&=f^{Tx}(\hat{\mathbf q}_1,\cdots,\hat{\mathbf q}_K,P;\boldsymbol{\Theta}^{Tx})\\
&=h(FC^{Tx}(\hat{\mathbf q_1},\cdots,\hat{\mathbf q_K},P;\boldsymbol{\Theta}^{Tx}))
\end{aligned}
V = [ V 1 , ⋯ , V K ] = f T x ( q ^ 1 , ⋯ , q ^ K , P ; Θ T x ) = h ( F C T x ( q 1 ^ , ⋯ , q K ^ , P ; Θ T x ) )
其中,h h h 2 M N K 2MNK 2 M N K M × N K M\times NK M × N K
Loss:
L main ( { Θ k R x } k = 1 K , Θ T x ) = − ∑ k = 1 K R k ( f T x ( { f k R x ( Y k t r a i n ; Θ k R x ) } k = 1 K , P ; Θ T x ) ) . \begin{aligned}
&L_{\operatorname{main}}\left(\left\{\boldsymbol\Theta_{k}^{\mathrm{Rx}}\right\}_{k=1}^{K}, \boldsymbol\Theta^{\mathrm{Tx}}\right) \\
&\quad=-\sum_{k=1}^{K} R_{k}\left(f^{\mathrm{Tx}}\left(\left\{f_{k}^{\mathrm{Rx}}\left(\mathbf{Y}_{k}^{\mathrm{train}} ; \boldsymbol\Theta_{k}^{\mathrm{Rx}}\right)\right\}_{k=1}^{K}, P ; \boldsymbol\Theta^{\mathrm{Tx}}\right)\right) .
\end{aligned}
L m a i n ( { Θ k R x } k = 1 K , Θ T x ) = − k = 1 ∑ K R k ( f T x ( { f k R x ( Y k t r a i n ; Θ k R x ) } k = 1 K , P ; Θ T x ) ) .
优化目标:
min Θ T x , Θ 1 R x , … , Θ K R x L main ( { Θ k R x } k = 1 K , Θ T x ) \min _{\boldsymbol\Theta^{\mathrm{Tx}}, \boldsymbol\Theta_{1}^{\mathrm{Rx}}, \ldots, \boldsymbol\Theta_{K}^{\mathrm{Rx}}} L_{\operatorname{main}}\left(\left\{\boldsymbol\Theta_{k}^{\mathrm{Rx}}\right\}_{k=1}^{K}, \boldsymbol\Theta^{\mathrm{Tx}}\right)
Θ T x , Θ 1 R x , … , Θ K R x min L m a i n ( { Θ k R x } k = 1 K , Θ T x )
反向传播:注意到二值化无法反向传播,常见的方法是采用直通(STE) ,本文中类似【KD-14】考虑到双曲正切函数的性质
∇ Θ k R s i g n ( tanh ( z ) ) ≈ ∇ Θ k R tanh ( z ) \nabla_{\Theta_k^R}\ \mathrm{sign}(\tanh(z))\approx\nabla_{\Theta_k^R}\tanh(z)
∇ Θ k R s i g n ( tanh ( z ) ) ≈ ∇ Θ k R tanh ( z )
但是上述方法的噪声积累仍会导致DNN参数梯度下降方向不正确,表现变差,故最好的方式是将“损失更小的梯度”反向传播给接收机DNN,于是就引出了KD 。The best solution to overcome the noisy gradient problems is to provide “lossless gradients” to receiver DNNs. To achieve this, we propose a novel joint training method using KD.
因为有一个二值化,所以要用STE才能反向传播,但这样就会累计误差,所以把辅助发射机DNN在还没有二值化的地方,先训练“接收机DNN+辅助发射机DNN”再训练“接收机DNN+发射机DNN”
在接收机DNNs的末端只有一个瓶颈(二进制层)。换言之,浅层学生网络(原始发射机DNN)和深层教师网络(辅助发射机DNN)具有相同的结构,除了tanh函数和二值化层(tanh层和二值化层都不用于深层教师网络,因为它们导致梯度消失问题)。
可以看作是【ai2】【ai3】的介绍
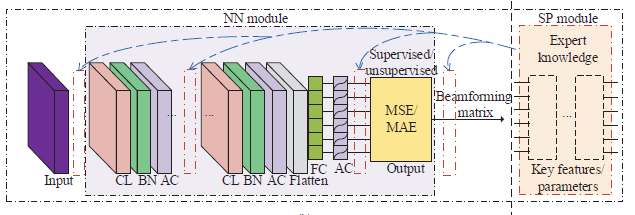
两类BNN网络框架(architecture):
data-based:看称黑箱(black-box) blind to any specialized signal structures , does not have the same computational efficiency, and the performance is often inferior to that of traditional SP methods .
model-based: Inside the SP module are the functional layers that are designed according to prior expert knowledge of beamforming problems , which is problem-specific and has no unified form. It is also possible to replace one or more layers in the ordinary NN module by the SP module to achieve better feature extraction ability.——【ai2】
监督学习/无监督学习
监督学习:适应于存在最优解算法、易于获得标签的问题,常采用MSE/MAE Loss——【ai2】中的P1(功率约束下SINR balancing)、P2(Qos下功率最小)
无监督学习:不存在最优解算法,采用目标函数作为Loss——【ai2】中的P3(功率约束下SR最大)、【ai3】中的单天线约束下SINR balancing
混合(Hybrid):类似【ai2】中对于P3的训练方式,两阶段,先监督逼近WMMSE,后无监督用SR作为Loss
复杂度
优化问题复杂度:【ai2】通过model-based的引入,不直接输出波束形成矩阵,而先输出一些关键特征,如上行/下行链路的功率分配矢量
NN模块的复杂度:冗余的神经元——为了降低神经网络模块的复杂度,我们可以首先使用边缘检测来剪除所有权值在一定阈值以下的连接和那些具有零激活神经元的连接。然后,我们通过压缩技术减少用于表示每个权重的比特数,并在不同的连接之间实施权重分担以减少权重的数量。最后,可以采用霍夫曼编码来使用具有更少比特的符号来表示更多的公共权重[11]。
泛化能力——【ai3】中提及
training-set augmentation:难以获取大量的数据
transfer learning:fine-tuning
open issue
现实环境的数据集
对可能导致BNN训练不一致和失败的损坏数据具有鲁棒性
SU-MIMO
unconstrained SVD
y = R H H T s + R H n \mathbf y=\mathbf R^H\mathbf{HTs}+\mathbf R^H\mathbf n
y = R H H T s + R H n
achieved rate:
R = log 2 ( ∣ I + P L C n − 1 R o p t H H T o p t T o p t H H H R o p t ∣ ) R=\log_2\left(\left|\mathbf I+\frac PL\mathbf C_n^{-1}\mathbf R_{opt}^H\mathbf {HT}_{opt}\mathbf T_{opt}^H \mathbf H^H\mathbf R_{opt}\right|\right)
R = log 2 ( ∣ ∣ ∣ ∣ I + L P C n − 1 R o p t H H T o p t T o p t H H H R o p t ∣ ∣ ∣ ∣ )
其中,T o p t = V L ∈ C N T × L , R o p t = U L ∈ C N R × L , \mathbf T_{opt}=\mathbf V_L\in\mathbb C^{N_T\times L},\mathbf R_{opt}=\mathbf U_L\in\mathbb C^{N_R\times L}, T o p t = V L ∈ C N T × L , R o p t = U L ∈ C N R × L , C = R o p t H R o p t \mathbf C=\mathbf R_{opt}^H\mathbf R_{opt} C = R o p t H R o p t
constrained SVD
y = R B B H R R F H H T R F T B B s + R B B H R R F H n \mathbf y=\mathbf R_{BB}^H\mathbf R_{RF}^H\mathbf{HT}_{RF}\mathbf T_{BB}\mathbf{s}+\mathbf R_{BB}^H\mathbf R_{RF}^H\mathbf n
y = R B B H R R F H H T R F T B B s + R B B H R R F H n
约束条件:
发射信号假设:E [ s s H ] = P L I L \mathbb{E}[\mathbf {ss}^H]=\frac PL\mathbf I_L E [ s s H ] = L P I L
恒模约束:∣ [ T R F ] i , j ∣ 2 = N T − 1 , ∣ [ R R F ] i , j ∣ 2 = N R − 1 , \left|[\mathbf T_{RF}]_{i,j}\right|^2=N_T^{-1},\left|[\mathbf R_{RF}]_{i,j}\right|^2=N_R^{-1}, ∣ [ T R F ] i , j ∣ 2 = N T − 1 , ∣ [ R R F ] i , j ∣ 2 = N R − 1 ,
移相量化:第n n n m m m N q N_q N q e j 2 π n k q N q ( e j 2 π m k q N q ) e^{\frac{j2\pi nk_q}{N_q}}(e^{\frac{j2\pi mk_q}{N_q}}) e N q j 2 π n k q ( e N q j 2 π m k q ) k q = 0 , 1 , ⋯ , 2 N q − 1 k_q=0,1,\cdots,2^{N_q}-1 k q = 0 , 1 , ⋯ , 2 N q − 1
功率约束:∥ T R F T B B ∥ F 2 = L , ∥ R R F R B B ∥ F 2 = L \left\|\mathbf{T}_{RF}\mathbf{T}_{BB}\right\|^2_F=L,\left\|\mathbf{R}_{RF}\mathbf{R}_{BB}\right\|^2_F=L ∥ T R F T B B ∥ F 2 = L , ∥ R R F R B B ∥ F 2 = L
H k = U k Σ k V k H \mathbf H_k=\mathbf U_k\mathbf \Sigma_k\mathbf V_k^H
H k = U k Σ k V k H
写成秩1近似的和
H k = ∑ i = 1 k σ i u i v i \mathbf H_k=\sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i
H k = i = 1 ∑ k σ i u i v i
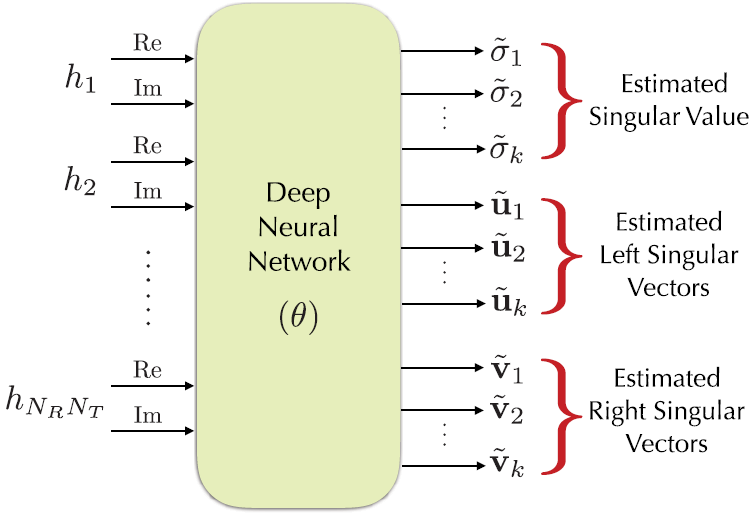
k Matrix Approximation
Loss函数:
L ( θ ) = ∥ H k − H ~ k ∥ F ∥ H k ∥ F + λ 1 ∑ i ≠ j ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 ∑ i ≠ j ∥ v ~ i ∗ v ~ j ∥ 2 \mathcal{L}(\theta)=\frac{\left\|\mathbf{H}_{k}-\tilde{\mathbf{H}}_{k}\right\|_{F}}{\left\|\mathbf{H}_{k}\right\|_{F}}+\lambda_{1} \sum_{i \neq j}\left\|\tilde{\mathbf{u}}_{i}^{*} \tilde{\mathbf{u}}_{j}\right\|_{2}+\lambda_{2} \sum_{i \neq j}\left\|\tilde{\mathbf{v}}_{i}^{*} \tilde{\mathbf{v}}_{j}\right\|_{2}
L ( θ ) = ∥ H k ∥ F ∥ ∥ ∥ H k − H ~ k ∥ ∥ ∥ F + λ 1 i = j ∑ ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 i = j ∑ ∥ v ~ i ∗ v ~ j ∥ 2
(信道矩阵H \mathbf H H
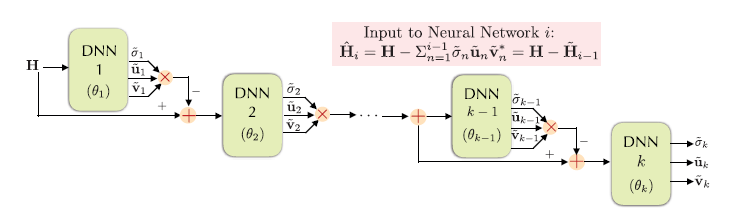
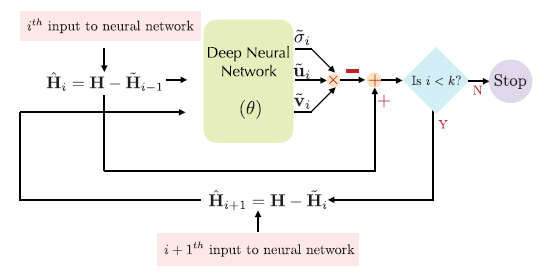
k Matrix Approximation每次求当前最大的奇异值、奇异矩阵,下一次减掉它
trained jointly
L ( θ 1 , θ 2 , ⋯ , θ k ) = ∥ H k − H ~ k ∥ F ∥ H k ∥ F + λ 1 ∑ i ≠ j ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 ∑ i ≠ j ∥ v ~ i ∗ v ~ j ∥ 2 \mathcal{L}(\theta_1,\theta_2,\cdots,\theta_k)=\frac{\left\|\mathbf{H}_{k}-\tilde{\mathbf{H}}_{k}\right\|_{F}}{\left\|\mathbf{H}_{k}\right\|_{F}}+\lambda_{1} \sum_{i \neq j}\left\|\tilde{\mathbf{u}}_{i}^{*} \tilde{\mathbf{u}}_{j}\right\|_{2}+\lambda_{2} \sum_{i \neq j}\left\|\tilde{\mathbf{v}}_{i}^{*} \tilde{\mathbf{v}}_{j}\right\|_{2}
L ( θ 1 , θ 2 , ⋯ , θ k ) = ∥ H k ∥ F ∥ ∥ ∥ H k − H ~ k ∥ ∥ ∥ F + λ 1 i = j ∑ ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 i = j ∑ ∥ v ~ i ∗ v ~ j ∥ 2
sequence(θ 1 \theta_1 θ 1
L ( θ i ) = ∥ σ i u i v i ∗ − σ ~ i u ~ i v ~ i ∗ ∥ F ∥ σ i u i v i ∗ ∥ F + λ 1 ∑ i , j < i ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 ∑ i , j < i ∥ v ~ i ∗ v ~ j ∥ 2 \mathcal{L}\left(\theta_{i}\right)=\frac{\left\|\sigma_{i} \mathbf{u}_{i} \mathbf{v}_{i}^{*}-\tilde{\sigma}_{i} \tilde{\mathbf{u}}_{i} \tilde{\mathbf{v}}_{i}^{*}\right\|_{F}}{\left\|\sigma_{i} \mathbf{u}_{i} \mathbf{v}_{i}^{*}\right\|_{F}}+\lambda_{1} \sum_{i, j<i}\left\|\tilde{\mathbf{u}}_{i}^{*} \tilde{\mathbf{u}}_{j}\right\|_{2} +\lambda_{2} \sum_{i, j<i}\left\|\tilde{\mathbf{v}}_{i}^{*} \tilde{\mathbf{v}}_{j}\right\|_{2}
L ( θ i ) = ∥ σ i u i v i ∗ ∥ F ∥ σ i u i v i ∗ − σ ~ i u ~ i v ~ i ∗ ∥ F + λ 1 i , j < i ∑ ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 i , j < i ∑ ∥ v ~ i ∗ v ~ j ∥ 2
采用梯度下降更新参数
将低复杂度Rank-k 的k k k k k k
Loss函数:
L ( θ ) = ∥ H k − H ~ k ∥ F ∥ H k ∥ F + λ 1 ∑ i ≠ j ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 ∑ i ≠ j ∥ v ~ i ∗ v ~ j ∥ 2 \mathcal{L}(\theta)=\frac{\left\|\mathbf{H}_{k}-\tilde{\mathbf{H}}_{k}\right\|_{F}}{\left\|\mathbf{H}_{k}\right\|_{F}}+\lambda_{1} \sum_{i \neq j}\left\|\tilde{\mathbf{u}}_{i}^{*} \tilde{\mathbf{u}}_{j}\right\|_{2}+\lambda_{2} \sum_{i \neq j}\left\|\tilde{\mathbf{v}}_{i}^{*} \tilde{\mathbf{v}}_{j}\right\|_{2}
L ( θ ) = ∥ H k ∥ F ∥ ∥ ∥ H k − H ~ k ∥ ∥ ∥ F + λ 1 i = j ∑ ∥ u ~ i ∗ u ~ j ∥ 2 + λ 2 i = j ∑ ∥ v ~ i ∗ v ~ j ∥ 2
在该方法中,我们不是直接最大化速率,而是最小化无约束波束形成器和混合波束形成器获得的秩-k近似 之间的Frobenius距离(?)。
【理解】
y = R B B H R R F H H T R F T B B s + R B B H R R F H n \mathbf y=\mathbf R_{BB}^H\mathbf R_{RF}^H\mathbf{HT}_{RF}\mathbf T_{BB}\mathbf{s}+\mathbf R_{BB}^H\mathbf R_{RF}^H\mathbf n\\
y = R B B H R R F H H T R F T B B s + R B B H R R F H n
对信道矩阵作SVD,
H = U Σ V H \mathbf H=\mathbf{U\Sigma V^H}
H = U Σ V H
只要让
\mathbf R_{BB}^H\mathbf R_{RF}^H=\mathbf U^H,
\mathbf{T}_{RF}\mathbf T_{BB}=\mathbf V\label{eq:123}
因为Σ \mathbf \Sigma Σ
y = Σ s + U H n \mathbf y=\mathbf \Sigma \mathbf s+\mathbf U^H \mathbf n
y = Σ s + U H n
即上述网络想实现\eqref{eq:123}的近似相等,以保证实现并行信道。同时接近的U , V \mathbf{U,V} U , V
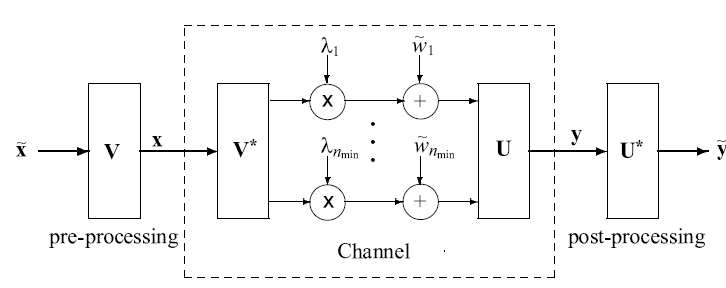
RF预编码恒模约束的四种方法
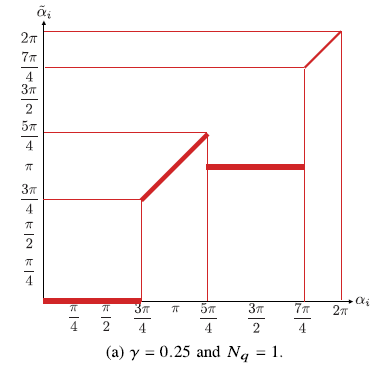
训练阶段,使用分段线性函数的组合来近似均匀量化。
α ~ i = 2 π n 2 N q \tilde\alpha_i=\frac{2\pi n}{2^{N_q}}
α ~ i = 2 N q 2 π n
γ = 0 \gamma=0 γ = 0
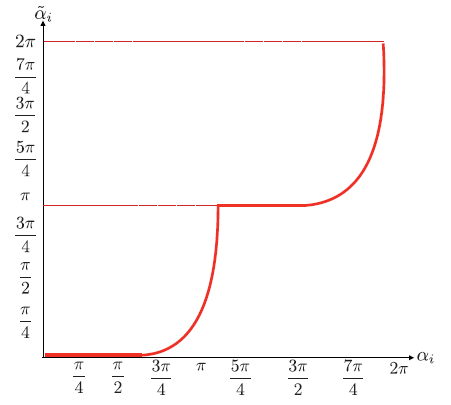
法一存在间断点,不平滑->利用sigmoid函数
α ~ i = 1 1 = exp ( β ( α i − b n ) ) + o n \tilde\alpha_i=\frac{1}{1=\exp(\beta(\alpha_i-b_n))}+o_n
α ~ i = 1 = exp ( β ( α i − b n ) ) 1 + o n
其中,n = 1 , ⋯ , 2 N q n=1,\cdots,2^{N_q} n = 1 , ⋯ , 2 N q b n b_n b n o n o_n o n
在前向传播中,我们使用阶跃函数来应用均匀量化。在反向传播过程中,我们使用Sigmoid函数的线性组合。
在前向传播期间实现随机量化方法,
α ~ i = ⌊ 2 N q α i ⌋ 2 N q + r i 2 N q \tilde{\alpha}_{i}=\frac{\left\lfloor 2^{N_{q}} \alpha_{i}\right\rfloor}{2^{N_{q}}}+\frac{r_{i}}{2^{N_{q}}}
α ~ i = 2 N q ⌊ 2 N q α i ⌋ + 2 N q r i
而在反向传播期间用直通估计器替换。
∂ Q ( α ) i α ~ j = { 1 , α i 被量化到 α ~ j 0 , o t h e r w i s e \frac{\partial Q(\alpha)_i}{\tilde\alpha_j}=\left\{\begin{array}{ll}1,&\alpha_i\text{被量化到$\tilde \alpha_j$}\\
0,&otherwise\end{array}\right.
α ~ j ∂ Q ( α ) i = { 1 , 0 , α i 被量化到 α ~ j o t h e r w i s e
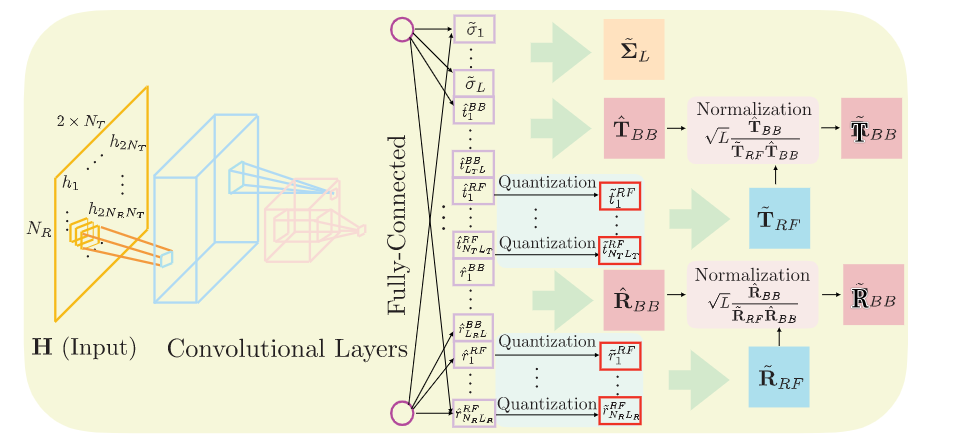
功率约束
用未归一的T ^ B B , R ^ B B \hat{\mathbf T}_{BB},\hat{\mathbf R}_{BB} T ^ B B , R ^ B B T ~ R F , R ~ R F \tilde{\mathbf T}_{RF},\tilde{\mathbf R}_{RF} T ~ R F , R ~ R F
T ~ B B = L T ^ B B ∥ T ~ R F T ^ B B ∥ F R ~ B B = L T ^ B B ∥ R ~ R F R ^ B B ∥ F \begin{aligned}
\tilde{\mathbf T}_{BB}=\sqrt{L}\frac{\hat{\mathbf T}_{BB}}{\left\|\tilde{\mathbf T}_{RF}\hat{\mathbf T}_{BB}\right\|_F}\\
\tilde{\mathbf R}_{BB}=\sqrt{L}\frac{\hat{\mathbf T}_{BB}}{\left\|\tilde{\mathbf R}_{RF}\hat{\mathbf R}_{BB}\right\|_F}
\end{aligned}
T ~ B B = L ∥ ∥ ∥ T ~ R F T ^ B B ∥ ∥ ∥ F T ^ B B R ~ B B = L ∥ ∥ ∥ R ~ R F R ^ B B ∥ ∥ ∥ F T ^ B B
Loss函数: ——L L L L L L
L ( θ ) = ∥ H L − H ~ L ∥ F ∥ H L ∥ F + λ 1 ∑ i ≠ j ∥ r ~ i ∗ r ~ j ∥ 2 + λ 2 ∑ i ≠ j ∥ t ~ i ∗ t ~ j ∥ 2 \mathcal{L}(\theta)=\frac{\left\|\mathbf{H}_{L}-\tilde{\mathbf{H}}_{L}\right\|_{F}}{\left\|\mathbf{H}_{L}\right\|_{F}}+\lambda_{1} \sum_{i \neq j}\left\|\tilde{\mathbf{r}}_{i}^{*} \tilde{\mathbf{r}}_{j}\right\|_{2}+\lambda_{2} \sum_{i \neq j}\left\|\tilde{\mathbf{t}}_{i}^{*} \tilde{\mathbf{t}}_{j}\right\|_{2}
L ( θ ) = ∥ H L ∥ F ∥ ∥ ∥ H L − H ~ L ∥ ∥ ∥ F + λ 1 i = j ∑ ∥ r ~ i ∗ r ~ j ∥ 2 + λ 2 i = j ∑ ∥ ∥ t ~ i ∗ t ~ j ∥ ∥ 2
r ~ i \tilde{\mathbf r}_i r ~ i R ~ o p t \tilde{\mathbf R}_{opt} R ~ o p t t ~ i \tilde{\mathbf t}_i t ~ i T ~ o p t \tilde{\mathbf T}_{opt} T ~ o p t
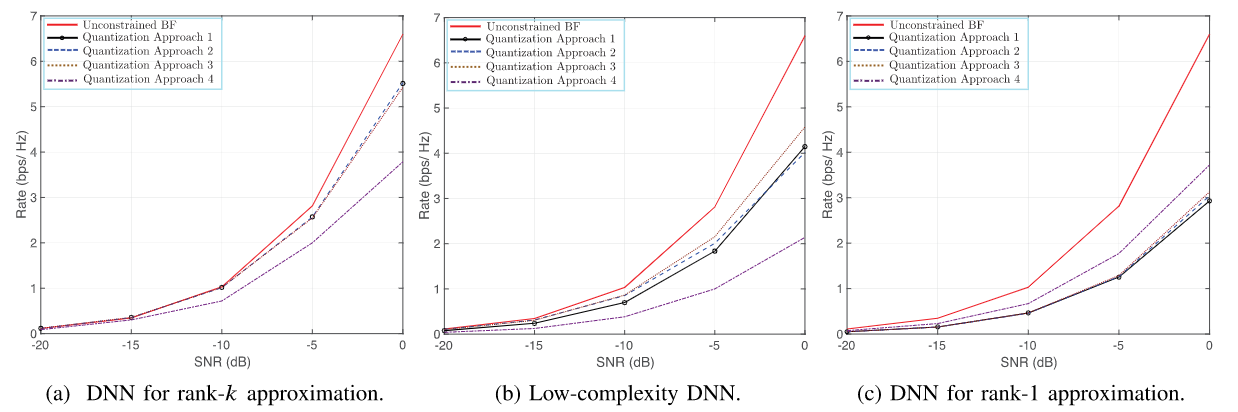
对于不同规模的毫米波系统,基于DNN的混合BF方法用于秩-k矩阵近似的性能优于基于低复杂度DNN的混合BF方法(用于秩k近似)和基于DNN的混合BF方法(用于秩1近似)。——低复杂度秩-k和秩-1的方法在估计后续奇异值、奇异向量时用了之前预测的结果,会带来积累误差。由于在这些仿真中我们考虑满秩信道矩阵,发射和接收天线的数目等于信道的秩,这导致天线数目越多,性能差距越大。
图18-a显示了基于DNN的混合BF用于秩-k矩阵近似时的实现速率,我们观察到当使用DNN用于秩-k矩阵近似时,第一和第二量化方法获得了相似的速率并且优于其他量化方法。在18-b中表明,第三种量化方法以用于秩-k矩阵近似的低复杂度DNN获得了最高的数据速率。我们在18-c中观察到,当使用秩1矩阵的DNN近似时,第四量化方法优于其他方法。
三种DNN结构
第一种体系结构使用单个DNN的矩阵预测给定的k个最重要的奇异值和奇异向量。利用奇异值分解(SVD)的结构,提出了一种低复杂度的秩-k矩阵逼近DNN结构。
第二种结构由k个低复杂度DNN组成,每个DNN被训练来估计给定矩阵的最大奇异值和相应的右、左奇异向量。
为了进一步简化奇异值分解运算,我们提出了秩1矩阵逼近的第三种结构,它使用单个DNN递归地估计k个奇异值和奇异向量。
我们引入了定制的损失函数来训练三种DNN结构,原则上训练DNN的目的是最小化矩阵的真实值和估计秩-k近似之间的Frobenius距离,同时强制奇异向量正交。
四种量化方法
在第一种方法中,我们使用步长和分段线性函数的组合来近似相位量化操作,这在训练过程中提供了非零梯度。
在第二种方法中,我们考虑在前向和后向传播过程中使用几个具有不同参数的Sigmoid函数的组合来进行软量子化。
在第三种方法中,我们在前向传播中使用阶跃函数,而在后向传播中结合不同参数的Sigmoid函数。
在第四种方法中,我们在前向传播期间实现随机量化方法[37],而在反向传播期间用直通估计器[38]替换。
最后,在所提出的DNN体系结构中,我们通过归一化层满足功率约束。

![image-20211130165712424]()



![image-20211202111717068]()
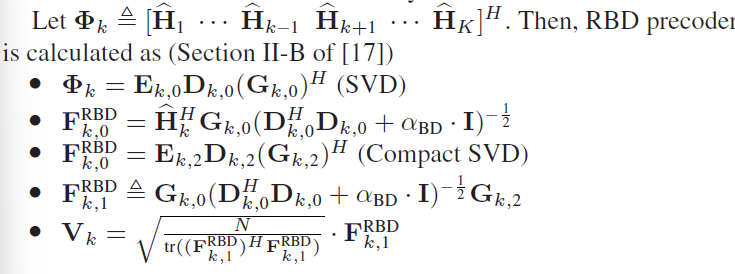

![image-20211209102042438]()
![image-20211209110800360]()
![image-20211214135127640]()
![image-20211214135323497]()
![image-20211214135802275]()
![image-20211214150104362]()