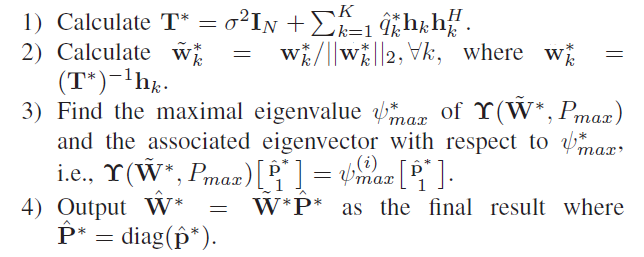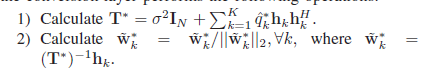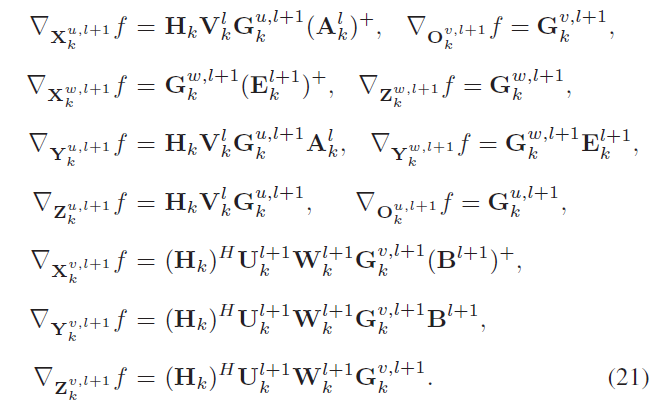由于没有非常系统地看完MIMO的相关内容,整理中必定有很多的问题,欢迎在评论区批评指正。
整理很乱。。。
由于网页公式渲染器KaTeX不支持公式交叉引用,我的前端水平就不足以把我这个模板加入mathjax。故将所有公式交叉引用均删除了,有的是在显示不出来的建议贴到markdown里面去吧
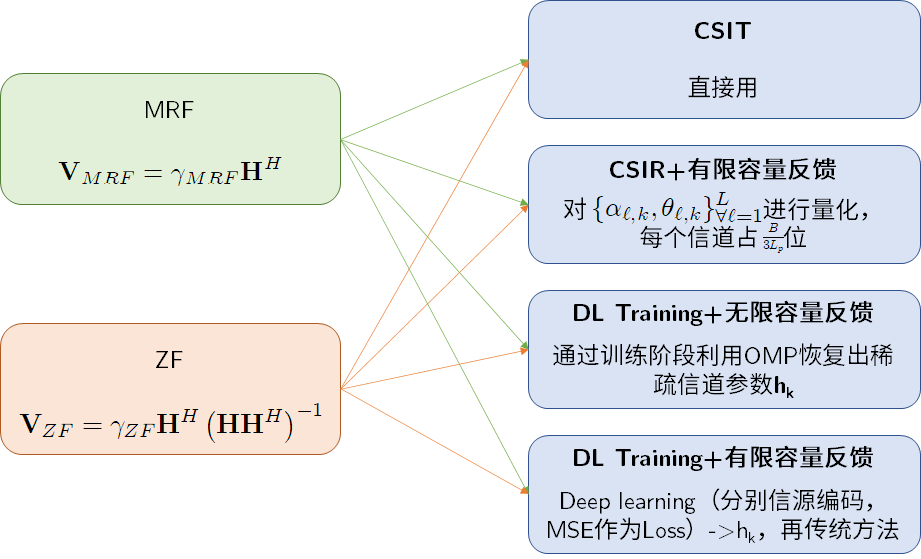
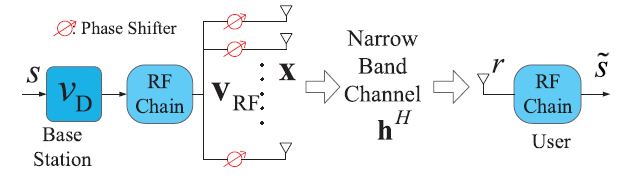
MISO-mmWave——maximizing the spectral efficiency (SE) with hardware limitation and imperfect CSI.
r = h H v R F s + n r=\mathbf{h}^H\mathbf{v}_{RF}s+n
r = h H v R F s + n
其中,v R F ∈ C N t × 1 \mathbf{v}_{RF}\in\mathbb{C}^{N_t\times 1} v R F ∈ C N t × 1
信道矩阵:
h H = N t L ∑ l = 1 L α l a t H ( ϕ t l ) \mathbf{h}^{H}=\sqrt{\frac{N_{\mathrm{t}}}{L}} \sum_{l=1}^{L} \alpha_{l} \mathbf{a}_{\mathrm{t}}^{H}\left(\phi_{\mathrm{t}}^{l}\right)
h H = L N t l = 1 ∑ L α l a t H ( ϕ t l )
其中,L L L l = 1 l=1 l = 1
优化问题——sum-rate problem
max v R F log 2 ( 1 + γ N t ∥ h H v R F ∥ 2 ) s.t. ∣ [ v R F ] i ∣ 2 = 1 , for i = 1 , … , N t , \begin{aligned}
\underset{\mathbf{v}_{\mathrm{RF}}}{\operatorname{max}} \quad & \log _{2}\left(1+\frac{\gamma}{N_{\mathrm{t}}}\left\|\mathbf{h}^{H} \mathbf{v}_{\mathrm{RF}}\right\|^{2}\right) \\
\text { s.t. } \quad &\left|\left[\mathbf{v}_{\mathrm{RF}}\right]_{i}\right|^{2}=1, \quad \text { for } i=1, \ldots, N_{\mathrm{t}},
\end{aligned}
v R F m a x s.t. log 2 ( 1 + N t γ ∥ ∥ h H v R F ∥ ∥ 2 ) ∣ [ v R F ] i ∣ 2 = 1 , for i = 1 , … , N t ,
γ = P σ 2 \gamma=\frac{P}{\sigma^2} γ = σ 2 P v D = P N t v_D=\sqrt{\frac{P}{N_t}} v D = N t P
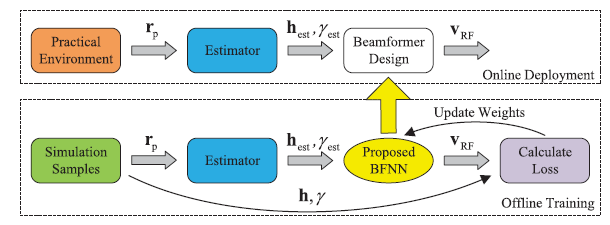
通过估计的h e s t , γ e s t \mathbf{h}_{est},\gamma_{est} h e s t , γ e s t v R F \mathbf{v}_{RF} v R F γ e s t = γ \gamma_{est}=\gamma γ e s t = γ
离线训练:随机生成信道 (可以获得perfect CSI),输入估计的h e s t \mathbf{h}_{est} h e s t v R F \mathbf{v}_{RF} v R F v R F \mathbf{v}_{RF} v R F
在线部署:实际环境信道(imperfect CSI)估计出h e s t , γ e s t \mathbf{h}_{est},\gamma_{est} h e s t , γ e s t v R F \mathbf{v}_{RF} v R F
输入:N t = 64 N_t=64 N t = 6 4 N t = 64 N_t=64 N t = 6 4 h e s t \mathbf{h}_{est} h e s t γ e s t \gamma_{est} γ e s t ( 2 N t + 1 ) × 1 (2N_t+1)\times 1 ( 2 N t + 1 ) × 1
每层开始前先做Batch-Norm
最后输出前通过Lambda层将其变成符合恒模约束的复数矢量v R F \mathbf{v}_{RF} v R F α i ∈ ( 0 , 1 ) \alpha_i\in(0,1) α i ∈ ( 0 , 1 )
v R F = exp ( j 2 π α ) = cos ( 2 π α ) + j sin ( 2 π α ) \mathbf{v}_{RF}=\exp(j2\pi\boldsymbol{\alpha})=\cos(2\pi\boldsymbol{\alpha})+j\sin(2\pi\boldsymbol{\alpha})
v R F = exp ( j 2 π α ) = cos ( 2 π α ) + j sin ( 2 π α )
Loss函数:越小越好
L o s s = − 1 N ∑ n = 1 N log 2 ( 1 + γ n N t ∥ h n H v R F , n ∥ 2 ) Loss=-\frac 1N\sum_{n=1}^N\log_2\left(1+\frac{\gamma_n}{N_t}\left\|\mathbf{h}_n^H\mathbf{v}_{RF,n} \right\|^2\right)
L o s s = − N 1 n = 1 ∑ N log 2 ( 1 + N t γ n ∥ ∥ h n H v R F , n ∥ ∥ 2 )
每一层的浮点数运算次数是( 2 N I − 1 ) N O (2N_I-1)N_O ( 2 N I − 1 ) N O N I N_I N I N O N_O N O
见BFNN中ffbn_v2.py为pytorch的实数运算版本,ffbn_test.py为测试。ffbn_complex为复数运算版本。
注意:log 2 ( A ) \log_2(A) log 2 ( A ) log ( A ) log ( 2 ) \frac{\log(A)}{\log(2)} log ( 2 ) log ( A )
新的设计方法:利用估计的CSI作为BFNN输入,直接输出最优beamforming权值。估计的信道矩阵h e s t \mathbf{h}_{\mathrm{est}} h e s t γ est \gamma_{\text {est }} γ est
新颖的Loss函数:在作者的设计中不需要标签,创新性地提出了与SE十分相关的一个Loss函数
Loss = − 1 N ∑ n = 1 N log 2 ( 1 + γ n N t ∥ h n H v R F , n ∥ 2 ) \text { Loss }=-\frac{1}{N} \sum_{n=1}^{N} \log _{2}\left(1+\frac{\gamma_{n}}{N_{\mathrm{t}}}\left\|\mathbf{h}_{n}^{H} \mathbf{v}_{\mathrm{RF}, n}\right\|^{2}\right)
Loss = − N 1 n = 1 ∑ N log 2 ( 1 + N t γ n ∥ ∥ h n H v R F , n ∥ ∥ 2 )
Loss函数的减少正好对应着平均SE的增加
对于非理性CSI的鲁棒性:提出了一种两阶段设计方法,利用估计的CSI作为输入,让BFNN学会接近理想CSI下的SE。在线部署阶段,BFNN能够适应非理性CS实现对信道估计误差的鲁棒性。
Lamda层满足恒模约束:经典的、完美的欧拉公式
v R F = exp ( j ⋅ θ ) = cos ( θ ) + j ⋅ sin ( θ ) \mathbf{v}_{\mathrm{RF}}=\exp (\mathrm{j} \cdot \boldsymbol{\theta})=\cos (\boldsymbol{\theta})+{j} \cdot \sin (\boldsymbol{\theta})
v R F = exp ( j ⋅ θ ) = cos ( θ ) + j ⋅ sin ( θ )
将相位θ \boldsymbol{\theta} θ
略
有约束!
MU-MISO
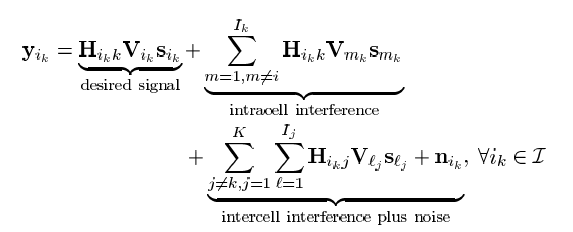
y k = h k H ∑ i = 1 K w i x i + n k y_k=\mathbf{h}_k^H\sum_{i=1}^K\mathbf{w}_ix_i+n_k
y k = h k H i = 1 ∑ K w i x i + n k
其中,h k ∈ C N × 1 \mathbf{h}_k\in \mathbb{C}^{N\times 1} h k ∈ C N × 1 x i ∼ C N ( 0 , 1 ) , n i ∼ C N ( 0 , σ 2 ) x_i\sim\mathcal{CN}(0,1),n_i\sim\mathcal{CN}(0,\sigma^2) x i ∼ C N ( 0 , 1 ) , n i ∼ C N ( 0 , σ 2 )
本文解决的问题:(P1、P2可以解得最优解,可采用监督学习;P3非凸,无最优解)
SINR balancing problem under a total power constraint,
P 1 : maximize W min 1 ≤ k ≤ K { γ k d l ρ k } , s.t. ∑ k = 1 K ∥ w k ∥ 2 ≤ P max \begin{aligned}
\mathbf{P1:}\underset{\mathbf{W}}{\operatorname{maximize}} \quad & \min_{1 \leq k \leq K}\left\{ \frac{\gamma_{k}^{d l}}{\rho_{k}}\right\}, \\
\text { s.t. } \quad&\sum_{k=1}^{K}\left\|\mathbf{w}_{k}\right\|^{2} \leq P_{\max }
\end{aligned}
P 1 : W m a x i m i z e s.t. 1 ≤ k ≤ K min { ρ k γ k d l } , k = 1 ∑ K ∥ w k ∥ 2 ≤ P max
ρ k \rho_k ρ k W = [ w 1 , w 2 , ⋯ , w K ] \mathbf{W}=[\mathbf{w_1,w_2,\cdots,w_K}] W = [ w 1 , w 2 , ⋯ , w K ] P max P_{\max} P max
power minimization problem under QoS(Quality of Service) constraints,
P 2 : min W ∑ k = 1 K ∣ ∣ w k ∣ ∣ 2 s . t . γ k d l ≥ Γ k , ∀ k . \begin{aligned}
\mathbf{P2:}\min_{\mathbf{W}} \quad& \sum_{k=1}^K||\mathbf{w}_k||^2\\
\mathrm{s.t.}\quad&\gamma_k^{dl}\ge \Gamma_k,\forall k.
\end{aligned}
P 2 : W min s . t . k = 1 ∑ K ∣ ∣ w k ∣ ∣ 2 γ k d l ≥ Γ k , ∀ k .
Γ = [ Γ 1 , ⋯ , Γ K ] T \boldsymbol{\Gamma}=[\Gamma_1,\cdots,\Gamma_K]^T Γ = [ Γ 1 , ⋯ , Γ K ] T
sum rate maximization problem under a total power constraint.
P 3 : max W ∑ k = 1 K α k log 2 ( 1 + γ k d l ) s . t . ∑ k = 1 K ∥ w k ∥ 2 ≤ P max \begin{aligned}
\mathbf{P3:}\max_{\mathbf{W}}\quad&\sum_{k=1}^K\alpha_k\log_2(1+\gamma_k^{dl})\\
\mathrm{s.t.}\quad&\sum_{k=1}^{K}\left\|\mathbf{w}_{k}\right\|^{2} \leq P_{\max }
\end{aligned}
P 3 : W max s . t . k = 1 ∑ K α k log 2 ( 1 + γ k d l ) k = 1 ∑ K ∥ w k ∥ 2 ≤ P max
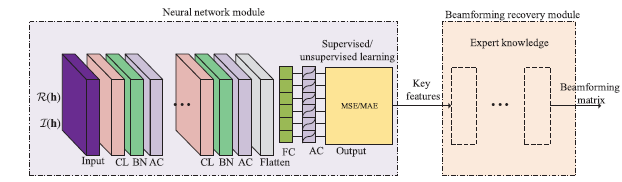
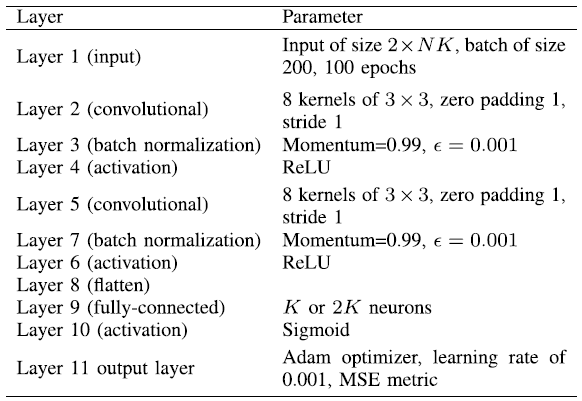
A DL-based framework for the beamforming optimization in MISO downlink, which includes two main modules: the neural network module and the beamforming recovery module . The neural network module is composed of an input layer, convolutional (CL) layers, batch normalization (BN) layers, activation (AC) layers, a flatten layer, a fully-connected (FC) layer, and an output layer, whereas the key features and the functional layers in the beamforming recovery module are specified by the expert knowledge.
输入层:h = [ h 1 H , ⋯ , h K H ] H ∈ C N K × 1 \mathbf{h}=[\mathbf{h}_1^H,\cdots,\mathbf{h}_K^H]^H\in\mathbb{C}^{NK\times1} h = [ h 1 H , ⋯ , h K H ] H ∈ C N K × 1 [ R ( h ) , I ( h ) ] T ∈ R 2 × N K [\mathfrak{R}(\mathbf{h}),\mathfrak{I}(\mathbf{h})]^T\in\mathbb{R}^{2\times NK} [ R ( h ) , I ( h ) ] T ∈ R 2 × N K
本文,BN在CONV前进行
MSE loss对异常值敏感,但数据集由仿真产生,故仍采用MSE
比起完全预测整个BF矩阵,专家知识可以有效减小需要预测的变量
通过h \mathbf{h} h q ^ \mathbf{\hat q} q ^ p ∗ \mathbf{p}^* p ∗ W ~ ∗ \mathbf{\tilde W}^* W ~ ∗ W ∗ = W ~ ∗ P ∗ \mathbf{W}^*=\mathbf{\tilde W}^*\mathbf{P}^* W ∗ = W ~ ∗ P ∗
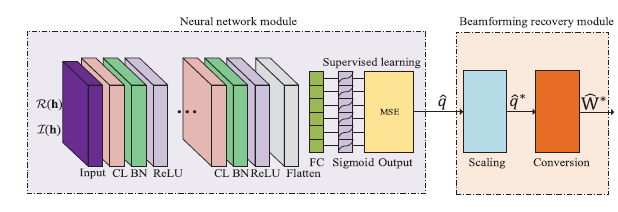
除了最后一个激活函数为Sigmoid,其它均为ReLU
Scaling——满足功率限制
q ^ ∗ = P max ∣ ∣ q ^ ∣ ∣ 1 q ^ \mathbf{\hat q}^*=\frac{P_{\max}}{||\mathbf{\hat q}||_1}\mathbf{\hat q}
q ^ ∗ = ∣ ∣ q ^ ∣ ∣ 1 P max q ^
conversion——由q ^ ∗ \mathbf{\hat q}^* q ^ ∗ W ^ ∗ \mathbf{\hat W}^* W ^ ∗
Loss函数采用MSE度量
同样,通过h \mathbf{h} h q ^ \mathbf{\hat q} q ^ p ∗ \mathbf{p}^* p ∗ W ~ ∗ \mathbf{\tilde W}^* W ~ ∗ W ∗ = W ~ ∗ P ∗ \mathbf{W}^*=\mathbf{\tilde W}^*\mathbf{P}^* W ∗ = W ~ ∗ P ∗ 但无功率约束,不需要上行链路power allocation矢量归一化。
conversion
与P1不同,当q ^ ∗ \mathbf{\hat q}^* q ^ ∗ q ∗ \mathbf{q}^* q ∗ p ^ ∗ \mathbf{\hat p}^* p ^ ∗
Sum-rate优化问题没有最优解。
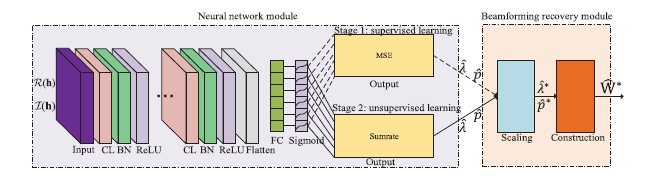
第一阶段 先通过监督学习逼近传统WMMSE算法的局部最优解,称为“预训练”
L o s s = 1 2 L K ∑ l = 1 L ( ∥ p ‾ ( l ) − p ^ ( l ) ∥ 2 2 + ∥ λ ‾ ( l ) − λ ^ ( l ) ∥ 2 2 ) Loss=\frac{1}{2LK}\sum_{l=1}^L\left(\left\|\mathbf{\underline p}^{(l)}-\mathbf{\hat p}^{(l)}\right\|_2^2+\left\|\boldsymbol{\underline \lambda}^{(l)}-\boldsymbol{\hat \lambda}^{(l)}\right\|_2^2\right)
L o s s = 2 L K 1 l = 1 ∑ L ( ∥ ∥ ∥ p ( l ) − p ^ ( l ) ∥ ∥ ∥ 2 2 + ∥ ∥ ∥ λ ( l ) − λ ^ ( l ) ∥ ∥ ∥ 2 2 )
其中,p \mathbf{p} p λ \boldsymbol{\lambda} λ
第二阶段 直接计算这个算法的优化目标函数作为loss,进行无监督学习。
Loss = − 1 2 K L ∑ l = 1 L ∑ k = 1 K α k ( l ) log 2 ( 1 + γ k u l , ( l ) ) ⏟ s u m − r a t e \text { Loss }=-\frac{1}{2 K L} \sum_{l=1}^{L} \underbrace{\sum_{k=1}^{K} \alpha_{k}^{(l)} \log _{2}\left(1+\gamma_{k}^{u l,(l)}\right)}_{sum-rate}
Loss = − 2 K L 1 l = 1 ∑ L s u m − r a t e k = 1 ∑ K α k ( l ) log 2 ( 1 + γ k u l , ( l ) )
分两个阶段的作用:显著增强学习效果,加快收敛。(杨神:?)
scaling——满足功率约束,2 K 2K 2 K
p ^ ∗ = P max ∣ ∣ p ^ ∣ ∣ 1 p ^ and λ ^ ∗ = P max ∣ ∣ λ ^ ∣ ∣ 1 λ ^ \mathbf{\hat p}^*=\frac{P_{\max}}{||\mathbf{\hat p}||_1}\mathbf{\hat p}\quad\text{and}\quad\boldsymbol{\hat \lambda}^*=\frac{P_{\max}}{||\boldsymbol{\hat \lambda}||_1}\boldsymbol{\hat \lambda}
p ^ ∗ = ∣ ∣ p ^ ∣ ∣ 1 P max p ^ and λ ^ ∗ = ∣ ∣ λ ^ ∣ ∣ 1 P max λ ^
construction——P max P_{\max} P max ∑ k = 1 K λ i = P max \sum_{k=1}^K\lambda_i=P_{\max} ∑ k = 1 K λ i = P max
w ^ k ∗ = p ^ k ∗ ( I N + ∑ k = 1 K λ ^ k ∗ σ 2 h k h k H ) − 1 h k ∥ ( I N + ∑ k = 1 K λ ^ k ∗ σ 2 h k h k H ) − 1 h k ∥ 2 , ∀ k \hat{\mathbf{w}}_{k}^{*}=\sqrt{\hat{p}_{k}^{*}} \frac{\left(\mathbf{I}_{N}+\sum_{k=1}^{K} \frac{\hat{\lambda}_{k}^{*}}{\sigma^{2}} \mathbf{h}_{k} \mathbf{h}_{k}^{H}\right)^{-1} \mathbf{h}_{k}}{\left\|\left(\mathbf{I}_{N}+\sum_{k=1}^{K} \frac{\hat{\lambda}_{k}^{*}}{\sigma^{2}} \mathbf{h}_{k} \mathbf{h}_{k}^{H}\right)^{-1} \mathbf{h}_{k}\right\|_{2}}, \quad \forall k
w ^ k ∗ = p ^ k ∗ ∥ ∥ ∥ ∥ ( I N + ∑ k = 1 K σ 2 λ ^ k ∗ h k h k H ) − 1 h k ∥ ∥ ∥ ∥ 2 ( I N + ∑ k = 1 K σ 2 λ ^ k ∗ h k h k H ) − 1 h k , ∀ k
所提出的框架利用了专家知识,如上行链路和下行链路的二元性以及已知的最佳解决方案的结构。这种知识通过允许人们指定要学习的最佳参数来提高精简效率;这些参数通常不是波束成形矩阵条目。
略
三类DL处理的问题:
One of the areas of interest is to deal with scenarios in which the channel
Another area of interest is to optimize the end-to-end system performance,对端到端系统的优化
The third area of interest is to overcome the complexity of wireless networks,无线网络的复杂度问题
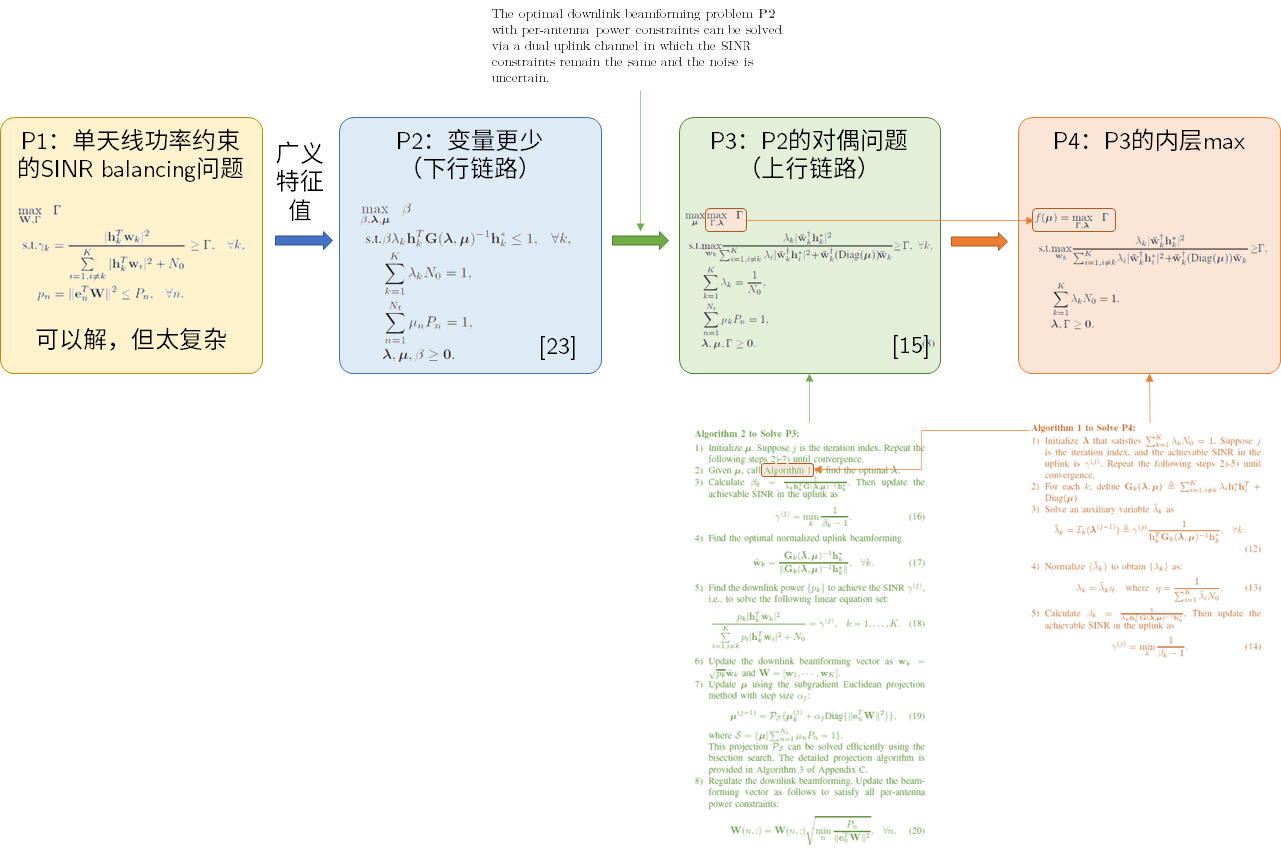
在上一篇文章的基础上增加了单天线约束(过去大部分文章讨论MU-MISO,即基站多天线用户单天线问题)
在基站侧单天线功率约束下,最大化最小接收信干噪比或平衡信干噪比
——独立的非频选瑞利快衰落
波束赋形矩阵:W = [ w 1 , w 2 , ⋯ , w K ] ∈ C N t × K \mathbf{W}=[\mathbf{w_1,w_2,\cdots,w_K}]\in\mathbb{C}^{N_t\times K} W = [ w 1 , w 2 , ⋯ , w K ] ∈ C N t × K
p n = ∥ W ( n , : ) ∥ 2 = ∥ e n W ∥ 2 p_n=\left\|\mathbf{W}(n,:) \right\|^2=\left\|\mathbf{e}_n\mathbf{W} \right\|^2
p n = ∥ W ( n , : ) ∥ 2 = ∥ e n W ∥ 2
其中,e n \mathbf{e}_n e n n n n
P1: max W , Γ Γ s.t. γ k = ∣ h k T w k ∣ 2 ∑ i = 1 , i ≠ k K ∣ h k T w i ∣ 2 + N 0 ≥ Γ , ∀ k , p n = ∥ e n T W ∥ 2 ≤ P n , ∀ n . \begin{aligned}
\textbf { P1: } \max _{\mathbf{W}, \Gamma} \quad &\Gamma \\
\text { s.t. }\quad& \gamma_{k} =\frac{\left|\mathbf{h}_{k}^{T} \mathbf{w}_{k}\right|^{2}}{\sum_{i=1, i \neq k}^{K}\left|\mathbf{h}_{k}^{T} \mathbf{w}_{i}\right|^{2}+N_{0}} \geq \Gamma, \quad \forall k, \\
& p_{n} =\left\|\mathbf{e}_{n}^{T} \mathbf{W}\right\|^{2} \leq P_{n}, \quad \forall n .
\end{aligned}
P1: W , Γ max s.t. Γ γ k = ∑ i = 1 , i = k K ∣ ∣ h k T w i ∣ ∣ 2 + N 0 ∣ ∣ h k T w k ∣ ∣ 2 ≥ Γ , ∀ k , p n = ∥ ∥ e n T W ∥ ∥ 2 ≤ P n , ∀ n .
通过广义特征值算法,可以转化为问题P2
P 2 : max β , λ , μ β s.t. β λ k h k T G ( λ , μ ) − 1 h k ∗ ≤ 1 , ∀ k , ∑ k = 1 K λ k N 0 = 1 , ∑ n = 1 N t μ n P n = 1 , λ , μ , β ≥ 0. \begin{aligned}
\mathbf{P 2}: \max _{\beta, \boldsymbol{\lambda}, \boldsymbol{\mu}}\quad & \beta \\
\text { s.t. } \quad&\beta \lambda_{k} \mathbf{h}_{k}^{T} \mathbf{G}(\boldsymbol{\lambda}, \boldsymbol{\mu})^{-1} \mathbf{h}_{k}^{*} \leq 1, \quad \forall k, \\
& \sum_{k=1}^{K} \lambda_{k} N_{0}=1, \\
& \sum_{n=1}^{N_{t}} \mu_{n} P_{n}=1, \\
& \boldsymbol{\lambda}, \boldsymbol{\mu}, \beta \geq \mathbf{0} .
\end{aligned}
P 2 : β , λ , μ max s.t. β β λ k h k T G ( λ , μ ) − 1 h k ∗ ≤ 1 , ∀ k , k = 1 ∑ K λ k N 0 = 1 , n = 1 ∑ N t μ n P n = 1 , λ , μ , β ≥ 0 .
其中,G ( λ , μ ) ≜ ∑ i = 1 K λ i h i ∗ h i T + d i a g ( μ ) \mathbf{G}(\boldsymbol{\lambda}, \boldsymbol{\mu})\triangleq\sum_{i=1}^K\lambda_i\mathbf{h}_i^*\mathbf{h}_i^T+diag(\boldsymbol{\mu}) G ( λ , μ ) ≜ ∑ i = 1 K λ i h i ∗ h i T + d i a g ( μ )
λ ∈ Z K \boldsymbol{\lambda}\in\mathbb{Z}^K λ ∈ Z K μ ∈ Z N t \boldsymbol{\mu}\in\mathbb{Z}^{N_t} μ ∈ Z N t
β = 1 + 1 Γ \beta=1+\frac{1}{\Gamma} β = 1 + Γ 1
The optimal downlink beamforming problem P2 with per-antenna power constraints can be solved via a dual uplink channel in which the SINR constraints remain the same and the noise is uncertain. 通过对偶性转化成上行链路问题P3max μ max Γ , λ Γ \max_{\boldsymbol{\mu}}\max_{\Gamma,\boldsymbol{\lambda}} \Gamma max μ max Γ , λ Γ u \mathbf{u} u f ( u ) = max Γ , λ Γ f(\mathbf{u})=\max_{\Gamma,\boldsymbol{\lambda}} \Gamma f ( u ) = max Γ , λ Γ μ \boldsymbol{\mu} μ
two strategies:
one is to learn the dual variables μ λ
the other is to learn only the dual variable μ μ \boldsymbol{\mu} μ λ \boldsymbol{\lambda} λ
DL结构的一般性:由于用户数量K K K N t N_t N t
Transfer learning——【ai3-52】
training set augmentation(训练集扩大)——训练集中样本的N t , K N_t,K N t , K 2 × N t ′ K ′ 2\times N_t'K' 2 × N t ′ K ′ K ′ K' K ′ N t ′ > N t , K ′ > K N_t'>N_t,K'>K N t ′ > N t , K ′ > K
本文提出的和优化算法针对信道估计误差是鲁棒的。
当N t ≥ K N_t\geq K N t ≥ K
提出了subgradient算法,收敛更快
提出了学习双变量的DL框架
开发了一种启发式算法,通过数据augmentation适应不同的用户数和天线数,提高泛化能力(?)
testbed实验
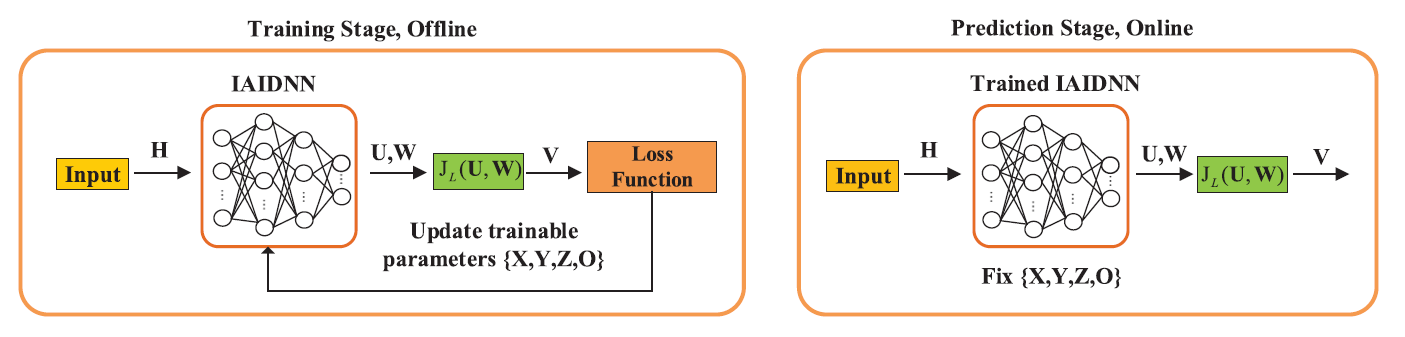
Iterative Algorithm Induced Deep-Unfolding Neural Networks: Precoding Design for Multiuser MIMO Systems
本文部分链接和引用没法用,链接的是预编码论文阅读(一)中迭代的那篇文章“An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel ”
建模同文章“An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel ”
优化问题(目标函数):
min X E Z { f ( X ; θ , Z ) } , s.t. X ∈ X \min_\mathbf{X}\quad \mathbb{E}_\mathbf{Z}\{f(\mathbf{X};\boldsymbol{\theta},\mathbf{Z})\},\quad\text{s.t.}\ \mathbf{X}\in\mathcal{X}
X min E Z { f ( X ; θ , Z ) } , s.t. X ∈ X
其中,θ \boldsymbol{\theta} θ X \mathbf{X} X Z \mathbf{Z} Z
前向传播:
X l = F l ( X l − 1 ; θ , Z ) \mathbf{X}^l=\mathcal{F}_l(\mathbf{X}^{l-1};\boldsymbol{\theta},\mathbf{Z})
X l = F l ( X l − 1 ; θ , Z )
在本文中,前向传播的模型为
X l = A ˉ X l − 1 B ˉ X l − 1 C ˉ + φ ( A ˉ X l − 1 B ˉ X l − 1 C ˉ ) D ˉ \mathbf{X}^l=\bar{\mathbf{A}}\mathbf{X}^{l-1}\bar{\mathbf{B}}\mathbf{X}^{l-1}\bar{\mathbf{C}}+\varphi(\bar{\mathbf{A}}\mathbf{X}^{l-1}\bar{\mathbf{B}}\mathbf{X}^{l-1}\bar{\mathbf{C}})\bar{\mathbf{D}}
X l = A ˉ X l − 1 B ˉ X l − 1 C ˉ + φ ( A ˉ X l − 1 B ˉ X l − 1 C ˉ ) D ˉ
反向传播:GCR in Matrix Form(更一般的链式法则)
Tr { G l d X l } = ( 5 ) Tr { ( B ‾ X l − 1 C ‾ G l ( D ‾ ∘ φ ′ ( A ‾ X l − 1 B ‾ X l − 1 C ‾ ) T + I ) A ‾ + C ‾ G l ( D ‾ ∘ φ ′ ( A ‾ X l − 1 B ‾ X l − 1 C ‾ ) T + I ) A ‾ X l − 1 B ‾ ) d X l − 1 } \begin{aligned}
&\operatorname{Tr}\left\{\mathbf{G}^{l} d \mathbf{X}^{l}\right\} \\
&\stackrel{(5)}{=} \operatorname{Tr}\left\{\left(\overline{\mathbf{B}} \mathbf{X}^{l-1} \overline{\mathbf{C}} \mathbf{G}^{l}\left(\overline{\mathbf{D}} \circ \varphi^{\prime}\left(\overline{\mathbf{A}} \mathbf{X}^{l-1} \overline{\mathbf{B}} \mathbf{X}^{l-1} \overline{\mathbf{C}}\right)^{T}+\mathbf{I}\right) \overline{\mathbf{A}}\right.\right. \\
&\left.\left.\quad+\overline{\mathbf{C}} \mathbf{G}^{l}\left(\overline{\mathbf{D}} \circ \varphi^{\prime}\left(\overline{\mathbf{A}} \mathbf{X}^{l-1} \overline{\mathbf{B}} \mathbf{X}^{l-1} \overline{\mathbf{C}}\right)^{T}+\mathbf{I}\right) \overline{\mathbf{A}} \mathbf{X}^{l-1} \overline{\mathbf{B}}\right) d \mathbf{X}^{l-1}\right\}
\end{aligned}
T r { G l d X l } = ( 5 ) T r { ( B X l − 1 C G l ( D ∘ φ ′ ( A X l − 1 B X l − 1 C ) T + I ) A + C G l ( D ∘ φ ′ ( A X l − 1 B X l − 1 C ) T + I ) A X l − 1 B ) d X l − 1 }
G l \mathbf{G}^l G l X l \mathbf{X}^l X l ∘ \circ ∘
**该网络的创新点:**In comparison with applying the platforms such as “Pytorch” and “Tensorflow” to do the BP, the GCR has three advantages
The platforms cannot do BP for the complex trainable parameters;
There are some operations these platforms cannot do, such as the inversion and the determinant of a complex matrix;
Based on the GCR, the closed-form gradients are obtained, which is more accurate and provides faster convergence speed compared with the automatic differential of the platforms.
Then, based on the GCR presented in Theorem 1, the gradient in each layer, i.e., { G l , l ∈ L } \{\mathbf{G}^l,l\in\mathcal{L}\} { G l , l ∈ L } θ l \boldsymbol{\theta}^l θ l G l \mathbf{G}^l G l
将功率限制,考虑到\eqref{eq:2-1}的目标函数中,考虑无约束的SR问题(13)
max { V k } ∑ k = 1 K ω k log det ( I + H k V k V k H H k H ( ∑ m ≠ k H k V m V m H H k H + σ k 2 P T ∑ n = 1 K Tr ( V n V n H ) I ) − 1 ) \begin{aligned}
\max _{\left\{\mathbf{V}_{k}\right\}} \quad& \sum_{k=1}^{K} \omega_{k} \log \operatorname{det}\left(\mathbf{I}+\mathbf{H}_{k} \mathbf{V}_{k} \mathbf{V}_{k}^{H} \mathbf{H}_{k}^{H}\right.\\
&\left.\left(\sum_{m \neq k} \mathbf{H}_{k} \mathbf{V}_{m} \mathbf{V}_{m}^{H} \mathbf{H}_{k}^{H}+\frac{\sigma_{k}^{2}}{P_{T}} \sum_{n=1}^{K} \operatorname{Tr}\left(\mathbf{V}_{n} \mathbf{V}_{n}^{H}\right) \mathbf{I}\right)^{-1}\right)
\end{aligned}
{ V k } max k = 1 ∑ K ω k log d e t ( I + H k V k V k H H k H ⎝ ⎛ m = k ∑ H k V m V m H H k H + P T σ k 2 n = 1 ∑ K T r ( V n V n H ) I ⎠ ⎞ − 1 ⎠ ⎟ ⎞
式\eqref{eq:ai4-13}的最优解V ⋆ ⋆ \mathbf{V}^{\star\star} V ⋆ ⋆ V ⋆ \mathbf{V}^{\star} V ⋆
V k ⋆ = α V k ⋆ ⋆ , α = P T ( ∑ k = 1 K T r ( V k ⋆ ⋆ ( V k ⋆ ⋆ ) H ) ) 1 2 \mathbf{V}_k^{\star}=\alpha\mathbf{V}_k^{\star\star},\quad\alpha=\frac{\sqrt{P_T}}{\left(\sum_{k=1}^K Tr(\mathbf{V}_k^{\star\star}(\mathbf{V}_k^{\star\star})^H) \right)^{\frac12}}
V k ⋆ = α V k ⋆ ⋆ , α = ( ∑ k = 1 K T r ( V k ⋆ ⋆ ( V k ⋆ ⋆ ) H ) ) 2 1 P T
进一步考虑,MMSE问题和WSR问题的同一性,将问题就转换成了无约束的MMSE问题
min { W k , U k , V k } ∑ k = 1 K ω k ( Tr ( W k E 2 , k ) − log det ( W k ) ) \min _{\left\{\mathbf{W}_{k}, \mathbf{U}_{k}, \mathbf{V}_{k}\right\}} \sum_{k=1}^{K} \omega_{k}\left(\operatorname{Tr}\left(\mathbf{W}_{k} \mathbf{E}_{2, k}\right)-\log \operatorname{det}\left(\mathbf{W}_{k}\right)\right)
{ W k , U k , V k } min k = 1 ∑ K ω k ( T r ( W k E 2 , k ) − log d e t ( W k ) )
其中,
E 2 , k ≜ ( I − U k H H k V k ) ( I − U k H H k V k ) H + ∑ m ≠ k U k H H k V m V m H H k H U k + ∑ n = 1 K Tr ( V n V n H ) P T σ k 2 U k H U k \begin{aligned}
&\mathbf{E}_{2, k} \triangleq\left(\mathbf{I}-\mathbf{U}_{k}^{H} \mathbf{H}_{k} \mathbf{V}_{k}\right)\left(\mathbf{I}-\mathbf{U}_{k}^{H} \mathbf{H}_{k} \mathbf{V}_{k}\right)^{H} \\
&+\sum_{m \neq k} \mathbf{U}_{k}^{H} \mathbf{H}_{k} \mathbf{V}_{m} \mathbf{V}_{m}^{H} \mathbf{H}_{k}^{H} \mathbf{U}_{k}+\frac{\sum_{n=1}^{K} \operatorname{Tr}\left(\mathbf{V}_{n} \mathbf{V}_{n}^{H}\right)}{P_{T}} \sigma_{k}^{2} \mathbf{U}_{k}^{H} \mathbf{U}_{k}
\end{aligned}
E 2 , k ≜ ( I − U k H H k V k ) ( I − U k H H k V k ) H + m = k ∑ U k H H k V m V m H H k H U k + P T ∑ n = 1 K T r ( V n V n H ) σ k 2 U k H U k
算法流程图:
与上述分析的深度展开网络中参数的对照:
X ≡ { W k , U k , V k , ∀ k ∈ K } Z ≡ { H k , ω k , σ k , P T , ∀ k ∈ K } \begin{aligned}
\mathbf{X}\equiv&\left\{\mathbf{W}_k,\mathbf{U}_k,\mathbf{V}_k,\forall k\in\mathcal{K} \right\}\\
\mathbf{Z}\equiv&\left\{\mathbf{H}_k,\omega_k,\sigma_k,P_T,\forall k\in\mathcal{K} \right\}
\end{aligned}
X ≡ Z ≡ { W k , U k , V k , ∀ k ∈ K } { H k , ω k , σ k , P T , ∀ k ∈ K }
迭代过程:
U t = F t ( V t − 1 ) W t = G t ( U t , V t − 1 ) V t = J t ( U t , W t ) \begin{aligned}
\mathbf{U}^t=&F_t(\mathbf{V}^{t-1})\\
\mathbf{W}^t=&G_t(\mathbf{U}^t,\mathbf{V}^{t-1})\\
\mathbf{V}^t=&J_t(\mathbf{U}^t,\mathbf{W}^t)
\end{aligned}
U t = W t = V t = F t ( V t − 1 ) G t ( U t , V t − 1 ) J t ( U t , W t )
减小矩阵求逆的计算量的两种途径
用A + = ( A ∘ I ) − 1 \mathbf{A}^+=(\mathbf{A}\circ\mathbf{I})^{-1} A + = ( A ∘ I ) − 1 A − 1 \mathbf{A}^{-1} A − 1 A + X \mathbf{A^+X} A + X X \mathbf{X} X
用A − 1 \mathbf{A}^{-1} A − 1 2 A 0 − 1 − A 0 − 1 A A 0 − 1 2\mathbf{A}_0^{-1}-\mathbf{A}_0^{-1}\mathbf{AA}_0^{-1} 2 A 0 − 1 − A 0 − 1 A A 0 − 1 A Y + Z \mathbf{AY+Z} A Y + Z Y , Z \mathbf{Y,Z} Y , Z
【?】用A + X + A Y + Z \mathbf{A^+X+AY+Z} A + X + A Y + Z A − 1 \mathbf{A}^{-1} A − 1
迭代算法中U , W , V \mathbf{U,W,V} U , W , V U , V \mathbf{U,V} U , V { O k u , l + 1 , O k v , l + 1 } \left\{\mathbf{O}_k^{u,l+1},\mathbf{O}_k^{v,l+1} \right\} { O k u , l + 1 , O k v , l + 1 }
V \mathbf{V} V U , W \mathbf{U,W} U , W U , W \mathbf{U,W} U , W V \mathbf{V} V U , W \mathbf{U,W} U , W Loss函数:
max { V k } ∑ k = 1 K E H k { ω k log det ( I + H k V k V k H H k H ( ∑ m ≠ k H k V m V m H H k H + σ k 2 P T ∑ k Tr ( V k V k H ) I ) − 1 ) } \max _{\left\{\mathbf{V}_{k}\right\}} \sum_{k=1}^{K} \mathbb{E}_{\mathbf{H}_{k}}\left\{\omega_{k} \log \operatorname{det}\left(\mathbf{I}+\mathbf{H}_{k} \mathbf{V}_{k} \mathbf{V}_{k}^{H} \mathbf{H}_{k}^{H}\left(\sum_{m \neq k} \mathbf{H}_{k} \mathbf{V}_{m} \mathbf{V}_{m}^{H} \mathbf{H}_{k}^{H}+\frac{\sigma_{k}^{2}}{P_{T}} \sum_{k} \operatorname{Tr}\left(\mathbf{V}_{k} \mathbf{V}_{k}^{H}\right) \mathbf{I}\right)^{-1}\right)\right\}
{ V k } max k = 1 ∑ K E H k ⎩ ⎪ ⎨ ⎪ ⎧ ω k log d e t ⎝ ⎜ ⎛ I + H k V k V k H H k H ⎝ ⎛ m = k ∑ H k V m V m H H k H + P T σ k 2 k ∑ T r ( V k V k H ) I ⎠ ⎞ − 1 ⎠ ⎟ ⎞ ⎭ ⎪ ⎬ ⎪ ⎫
反向传播不直接对训练参数进行计算,而先对中间的迭代变量进行计算!
对迭代变量U , W , V \mathbf{U,W,V} U , W , V
最后一层由目标函数代入V k L \mathbf{V}_k^L V k L U k L , W k L \mathbf{U_k^L,W_k^L} U k L , W k L G k u , L , G k v , L \mathbf{G_k^{u,L}},\mathbf{G_k^{v,L}} G k u , L , G k v , L
中间层由GCR算法,从l + 1 l+1 l + 1 U , W , V \mathbf{U,W,V} U , W , V l l l
进一步通过链式法则求解出训练参数的梯度
采取梯度下降方法训练网络
初始值的选定:训练参数随机初始化;V k 0 \mathbf{V}^0_k V k 0
类似【ai2】,
输入:H ≜ [ H 1 T , H 2 T , ⋯ , H k T ] T \mathbf{H}\triangleq [\mathbf H_1^T,\mathbf H_2^T,\cdots,\mathbf H_k^T]^T H ≜ [ H 1 T , H 2 T , ⋯ , H k T ] T
输出:U k , W k \mathbf{U_k,W_k} U k , W k
流程:
监督:先逼近传统的WMMSE,用求U , W \mathbf{U,W} U , W
无监督:再用代入V k \mathbf V_k V k
参数
IAIDNN的参数维度取决于需要训练的参数{ X k u , l , Y k u , l , Z k u , l , O k u , l } \left\{\mathbf X_k^{u,l},\mathbf Y_k^{u,l},\mathbf Z_k^{u,l},\mathbf O_k^{u,l}\right\} { X k u , l , Y k u , l , Z k u , l , O k u , l } { X k w , l , Y k w , l , Z k w , l } \left\{\mathbf X_k^{w,l},\mathbf Y_k^{w,l},\mathbf Z_k^{w,l}\right\} { X k w , l , Y k w , l , Z k w , l } { X k v , l , Y k v , l , Z k v , l , O k v , l } \left\{\mathbf X_k^{v,l},\mathbf Y_k^{v,l},\mathbf Z_k^{v,l},\mathbf O_k^{v,l}\right\} { X k v , l , Y k v , l , Z k v , l , O k v , l } V \mathbf V V
普通中间层: ( 3 N r 2 + 3 d 2 + 3 N t 2 + d N r + d N t ) K 最后一层: L K ( 3 N r 2 + 3 d 2 + d N r ) + ( L − 1 ) K ( 3 N t 2 + d N t ) \begin{aligned}
\text{普通中间层:}&\left(3 N_{r}^{2}+3 d^{2}+3 N_{t}^{2}+d N_{r}+d N_{t}\right) K\\
\text{最后一层:}&L K\left(3 N_{r}^{2}+3 d^{2}+d N_{r}\right)+(L-1) K\left(3 N_{t}^{2}+d N_{t}\right)
\end{aligned}
普通中间层: 最后一层: ( 3 N r 2 + 3 d 2 + 3 N t 2 + d N r + d N t ) K L K ( 3 N r 2 + 3 d 2 + d N r ) + ( L − 1 ) K ( 3 N t 2 + d N t )
CNN
∑ l = 1 L − 2 S l 2 C l − 1 C l + K N r N t C L − 2 C out \sum_{l=1}^{L-2} S_{l}^{2} C_{l-1} C_{l}+K N_{r} N_{t} C_{L-2} C_{\text {out }}
l = 1 ∑ L − 2 S l 2 C l − 1 C l + K N r N t C L − 2 C out
卷积核S l = 5 S_l=5 S l = 5 C l = 32 C_l=32 C l = 3 2 C o u t = 1024 C_{out}=1024 C o u t = 1 0 2 4
复杂度
传统WMMSE需要迭代L W L_W L W L a L_a L a L a ≪ L w L_a\ll L_w L a ≪ L w
相比传统的矩阵求逆需要O ( n 3 ) \mathcal{O}(n^3) O ( n 3 ) O ( n 2.37 ) \mathcal{O}(n^{2.37}) O ( n 2 . 3 7 )
IAIDNN的闭式梯度比传统黑箱CNN训练时间更短、效果更好
泛化能力
同【ai3】可以训练( N t 0 , N r 0 , K 0 ) (N_{t0},N_{r0},K_0) ( N t 0 , N r 0 , K 0 ) ( N t 1 , N r 1 , K 1 ) (N_{t1},N_{r1},K_1) ( N t 1 , N r 1 , K 1 ) ( N t 1 < N t 0 , N r 1 < N t 0 , K 1 < K 0 ) (N_{t1}<N_{t0},N_{r1}<N_{t0},K_1<K_{0}) ( N t 1 < N t 0 , N r 1 < N t 0 , K 1 < K 0 )
同【ai1】可以训练在不同P T , σ k P_T,\sigma_k P T , σ k V \mathbf V V
We propose a framework for deep-unfolding, where the general form of IAIDNN is developed in matrix form to better solve the problems in communication systems. To train the IAIDNN, the GCR is proposed to calculate the gradients of the trainable parameters.
We implement the proposed deep-unfolding framework to solve the sum-rate maximization problem for precoding design in MU-MIMO systems. Based on the structure of the iterative WMMSE algorithm, an efficient IAIDNN is developed, where the iterative WMMSE algorithm is unfolded into a layer-wise structure.
We analyze the computational complexity and generalization ability of the proposed schemes. Simulation results show that the proposed IAIDNN efficiently achieves the performance of the iterative WMMSE algorithm with reduced computational complexity. The contribution becomes more significant in a massive MU-MIMO system.
model-driven
反向传播——矩阵形式的广义链式法则
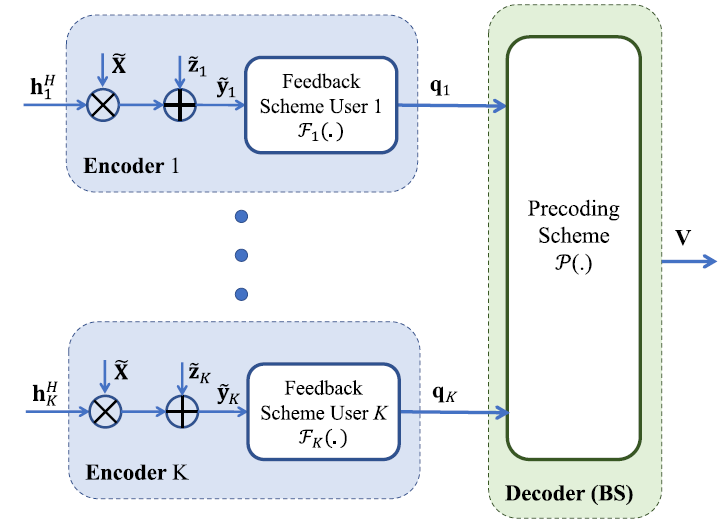
Deep Learning for Distributed Channel Feedback and Multiuser Precoding in FDD Massive MIMO ——imperfect CSI
MU-MISO
maximize X ~ , { F k ( ⋅ ) } ∀ k , P ( ⋅ ) ∑ k = 1 K log 2 ( 1 + ∣ h k H v k ∣ 2 ∑ j ≠ k ∣ h k H v j ∣ 2 + σ 2 ) subject to V = P ( [ q 1 T , … , q K T ] T ) q k = F k ( h k H X ~ + z ~ k ) , ∀ k Tr ( V V H ) ≤ P ∥ x ~ ℓ ∥ 2 2 ≤ P , ∀ ℓ \begin{aligned}
\underset{\tilde{\mathbf{X}},\left\{\mathcal{F}_{k}(\cdot)\right\}_{\forall k}, \mathcal{P}(\cdot)}{\operatorname{maximize}} \quad & \sum_{k=1}^{K} \log _{2}\left(1+\frac{\left|\mathbf{h}_{k}^{H} \mathbf{v}_{k}\right|^{2}}{\sum_{j \neq k}\left|\mathbf{h}_{k}^{H} \mathbf{v}_{j}\right|^{2}+\sigma^{2}}\right) \\
\text { subject to } \quad & \mathbf{V}=\mathcal{P}\left(\left[\mathbf{q}_{1}^{T}, \ldots, \mathbf{q}_{K}^{T}\right]^{T}\right) \\
& \mathbf{q}_{k}=\mathcal{F}_{k}\left(\mathbf{h}_{k}^{H} \widetilde{\mathbf{X}}+\widetilde{\mathbf{z}}_{k}\right), \quad \forall k \\
& \operatorname{Tr}\left(\mathbf{V} \mathbf{V}^{H}\right) \leq P \\
&\left\|\widetilde{\mathbf{x}}_{\ell}\right\|_{2}^{2} \leq P, \quad \forall \ell
\end{aligned}
X ~ , { F k ( ⋅ ) } ∀ k , P ( ⋅ ) m a x i m i z e subject to k = 1 ∑ K log 2 ( 1 + ∑ j = k ∣ ∣ h k H v j ∣ ∣ 2 + σ 2 ∣ ∣ h k H v k ∣ ∣ 2 ) V = P ( [ q 1 T , … , q K T ] T ) q k = F k ( h k H X + z k ) , ∀ k T r ( V V H ) ≤ P ∥ x ℓ ∥ 2 2 ≤ P , ∀ ℓ
其中,X ~ \tilde{\mathbf{X}} X ~ F k : C 1 × L → { ± 1 } B \mathcal{F}_k:\mathbb{C}^{1\times L}\to \{\pm 1\}^B F k : C 1 × L → { ± 1 } B k k k q k \mathbf{q}_k q k B B B P : { ± 1 } K B → C M × K \mathcal{P}:\{\pm 1\}^{KB}\to \mathbb{C}^{M\times K} P : { ± 1 } K B → C M × K
分布式信源编码
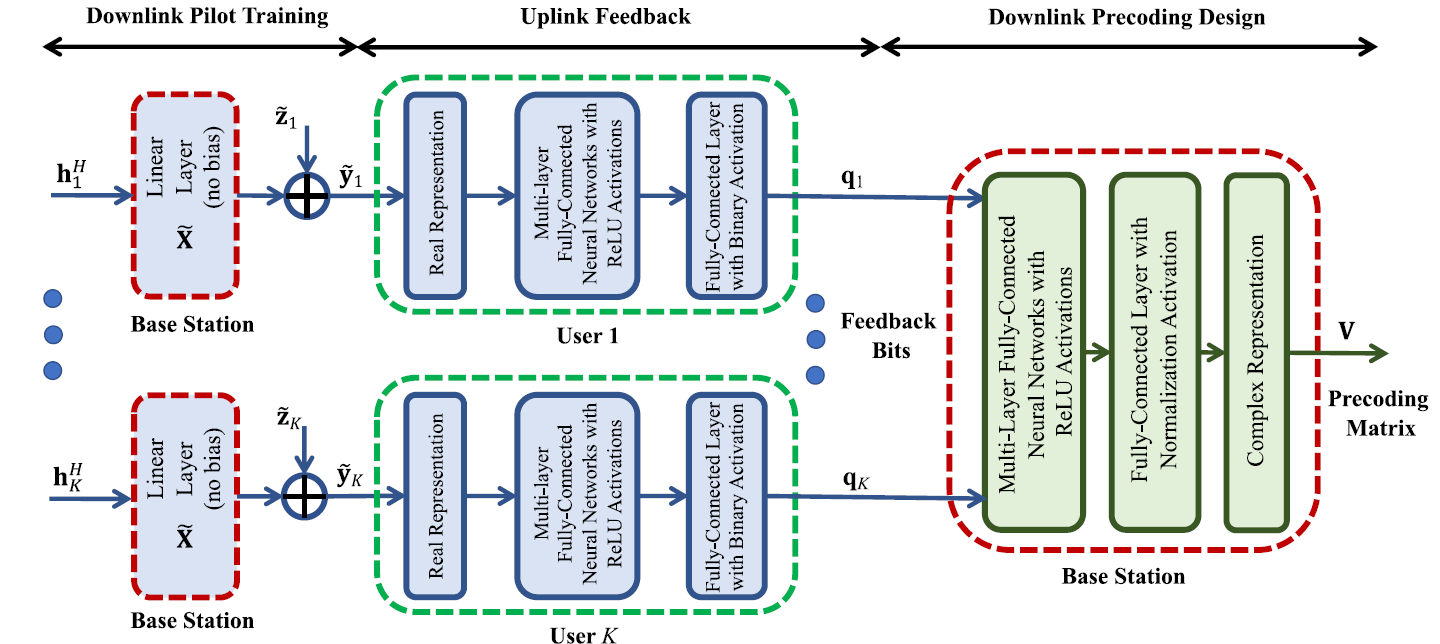
downlink training and uplink feedback phase
downlink data transmission phase
Downlink Pilot Training:训练参数X ~ \widetilde{\mathbf X} X
作为全连接层,训练导频X ~ \tilde{\mathbf{X}} X ~ σ 2 \sigma^2 σ 2
Uplink Feedback:(用户侧)参数Θ R ( k ) = { W r ( k ) , b r ( k ) } r = 1 R \Theta_\text{R}^{(k)}=\left\{\mathbf W_r^{(k)},\mathbf b_r^{(k)} \right\}_{r=1}^R Θ R ( k ) = { W r ( k ) , b r ( k ) } r = 1 R
输入:
y ˉ k ≜ [ ℜ ( y ~ k ) , I ( y ~ k ) ] \bar{\mathbf y}_k\triangleq[\Re{(\tilde{\mathbf y}_k)},\mathcal{I} (\tilde{\mathbf y}_k)]
y ˉ k ≜ [ ℜ ( y ~ k ) , I ( y ~ k ) ]
中间层采用ReLU,最后一层用符号函数
q k = s g n ( W R ( k ) σ R − 1 ( ⋯ σ 1 ( W 1 y ˉ k + b 1 ( k ) ) ⋯ ) + b R ( k ) ) \mathbf{q}_k=sgn\left(\mathbf W_R^{(k)}\sigma_{R-1}\left(\cdots\sigma_1\left(\mathbf W_1\bar{\mathbf y}_k+\mathbf b_1^{(k)}\right)\cdots\right)+\mathbf b_R^{(k)}\right)
q k = s g n ( W R ( k ) σ R − 1 ( ⋯ σ 1 ( W 1 y ˉ k + b 1 ( k ) ) ⋯ ) + b R ( k ) )
Downlink Precoding Design: (BS侧)参数Θ T = { W t , b t } t = 1 T \Theta_\text{T}=\left\{\mathbf W_t,\mathbf b_t \right\}_{t=1}^T Θ T = { W t , b t } t = 1 T
输出:
v = [ v e c ( ℜ ( V ) ) T , v e c ( I ( V ) ) T ] T \mathbf v=\left[vec(\Re{(\mathbf V)})^T,vec(\mathcal{I} (\mathbf V))^T\right]T
v = [ v e c ( ℜ ( V ) ) T , v e c ( I ( V ) ) T ] T
中间层采用ReLU,最后一层则需要功率约束,对功率进行归一化σ ~ T ( ∙ ) = P ∙ ∥ ∙ ∥ 2 \tilde\sigma_T(\bullet)=\sqrt{P}\frac{\bullet}{\left\|\bullet\right\|_2} σ ~ T ( ∙ ) = P ∥ ∙ ∥ 2 ∙
v = σ ~ T ( W ~ T ( k ) σ ~ T − 1 ( ⋯ σ ~ 1 ( W ~ 1 y ˉ k + b ~ 1 ( k ) ) ⋯ ) + b ~ T ( k ) ) \mathbf v=\tilde \sigma_{T}\left(\tilde{\mathbf W}_T^{(k)}\tilde \sigma_{T-1}\left(\cdots\tilde \sigma_1\left(\tilde {\mathbf W}_1\bar{\mathbf y}_k+\tilde{\mathbf b}_1^{(k)}\right)\cdots\right)+\tilde{\mathbf b}_T^{(k)}\right)
v = σ ~ T ( W ~ T ( k ) σ ~ T − 1 ( ⋯ σ ~ 1 ( W ~ 1 y ˉ k + b ~ 1 ( k ) ) ⋯ ) + b ~ T ( k ) )
Loss函数:对信道矩阵H \mathbf H H z ~ \tilde{\mathbf z} z ~
max x ~ , { Θ R ( k ) } k = 1 K , Θ T E H , z ~ [ ∑ k log 2 ( 1 + ∣ h k H v k ∣ 2 ∑ j ≠ k ∣ h k H v j ∣ 2 + σ 2 ) ] \max _{\tilde{\mathbf{x}},\{\Theta_{\mathrm{R}}^{(k)}\}_{k=1}^{K}, \Theta_{\mathrm{T}}} \mathbb{E}_{\mathbf{H}, \tilde{\mathbf z}}\left[\sum_{k} \log _{2}\left(1+\frac{\left|\mathbf{h}_{k}^{H} \mathbf{v}_{k}\right|^{2}}{\sum_{j \neq k}\left|\mathbf{h}_{k}^{H} \mathbf{v}_{j}\right|^{2}+\sigma^{2}}\right)\right]
x ~ , { Θ R ( k ) } k = 1 K , Θ T max E H , z ~ [ k ∑ log 2 ( 1 + ∑ j = k ∣ ∣ h k H v j ∣ ∣ 2 + σ 2 ∣ ∣ h k H v k ∣ ∣ 2 ) ]
随机梯度下降SGD
针对用户侧最后一步二值化,采用slope annealing(斜率退火)的sigmoid-adjusted straight-through(sigmoid调节直通)——用sigmoid函数去表示二值函数,从而使其可微
s g n ( u ) → 2 s i g m o i d ( α ( i ) u ) − 1 = 2 1 + exp ( − α i u ) − 1 sgn(u)\to 2\,\mathrm{sigmoid}(\alpha^{(i)}u)-1=\frac{2}{1+\exp(-\alpha^{i}u)}-1
s g n ( u ) → 2 s i g m o i d ( α ( i ) u ) − 1 = 1 + exp ( − α i u ) 2 − 1
其中,α ( i ) \alpha^{(i)} α ( i ) i i i α ( i ) ≥ α ( i − 1 ) \alpha^{(i)}\geq\alpha^{(i-1)} α ( i ) ≥ α ( i − 1 )
用户侧和BS侧均为R = T = 4 R=T=4 R = T = 4 [ 1024 , 512 , 256 , B ] [1024,512,256,B] [ 1 0 2 4 , 5 1 2 , 2 5 6 , B ] [ 1024 , 512 , 512 , 2 M K ] [1024,512,512,2MK] [ 1 0 2 4 , 5 1 2 , 5 1 2 , 2 M K ]
B(反馈的编码位数)
用户侧通过tanh输出S S S [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] Q − b i t Q-bit Q − b i t B = S × Q B=S\times Q B = S × Q
BS侧根据K S KS K S M × K M\times K M × K K B KB K B { ± 1 } \{\pm1\} { ± 1 } M × K M\times K M × K
K(用户数量)
每个用户信道分布i.i.d.,则只需要训练一个用户侧的DNN
分两个阶段:先利用单用户系统,训练导频X ~ \tilde{\mathbf X} X ~
训练的DNN具备减小频分双工多用户系统用户间干扰的能力
先估计后量化信道参数是有限导频长度下的次优解
导频长度长,能逼近最优解,且本文方法的SR一般更高
L p L_p L p
训练集和测试集的不匹配,会导致表现恶化
在更大范围的信道参数上训练DNN,能在无关于信道参数的先验条件时帮助我们设计更鲁棒的网络。
B B B 通过上面的设计,只有微不足道的损失。但同时能帮助神经网络提升在反馈容量方面的泛化能力。
K K K
DNN远好于其它有限下行链路训练资源
两步实现和end-to-end差异不大

![image-20211119104539898]()
![image-20211119111841965]()
![image-20211119111852718]()


![image-20211124123855835]()
![image-20211124164004293]()