由于没有非常系统地看完MIMO的相关内容,整理中必定有很多的问题,欢迎在评论区批评指正。
整理很乱。。。
由于网页公式渲染器KaTeX不支持公式交叉引用,我的前端水平就不足以把我这个模板加入mathjax。故将所有公式交叉引用均删除了,有的是在显示不出来的建议贴到markdown里面去吧
大规模MIMO下行链路预编码(1)_月半 月半的博客-CSDN博客
大规模MIMO下行链路预编码(2)_月半 月半的博客-CSDN博客
由于可以平衡系统性能和计算复杂度,最大比传输(MRT)预编码【又称作匹配滤波器(MF)预编码】是最简单易实现的预编码算法,通过最大化接收信噪比(SNR)实现。在大规模MIMO系统中,当基站天线数M MM足够大时,最简单的MRT线性预编码方案便可以得到最优的系统性能。
在发射端已知完美信道状态信息的前提下,MRT线性预编码矩阵为:
V = β M R T H H \mathbf V=\beta_{MRT}\mathbf H^H
V = β M R T H H
(注:以上编码矩阵后可以加上功率分配矩阵组成整个预编码矩阵)
式中, β M R T = 1 t r ( H H H ) \beta_{MRT}=\sqrt{\frac{1}{tr(HH^H )}} β M R T = t r ( H H H ) 1
传统MIMO系统中,匹配滤波预编码方案的侧重点在于接收端用户的信号增益最大化,但在多用户系统的场景下,随着传输信道相关性的提升,此方案由于没有考虑如何对用户间的干扰进行处理,将会导致整个系统性能快速下降 。
转化为互相独立的并行信道,不考虑其它信道的干扰。h i H w ~ j = 0 , i ≠ j {\bf h}_i^H\tilde{\bf w}_j=0,i\neq j h i H w ~ j = 0 , i = j
W Z F = H H ( H H H ) − 1 \mathbf{W}_{\mathrm{ZF}}=\mathbf{H}^{H}\left(\mathbf{H} \mathbf{H}^{H}\right)^{-1}
W Z F = H H ( H H H ) − 1
平均分配能量——normalized=power allocate
w ~ i = η w i η = P t r { W Z F W Z F H } \begin{gathered}
\tilde{\bf w}_i=\eta{\bf w}_i\\
\eta=\sqrt{\frac{P}{tr\{\mathbf{W}_{\mathrm{ZF}}\mathbf{W}_{\mathrm{ZF}}^H\}}}
\end{gathered}
w ~ i = η w i η = t r { W Z F W Z F H } P
信噪比高的多分配能量
maximize p 1 , … , p K ∑ i = 1 K log ( 1 + ρ i p i ) subject to ∑ i = 1 K γ i p i ≤ P , p i ≥ 0 \begin{aligned}
&\operatorname{maximize}_{p_{1}, \ldots, p_{K}} &\sum_{i=1}^{K} \log \left(1+\rho_{i} p_{i}\right) \\
&\text { subject to } & \sum_{i=1}^{K} \gamma_{i} p_{i} \leq P , p_{i} \geq 0
\end{aligned}
m a x i m i z e p 1 , … , p K subject to i = 1 ∑ K log ( 1 + ρ i p i ) i = 1 ∑ K γ i p i ≤ P , p i ≥ 0
其中,γ i = [ ( H H H ) − 1 ] \gamma_i=[({\bf HH}^H)^{-1}] γ i = [ ( H H H ) − 1 ] η i = p i \eta_i=\sqrt{p_i} η i = p i
p i = [ μ γ i − 1 ρ i ] + , ∀ i p_i=\left[\frac{\mu}{\gamma_i}-\frac{1}{\rho_i}\right]^+,\forall i
p i = [ γ i μ − ρ i 1 ] + , ∀ i
其中, [ x ] + = m a x ( x , 0 ) [x]^+=max(x,0) [ x ] + = m a x ( x , 0 )
∑ i = 1 K = [ μ − γ i ρ i − 1 ] + = P \sum_{i=1}^K=\left[\mu-\gamma_i\rho_i^{-1}\right]^+=P
i = 1 ∑ K = [ μ − γ i ρ i − 1 ] + = P
( H H H ) − 1 (\mathbf{H} \mathbf{H}^{H})^{-1} ( H H H ) − 1
W R Z F = H H ( H H H + α I ) − 1 \mathbf{W}_{\mathrm{RZF}}=\mathbf{H}^{H}\left(\mathbf{H} \mathbf{H}^{H}+\alpha \mathbf{I}\right)^{-1}
W R Z F = H H ( H H H + α I ) − 1
W ~ = η W RZF η = P t r { W R Z F W R Z F H } \begin{gathered}
\tilde{\bf W}=\eta{\bf W}_\text{RZF}\\
\eta=\sqrt{\frac{P}{tr\{\mathbf{W}_{\mathrm{RZF}}\mathbf{W}_{\mathrm{RZF}}^H\}}}
\end{gathered}
W ~ = η W RZF η = t r { W R Z F W R Z F H } P
homogeneous SNR conditions(ρ i = 1 \rho_i=1 ρ i = 1
α ⋆ = K P \alpha^{\star}=\frac KP
α ⋆ = P K
non-homogeneous SNR conditions——non-weighted sum-MSE minimization(9)W R Z F = H H ( H H H + ∑ i = 1 K ( 1 / ρ i ) P I ) − 1 \mathbf{W}_{\mathrm{RZF}}=\mathbf{H}^{H}\left(\mathbf{HH}^{H}+\frac{\sum_{i=1}^{K}\left(1 / \rho_{i}\right)}{P} \mathbf{I}\right)^{-1}
W R Z F = H H ( H H H + P ∑ i = 1 K ( 1 / ρ i ) I ) − 1
解决非凸问题的数值算法。weighted MSE problem(10)
minimize Λ , Ω , W ~ E { ∥ Ω 1 2 ( u − Λ y ) ∥ 2 } − log det Ω subject to Tr { W ~ W ~ H } ≤ P \begin{aligned}
&\underset{\Lambda, \Omega, \tilde{\mathbf{W}}}{\operatorname{minimize}} \mathbb{E}\left\{\left\|\Omega^{\frac{1}{2}}(\mathbf{u}-\Lambda \mathbf{y})\right\|^{2}\right\}-\log \operatorname{det} \Omega \\
&\text { subject to } \operatorname{Tr}\left\{\tilde{\mathbf{W}} \tilde{\mathbf{W}}^{H}\right\} \leq P
\end{aligned}
Λ , Ω , W ~ m i n i m i z e E { ∥ ∥ ∥ Ω 2 1 ( u − Λ y ) ∥ ∥ ∥ 2 } − log d e t Ω subject to T r { W ~ W ~ H } ≤ P
其中,Ω , Λ \mathbf{\Omega},\mathbf{\Lambda} Ω , Λ Ω \mathbf{\Omega} Ω Λ \mathbf{\Lambda} Λ W ~ , Ω , Λ \tilde{\mathbf{W}},\mathbf{\Omega},\mathbf{\Lambda} W ~ , Ω , Λ
S1:随机初始化变量
∣ ∣ w ~ i ∣ ∣ 2 = P K ||\tilde{\mathbf{w}}_i||^2=\frac PK
∣ ∣ w ~ i ∣ ∣ 2 = K P
S2:迭代直到convergence
确定W ~ , Ω \tilde{\mathbf{W}},\mathbf{\Omega} W ~ , Ω Λ \mathbf{\Lambda} Λ
λ i = arg min λ i E { ∣ u i − λ i y i ∣ 2 } = ( ∑ j = 1 K ρ i ∣ h i H w ~ j ∣ 2 + 1 ) − 1 ρ i w ~ i H h i . \begin{aligned}
\lambda_{i} &=\arg \min _{\lambda_{i}} \mathbb{E}\left\{\left|u_{i}-\lambda_{i} y_{i}\right|^{2}\right\} \\
&=\left(\sum_{j=1}^{K} \rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+1\right)^{-1} \sqrt{\rho_{i}} \tilde{\mathbf{w}}_{i}^{H} \mathbf{h}_{i} .
\end{aligned}
λ i = arg λ i min E { ∣ u i − λ i y i ∣ 2 } = ( j = 1 ∑ K ρ i ∣ ∣ h i H w ~ j ∣ ∣ 2 + 1 ) − 1 ρ i w ~ i H h i .
确定W ~ , Λ \tilde{\mathbf{W}},\mathbf{\Lambda} W ~ , Λ Ω \mathbf{\Omega} Ω
ω i = arg min ω i ω i e i − log ω i = e i − 1 = 1 + SINR i = ∑ j = 1 K ρ i ∣ h i H w ~ j ∣ 2 + 1 ∑ j ≠ i K ρ i ∣ h i H w ~ j ∣ 2 + 1 \begin{aligned}
\omega_{i} &=\arg \min _{\omega_{i}} \omega_{i} e_{i}-\log \omega_{i} \\
&=e_{i}^{-1}=1+\operatorname{SINR}_{i}=\frac{\sum_{j=1}^{K} \rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+1}{\sum_{j \neq i}^{K} \rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+1}
\end{aligned}
ω i = arg ω i min ω i e i − log ω i = e i − 1 = 1 + S I N R i = ∑ j = i K ρ i ∣ ∣ h i H w ~ j ∣ ∣ 2 + 1 ∑ j = 1 K ρ i ∣ ∣ h i H w ~ j ∣ ∣ 2 + 1
确定Ω , Λ \mathbf{\Omega},\mathbf{\Lambda} Ω , Λ W ~ \tilde{\mathbf{W}} W ~
W ~ = ( H H Λ H Ω Σ Λ H + μ I ) − 1 H H Λ H Ω Σ 1 2 = H H [ H H H + μ ( Λ H Ω Σ Λ ) − 1 ] − 1 Λ − 1 Σ − 1 2 \begin{aligned}
\tilde{\mathbf{W}} &=\left(\mathbf{H}^{H} \Lambda^{H} \Omega \Sigma \Lambda \mathbf{H}+\mu \mathbf{I}\right)^{-1} \mathbf{H}^{H} \Lambda^{H} \Omega \Sigma^{\frac{1}{2}} \\
&=\mathbf{H}^{H}\left[\mathbf{H} \mathbf{H}^{H}+\mu\left(\Lambda^{H} \Omega \Sigma \Lambda\right)^{-1}\right]^{-1} \Lambda^{-1} \Sigma^{-\frac{1}{2}}
\end{aligned}
W ~ = ( H H Λ H Ω Σ Λ H + μ I ) − 1 H H Λ H Ω Σ 2 1 = H H [ H H H + μ ( Λ H Ω Σ Λ ) − 1 ] − 1 Λ − 1 Σ − 2 1
MMSE precoding for multiuser MISO downlink transmission with non-homogeneous user SNR conditions
MU-MISO模型(M天线、K用户)
u \bf u u U E i UE_i U E i u i u_i u i
y = Σ 1 2 H W ~ u + n x = ∑ i = 1 K w ~ i u i = u W ~ \begin{gathered}
\mathbf{y}=\mathbf{\Sigma}^{\frac 12}\mathbf{H\tilde Wu}+\mathbf{n}\\
\mathbf{x}=\sum_{i=1}^K\tilde{\mathbf{w}}_iu_i=\mathbf{u\tilde W}
\end{gathered}
y = Σ 2 1 H W ~ u + n x = i = 1 ∑ K w ~ i u i = u W ~
其中,Σ = d i a g ( ρ 1 , ⋯ , ρ K ) \mathbf{\Sigma}=\mathrm{diag}(\rho_1,\cdots,\rho_K) Σ = d i a g ( ρ 1 , ⋯ , ρ K ) H = [ h 1 , ⋯ , h K ] H \mathbf{H}=[\mathbf{h}_1,\cdots,\mathbf{h}_K]^H H = [ h 1 , ⋯ , h K ] H W ~ = [ w ~ 1 , ⋯ , w ~ K ] \tilde{\mathbf{W}}=[\tilde{\mathbf{w}}_1,\cdots,\tilde{\mathbf{w}}_K] W ~ = [ w ~ 1 , ⋯ , w ~ K ] u = [ u 1 , ⋯ , u K ] T u=[u_1,\cdots,u_K]^T u = [ u 1 , ⋯ , u K ] T
SINR(信干噪比)
S I N R i = ρ i ∣ h i H w ~ i ∣ 2 ∑ j ≠ i K ρ i ∣ h i H w ~ j ∣ 2 + 1 \mathrm{SINR}_i=\frac{\rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{i}\right|^{2}}{\sum_{j \neq i}^{K} \rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+1}
S I N R i = ∑ j = i K ρ i ∣ ∣ h i H w ~ j ∣ ∣ 2 + 1 ρ i ∣ ∣ h i H w ~ i ∣ ∣ 2
sum-rate的优化问题——非凸问题
maximize w ~ 1 , … , w ~ K ∑ i = 1 K log ( 1 + ρ i ∣ h i H w ~ i ∣ 2 ∑ j ≠ i K ρ i ∣ h i H w ~ j ∣ 2 + 1 ) subject to ∑ i = 1 K ∥ w ~ i ∥ 2 ≤ P \begin{aligned}
&\underset{\tilde{\mathbf{w}}_{1}, \ldots, \tilde{\mathbf{w}}_{K}}{\operatorname{maximize}} \sum_{i=1}^{K} \log \left(1+\frac{\rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{i}\right|^{2}}{\sum_{j \neq i}^{K} \rho_{i}\left|\mathbf{h}_{i}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+1}\right) \\
&\text { subject to } \sum_{i=1}^{K}\left\|\tilde{\mathbf{w}}_{i}\right\|^{2} \leq P
\end{aligned}
w ~ 1 , … , w ~ K m a x i m i z e i = 1 ∑ K log ( 1 + ∑ j = i K ρ i ∣ ∣ h i H w ~ j ∣ ∣ 2 + 1 ρ i ∣ ∣ h i H w ~ i ∣ ∣ 2 ) subject to i = 1 ∑ K ∥ w ~ i ∥ 2 ≤ P
take advantage of the non-homogeneous SNR conditions at the UE to predetermine the weights and receive coefficients and thus remove the iterative procedure of the IWMMSE algorithm.(利用UE的信噪比非同质这一特点,事先确定IWMMSE中的两个迭代参数Ω , Λ \mathbf{\Omega},\mathbf{\Lambda} Ω , Λ
用effective small-scale channel gain G ( g i = ∣ ∣ h i ∣ ∣ σ n i ) \mathbf{G}(g_i=\frac{||\mathbf{h}_i||}{\sigma_{n_i}}) G ( g i = σ n i ∣ ∣ h i ∣ ∣ )
M S E = E { ∥ G Σ 1 2 ⏟ Ω 1 2 ( u − η − 1 G − 1 Σ − 1 2 ⏟ Λ y ) ∥ 2 } \mathrm{MSE}=\mathbb{E}\left\{\left\|\underbrace{\mathbf{G} \boldsymbol{\Sigma}^{\frac{1}{2}}}_{\mathbf{\Omega}^{\frac12}}\left(\mathbf{u}-\underbrace{\eta^{-1} \mathbf{G}^{-1} \boldsymbol{\Sigma}^{-\frac{1}{2}}}_{\Lambda} \mathbf{y}\right)\right\|^{2}\right\}
M S E = E ⎩ ⎪ ⎨ ⎪ ⎧ ∥ ∥ ∥ ∥ ∥ ∥ Ω 2 1 G Σ 2 1 ⎝ ⎛ u − Λ η − 1 G − 1 Σ − 2 1 y ⎠ ⎞ ∥ ∥ ∥ ∥ ∥ ∥ 2 ⎭ ⎪ ⎬ ⎪ ⎫
使用lagrange乘数法求lagrange因子μ ⋆ \mu^{\star} μ ⋆ W ⋆ \mathbf{W}^{\star} W ⋆
μ ⋆ = K P W ⋆ = H H ( H H H + K P Σ − 1 ) − 1 G \begin{gathered}\mu^\star=\frac KP\\
\mathbf{W}^\star=\mathbf{H}^H\left(\mathbf{HH}^H+\frac KP\mathbf{\Sigma}^{-1}\right)^{-1}\mathbf{G}
\end{gathered}
μ ⋆ = P K W ⋆ = H H ( H H H + P K Σ − 1 ) − 1 G
结果与IWMMSE形式类似,与RZF相比采用non-identity regularizer matrix(非同一正则矩阵)
对平均SNR无knowledge。
CDI(channel direction indicator):量化方向矢量h ^ i \mathbf{\hat h}_i h ^ i h ^ i \mathbf{\hat h}_i h ^ i h i \mathbf{h}_i h i
CQI(channel quality indicator):用有效信道增益表示瞬时信噪比g ^ i ρ ^ i = M P S N R i ^ \hat g_i \hat \rho_i=\frac MP\widehat{SNR_i} g ^ i ρ ^ i = P M S N R i ρ i \rho_i ρ i
CDI和CQI综合即可改写式\eqref{eq:16} ,但量化误差会带来non-robust。
分解归一化信道h ~ i = h i ∣ ∣ h i ∣ ∣ \mathbf{\tilde h}_i=\frac{\mathbf{h}_i}{||\mathbf{h}_i||} h ~ i = ∣ ∣ h i ∣ ∣ h i
h ~ i = 1 − z i h ^ i + z i s z i = 1 − ∣ h ~ i H h ^ i ∣ 2 \begin{gathered}
\mathbf{\tilde h}_i=\sqrt{1-z_i}\,\mathbf{\hat h}_i+\sqrt{z_i}\,\mathbf{s}\\
z_i=1-|\mathbf{\tilde h}_i^H\mathbf{\hat h}_i|^2
\end{gathered}
h ~ i = 1 − z i h ^ i + z i s z i = 1 − ∣ h ~ i H h ^ i ∣ 2
其中,z i z_i z i h ~ i \mathbf{\tilde h}_i h ~ i h ^ i \mathbf{\hat h}_i h ^ i s \mathbf{s} s h ^ i \mathbf{\hat h}_i h ^ i
和perfect CSI and average SNR knowledge的MSE一致,但是其中H ~ \mathbf{\tilde H} H ~
H = G H ~ = G ( I − Z ) 1 2 H ^ + G Z 1 2 S \mathbf{H}=\mathbf{G} \tilde{\mathbf{H}}=\mathbf{G}(\mathbf{I}-\mathbf{Z})^{\frac{1}{2}} \hat{\mathbf{H}}+\mathbf{G} \mathbf{Z}^{\frac{1}{2}} \mathbf{S}
H = G H ~ = G ( I − Z ) 2 1 H ^ + G Z 2 1 S
化开,同样使用lagrange乘数法求lagrange因子μ ⋆ \mu^{\star} μ ⋆ W ⋆ \mathbf{W}^{\star} W ⋆
μ ⋆ \mu^\star μ ⋆
W = ζ 1 − δ H ^ H ( H ^ H ^ H + δ P Tr { Σ G 2 } + K M P M ( 1 − δ ) Σ − 1 G − 2 ) − 1 \mathbf{W}=\frac{\zeta}{1-\delta} \hat{\mathbf{H}}^{H}\left(\hat{\mathbf{H}} \hat{\mathbf{H}}^{H}+\frac{\delta P \operatorname{Tr}\left\{\mathbf{\Sigma G}^{2}\right\}+K M}{P M(1-\delta)} \mathbf{\Sigma}^{-1} \mathbf{G}^{-2}\right)^{-1}
W = 1 − δ ζ H ^ H ( H ^ H ^ H + P M ( 1 − δ ) δ P T r { Σ G 2 } + K M Σ − 1 G − 2 ) − 1
系数不影响归一化的波束成形矩阵W ~ \mathbf{\tilde W} W ~ S N R = P M G 2 Σ \mathbf{SNR}=\frac PM\mathbf{G}^2\mathbf{\Sigma} S N R = M P G 2 Σ
W ⋆ = H ^ H ( H ^ H ^ H + δ Tr { S N R } + K M ( 1 − δ ) S N R − 1 ) − 1 \mathbf{W}^\star=\hat{\mathbf{H}}^{H}\left(\hat{\mathbf{H}} \hat{\mathbf{H}}^{H}+\frac{\delta \operatorname{Tr}\left\{\mathbf{SNR}\right\}+K }{M(1-\delta)} \mathbf{SNR}^{-1}\right)^{-1}
W ⋆ = H ^ H ( H ^ H ^ H + M ( 1 − δ ) δ T r { S N R } + K S N R − 1 ) − 1
由quantized CDI and CQI feedbacks可以推perfect CSI and average SNR knowledge
CQI量化可能无法很好估计SNR
可以通过WMMSE推出non-weighted MMSE【1-[11]】
用计算的effective small-scale channel gain却代替迭代的过程。
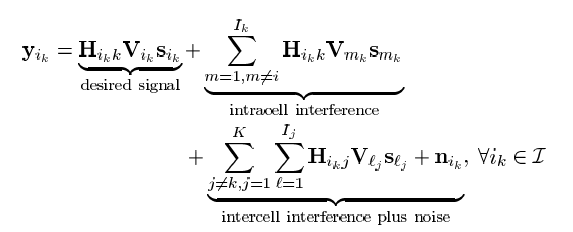
An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel
MIMO
每次给UEi k i_k i k s \bf s s
s ^ i k = U i k H y i k \mathbf{\hat s}_{i_k}=\mathbf{U}_{i_k}^H\mathbf{y}_{i_k}
s ^ i k = U i k H y i k
Sum-rate problem
在点对点单用户信道中,如果我们已知发送信号的协方差矩阵Q = E { x k x k H } \mathbf{Q}=\mathbb{E}\{\mathbf{x}_k\mathbf{x}_k^H\} Q = E { x k x k H }
log ∣ I + H Q H H ∣ . \log |\mathbf{I}+\mathbf{H}\mathbf{Q}\mathbf{H}^H|.
log ∣ I + H Q H H ∣ .
扩展到多用户IC信道,此时干扰加噪声协方差矩阵(interference-plus-noise covariance matrix)就不会再成为单位矩阵,它是R i = ∑ i ≠ j H j i Q j H j i H + I , \mathbf{R}_i = \sum_{i \neq j} \mathbf{H}_{ji}\mathbf{Q}_j \mathbf{H}_{ji}^H+\mathbf{I}, R i = ∑ i = j H j i Q j H j i H + I ,
∑ i = 1 K log ∣ I + R i − 1 H i i Q i H i i H ∣ . \sum_{i=1}^K \log |\mathbf{I}+\mathbf{R}^{-1}_i\mathbf{H}_{ii}\mathbf{Q}_i\mathbf{H}^H_{ii}|.
i = 1 ∑ K log ∣ I + R i − 1 H i i Q i H i i H ∣ .
考虑它更广义的形式i i i λ i \lambda_i λ i ρ i \rho_i ρ i
∑ i = 1 K λ i log ∣ I + R i − 1 H i i Q i H i i H ∣ \sum_{i=1}^K \lambda_i\log |\mathbf{I}+\mathbf{R}^{-1}_i\mathbf{H}_{ii}\mathbf{Q}_i\mathbf{H}^H_{ii}|
i = 1 ∑ K λ i log ∣ I + R i − 1 H i i Q i H i i H ∣
【优质信源】计划02–多用户通信中总速率优化问题的一些凸优化模式 - 知乎 (zhihu.com)
sum-rate problem(1)
max V ∑ k = 1 K ∑ i k = 1 I k α i k R i k s.t. ∑ i = 1 I k Tr ( V i k V i k H ) ≤ P k , ∀ k = 1 , 2 , … , K \begin{aligned}
\max_{\mathbf{V}} & \sum_{k=1}^{K} \sum_{i_{k}=1}^{I_{k}} \alpha_{i_{k}} R_{i_{k}} \\
\text { s.t. } & \sum_{i=1}^{I_{k}} \operatorname{Tr}\left(\mathbf{V}_{i_{k}} \mathbf{V}_{i_{k}}^{H}\right) \leq P_{k}, \forall k=1,2, \ldots, K
\end{aligned}
V max s.t. k = 1 ∑ K i k = 1 ∑ I k α i k R i k i = 1 ∑ I k T r ( V i k V i k H ) ≤ P k , ∀ k = 1 , 2 , … , K
其中,α i k \alpha_{i_k} α i k
sum-MSE minimization(4)
min U , V ∑ k = 1 K ∑ i = 1 I k Tr ( E i k ) = ∑ k = 1 K ∑ i = 1 I k ∣ ∣ s ^ i k − s i k ∣ ∣ s.t. ∑ i = 1 I k Tr ( V i k V i k H ) ≤ P k , k = 1 , 2 , … , K . \begin{aligned}
\min _{\mathbf{U}, \mathbf{V}} & \sum_{k=1}^{K} \sum_{i=1}^{I_{k}} \operatorname{Tr}\left(\mathbf{E}_{i_{k}}\right) =\sum_{k=1}^{K} \sum_{i=1}^{I_{k}} ||\mathbf{\hat s }_{i_k}-\mathbf{s}_{i_k}||\\
\text { s.t. } & \sum_{i=1}^{I_{k}} \operatorname{Tr}\left(\mathbf{V}_{i_{k}} \mathbf{V}_{i_{k}}^{H}\right) \leq P_{k}, \quad k=1,2, \ldots, K .
\end{aligned}
U , V min s.t. k = 1 ∑ K i = 1 ∑ I k T r ( E i k ) = k = 1 ∑ K i = 1 ∑ I k ∣ ∣ s ^ i k − s i k ∣ ∣ i = 1 ∑ I k T r ( V i k V i k H ) ≤ P k , k = 1 , 2 , … , K .
U i k m m s e = J i k − 1 H i k k V i k E i k m m s e = I − V i k H H i k k H J i k − 1 H i k k V i k \begin{aligned}
\mathbf{U}_{i_{k}}^{\mathrm{mmse}}=&\mathbf{J}_{i_{k}}^{-1} \mathbf{H}_{i_{k} k} \mathbf{V}_{i_{k}}\\
\mathbf{E}_{i_{k}}^{\mathrm{mmse}}=&\mathbf{I}-\mathbf{V}_{i_{k}}^{H} \mathbf{H}_{i_{k} k}^{H} \mathbf{J}_{i_{k}}^{-1} \mathbf{H}_{i_{k} k} \mathbf{V}_{i_{k}}
\end{aligned}
U i k m m s e = E i k m m s e = J i k − 1 H i k k V i k I − V i k H H i k k H J i k − 1 H i k k V i k
其中,J i k ≜ ∑ j = 1 K ∑ ℓ = 1 I j H i k j V ℓ j V ℓ j H H i k H + σ i k 2 I \mathbf{J}_{i_{k}} \triangleq \sum_{j=1}^{K} \sum_{\ell=1}^{I_{j}} \mathbf{H}_{i_{k} j} \mathbf{V}_{\ell_{j}} \mathbf{V}_{\ell_{j}}^{H} \mathbf{H}_{i_{k}}^{H}+\sigma_{i_{k}}^{2} \mathbf{I} J i k ≜ ∑ j = 1 K ∑ ℓ = 1 I j H i k j V ℓ j V ℓ j H H i k H + σ i k 2 I
两个问题的统一性(7)——【1-[5]、2-[13]】梯度、KKT条件引出
min W , U , V ∑ k = 1 K ∑ i = 1 I k α i k ( Tr ( W i k E i k ) − log det ( W i k ) ) s.t. ∑ i = 1 I k Tr ( V i k V i k H ) ≤ P k , k = 1 , 2 , … , K \begin{aligned}
\min _{\mathbf{W}, \mathbf{U}, \mathbf{V}} & \sum_{k=1}^{K} \sum_{i=1}^{I_{k}} \alpha_{i_{k}}\left(\operatorname{Tr}\left(\mathbf{W}_{i_{k}} \mathbf{E}_{i_{k}}\right)-\log \operatorname{det}\left(\mathbf{W}_{i_{k}}\right)\right) \\
\text { s.t. } & \sum_{i=1}^{I_{k}} \operatorname{Tr}\left(\mathbf{V}_{i_{k}} \mathbf{V}_{i_{k}}^{H}\right) \leq P_{k}, k=1,2, \ldots, K
\end{aligned}
W , U , V min s.t. k = 1 ∑ K i = 1 ∑ I k α i k ( T r ( W i k E i k ) − log d e t ( W i k ) ) i = 1 ∑ I k T r ( V i k V i k H ) ≤ P k , k = 1 , 2 , … , K
(7) is in the space of ( u , v , w ) (u,v,w) ( u , v , w )
R i k = log det ( ( E i k m m s e ) − 1 ) R_{i_k}=\log\det\left(\left(\mathbf{E}_{i_k}^{mmse}\right)^{-1}\right)
R i k = log det ( ( E i k m m s e ) − 1 )
要解决sum-rate问题,即解决式\eqref{eq:2-7}的优化问题,需要优化U , V , W \mathbf{U,V,W} U , V , W
1 Initialize V i k \mathbf{V}_{i_{k}} V i k Tr ( V i k V i k H ) = p k I k \operatorname{Tr}\left(\mathbf{V}_{i_{k}} \mathbf{V}_{i_{k}}^{H}\right)=\frac{p_{k}}{I_{k}} T r ( V i k V i k H ) = I k p k repeat 3 W i k ′ ← W i k , ∀ i k ∈ I 3 \quad \mathbf{W}_{i_{k}}^{\prime} \leftarrow \mathbf{W}_{i_{k}}, \quad \forall i_{k} \in \mathcal{I} 3 W i k ′ ← W i k , ∀ i k ∈ I 4 U i k ← ( ∑ ( j , ℓ ) H i k j V ℓ j V ℓ j H H i k j H + σ i k 2 I ) − 1 H i k k V k , ∀ i k ∈ I 4 \quad \mathbf{U}_{i_{k}} \leftarrow\left(\sum_{(j, \ell)} \mathbf{H}_{i_{k} j} \mathbf{V}_{\ell_{j}} \mathbf{V}_{\ell_{j}}^{H} \mathbf{H}_{i_{k} j}^{H}+\sigma_{i_{k}}^{2} \mathbf{I}\right)^{-1} \mathbf{H}_{i_{k} k} \mathbf{V}_{k}, \forall i_{k} \in \mathcal{I} 4 U i k ← ( ∑ ( j , ℓ ) H i k j V ℓ j V ℓ j H H i k j H + σ i k 2 I ) − 1 H i k k V k , ∀ i k ∈ I 5 W i k ← ( I − U i k H H i k k V i k ) − 1 , ∀ i k ∈ I 5\quad\mathbf{W}_{i_{k}} \leftarrow\left(\mathbf{I}-\mathbf{U}_{i_{k}}^{H} \mathbf{H}_{i_{k} k} \mathbf{V}_{i_{k}}\right)^{-1}, \forall i_{k} \in \mathcal{I} 5 W i k ← ( I − U i k H H i k k V i k ) − 1 , ∀ i k ∈ I 6 V i k ← α i k ( ∑ ( j , ℓ ) α ℓ j H ℓ j k H U ℓ j W ℓ j U ℓ j H H ℓ j k + μ k ∗ I ) − 1 H i k k H U i k W i k , ∀ i k 6 \quad \mathbf{V}_{i_{k}} \leftarrow \alpha_{i_{k}}\left(\sum_{(j, \ell)} \alpha_{\ell_{j}} \mathbf{H}_{\ell_{j} k}^{H} \mathbf{U}_{\ell_{j}} \mathbf{W}_{\ell_{j}} \mathbf{U}_{\ell_{j}}^{H} \mathbf{H}_{\ell_{j} k}+\mu_{k}^{*} \mathbf{I}\right)^{-1} \mathbf{H}_{i_{k} k}^{H} \mathbf{U}_{i_{k}} \mathbf{W}_{i_{k}}, \forall i_{k} 6 V i k ← α i k ( ∑ ( j , ℓ ) α ℓ j H ℓ j k H U ℓ j W ℓ j U ℓ j H H ℓ j k + μ k ∗ I ) − 1 H i k k H U i k W i k , ∀ i k until ∣ ∑ ( j , ℓ ) log det ( W ℓ j ) − ∑ ( j , ℓ ) log det ( W ℓ j ′ ) ∣ ≤ ϵ \left|\sum_{(j, \ell)} \log \operatorname{det}\left(\mathbf{W}_{\ell_{j}}\right)-\sum_{(j, \ell)} \log \operatorname{det}\left(\mathbf{W}_{\ell_{j}}^{\prime}\right)\right| \leq \epsilon ∣ ∣ ∣ ∑ ( j , ℓ ) log d e t ( W ℓ j ) − ∑ ( j , ℓ ) log d e t ( W ℓ j ′ ) ∣ ∣ ∣ ≤ ϵ
W \mathbf{W} W W \mathbf{W} W W ⋆ = ( E i k M M S E ) − 1 \mathbf{W}^\star=(\mathbf{E}_{i_k}^{MMSE})^{-1} W ⋆ = ( E i k M M S E ) − 1 E i k M M S E \mathbf{E}_{i_k}^{MMSE} E i k M M S E U \mathbf{U} U U \mathbf{U} U U \mathbf{U} U V \mathbf{V} V V \mathbf{V} V V \mathbf{V} V μ k \mu_k μ k μ k ⋆ \mu_k^\star μ k ⋆
这种方法也适用于general utility maximization
(7) is in the space of ( u , v , w ) (u,v,w) ( u , v , w )
the sum-rate maximization problem is first equivalently transformed into an MMSE problem and then a block coordinate descent (BCD) method is proposed to solve the resultant MMSE problem.
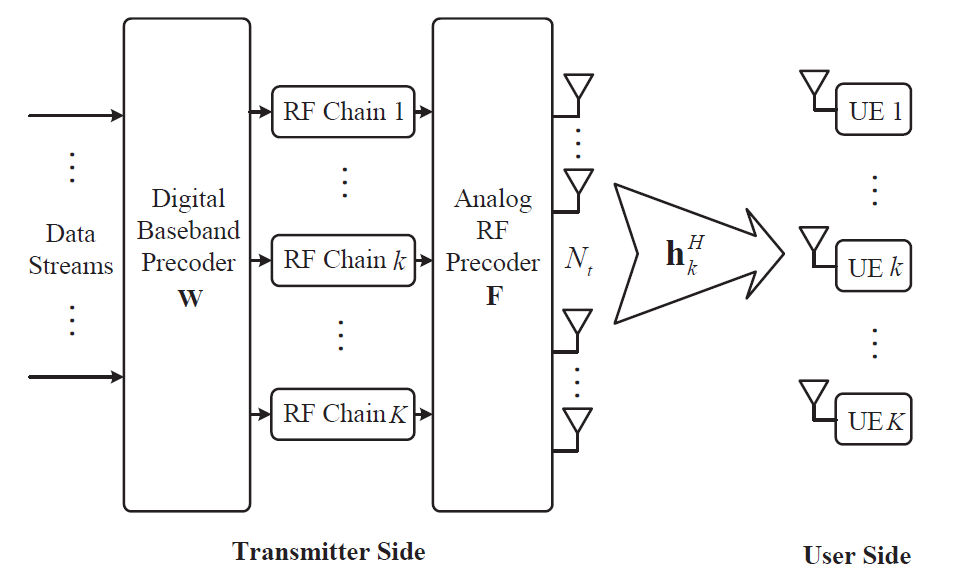
混合预编码——传统数字预编码的RF chain数量需要和N t N_t N t W F \mathbf{WF} W F
y k = h k H F N t × K W K × K s K × 1 + n k y_k=\mathbf{h}_k^H\mathbf{F}_{N_t\times K}\mathbf{W}_{K\times K}\mathbf{s}_{K\times 1}+n_k
y k = h k H F N t × K W K × K s K × 1 + n k
apply phase-only control to couple the K K K N t N_t N t F \mathbf{F} F N t N_t N t
F \bf F F
F i , j = 1 N t e j φ i , j \mathbf{F}_{i,j}=\frac{1}{\sqrt{N_t}}e^{j\varphi_{i,j}}
F i , j = N t 1 e j φ i , j
This is to align the phases of channel elements and can thus harvest the large array gain provided by the massive multiuser MIMO systems.
W \bf W W H F \bf HF H F H \bf H H
W = H e q H ( H e q H e q H ) − 1 Λ \mathbf{W}=\mathbf{H}_{eq}^H(\mathbf{H}_{eq}\mathbf{H}_{eq}^H)^{-1}\mathbf{\Lambda}
W = H e q H ( H e q H e q H ) − 1 Λ
Λ \mathbf{\Lambda} Λ η i \eta_i η i
Quantized RF Phase Control:由于F \mathbf{F} F W \mathbf{W} W F ^ \mathbf{\hat F} F ^
——当N t N_t N t
Phased-ZF的上界R ≤ K R R\leq K \mathcal{R} R ≤ K R
lim N t → ∞ R log 2 ( 1 + π 4 P N t K ) = 1 R = E [ 1 + P K ∣ h k H f k ∣ 2 ] \begin{gathered}
\lim_{N_t\to \infty}\frac{\mathcal{R}}{\log_2\left(1+\frac{\pi}{4}\frac{PN_t}{K}\right)}=1\\
\mathcal{R}=\mathbb{E}\left[1+\frac PK |\mathbf{h}_k^H\mathbf{f}_k|^2\right]
\end{gathered}
N t → ∞ lim log 2 ( 1 + 4 π K P N t ) R = 1 R = E [ 1 + K P ∣ h k H f k ∣ 2 ]
1 2 3 4 5 6 F = 1 /sqrt (Nt)*exp (j .*angle (H))'; Fb = CalBDPrecoder(H*F); wt = F*Fb; WPR = wt*inv(sqrt (diag (diag (wt'*wt)))); rateHyb(isnr) = rateHyb(isnr) + CalRate((P/K)*eye (K), H, WPR);
毫米波信道的特点:limited multipath components.—— poor scattering nature
h k H = N t N p ∑ l = 1 N p α l k a H ( ϕ l k , θ l k ) \mathbf{h}_k^H=\sqrt{\frac{N_t}{N_p}}\sum_{l=1}^{N_p}\alpha_l^k\mathbf{a}^H(\phi_l^k,\theta_l^k)
h k H = N p N t l = 1 ∑ N p α l k a H ( ϕ l k , θ l k )
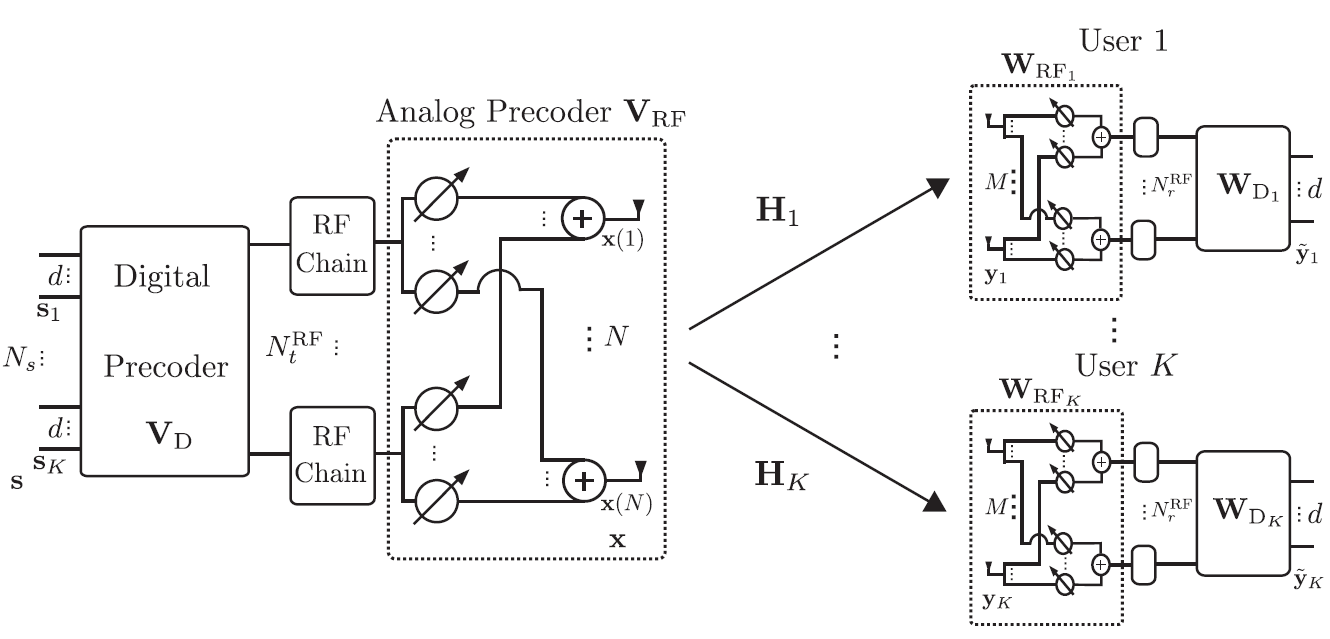
在性能减弱不大的情况下,减少射频链(RF chains)的数量
x = V R F ⏟ N × N t R F V D ⏟ N t R F × N s s = ∑ ℓ = 1 K V R F V D ℓ s ℓ \mathbf{x}=\underbrace{\mathbf{V}_{RF}}_{N\times N_t^{RF}}\underbrace{\mathbf{V}_D}_{N_t^{RF}\times N_s}\mathbf{s}=\sum_{\ell=1}^K\mathbf{V}_{RF}\mathbf{V}_{D_\ell}\mathbf{s}_\ell
x = N × N t R F V R F N t R F × N s V D s = ℓ = 1 ∑ K V R F V D ℓ s ℓ
其中,N s = K d N_s=Kd N s = K d K K K d d d
接收信号
s ~ k = y ~ k = W t k H H k V t k s k ⏟ desired signals + W t k H H k ∑ ℓ ≠ k V t ℓ s ℓ ⏟ effective interference + W t k H z k ⏟ effective noise \mathbf{\tilde s}_k=\tilde{\mathbf{y}}_{k}=\underbrace{\mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{H}_{k} \mathbf{V}_{\mathrm{t}_{k}} \mathbf{s}_{k}}_{\text {desired signals }}+\underbrace{\mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{H}_{k} \sum_{\ell \neq k} \mathbf{V}_{\mathrm{t}_{\ell}} \mathbf{s}_{\ell}}_{\text {effective interference }}+\underbrace{\mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{z}_{k}}_{\text {effective noise }}
s ~ k = y ~ k = desired signals W t k H H k V t k s k + effective interference W t k H H k ℓ = k ∑ V t ℓ s ℓ + effective noise W t k H z k
其中,基站的预编码V t k = V R F V D k \mathbf{V}_{\mathrm{t}_k}=\mathbf{V}_{RF}\mathbf{V}_{D_k} V t k = V R F V D k W t k = V R F k V D k \mathbf{W}_{\mathrm{t}_k}=\mathbf{V}_{RF_k}\mathbf{V}_{D_k} W t k = V R F k V D k
优化问题sum-rate problem(4)
R k = log 2 ∣ I M + W t k C k − 1 W t k H H k V t k V t k H H k H ∣ where C k = W t k H H k ( ∑ ℓ ≠ k V t ℓ V t ℓ H ) H k H W t k + σ 2 W t k H W t k \begin{aligned}
&R_{k}=\log _{2}\left|\mathbf{I}_{M}+\mathbf{W}_{\mathrm{t}_{k}} \mathbf{C}_{k}^{-1} \mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{H}_{k} \mathbf{V}_{\mathrm{t}_{k}} \mathbf{V}_{\mathrm{t}_{k}}^{H} \mathbf{H}_{k}^{H}\right|\\
&\text { where } \quad \mathbf{C}_{k}=\mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{H}_{k}\left(\sum_{\ell \neq k} \mathbf{V}_{\mathrm{t}_{\ell}} \mathbf{V}_{\mathrm{t}_{\ell}}^{H}\right) \mathbf{H}_{k}^{H} \mathbf{W}_{\mathrm{t}_{k}}+\sigma^{2} \mathbf{W}_{\mathrm{t}_{k}}^{H} \mathbf{W}_{\mathrm{t}_{k}}
\end{aligned}
R k = log 2 ∣ ∣ I M + W t k C k − 1 W t k H H k V t k V t k H H k H ∣ ∣ where C k = W t k H H k ⎝ ⎛ ℓ = k ∑ V t ℓ V t ℓ H ⎠ ⎞ H k H W t k + σ 2 W t k H W t k
Point-to-Point MIMO——两侧都是大规模天线阵列
下行链路MU-MIMO——基站侧多天线,用户侧单天线
V F D ∈ C N × N s \mathbf{V}_{FD}\in \mathbb{C}^{N\times N_s} V F D ∈ C N × N s
必要条件:N R F ≥ N s N^{RF}\geq N_s N R F ≥ N s
充分条件:N R F ≥ 2 N s N^{RF}\geq 2N_s N R F ≥ 2 N s
N s ≥ 2 N R F N_s\geq 2N^{RF} N s ≥ 2 N R F N s N_s N s 2 N s N 2N_sN 2 N s N 当N R F ≈ N N^{RF}\approx N N R F ≈ N N s N N_sN N s N
在低信噪比环境中,若V F D \mathbf{V}_{FD} V F D V F D = A N × r B r × N s \mathbf{V}_{FD}=\mathbf{A}_{N\times r}\mathbf{B}_{r\times N_s} V F D = A N × r B r × N s A = V R F V D ′ \mathbf{A}=\mathbf{V}_{RF}\mathbf{V}'_D A = V R F V D ′ 2 r 2r 2 r V R F \mathbf{V}_{RF} V R F V D ′ B \mathbf{V}'_D\mathbf{B} V D ′ B
假设N t R F = N r R F = N R F N_t^{RF}=N_r^{RF}=N^{RF} N t R F = N r R F = N R F
优化目标:由\eqref{eq:4-4}化简:
R = log 2 ∣ I M + 1 σ 2 W t ( W t H W t ) − 1 W t H H V t V t H H H ∣ R=\log _{2}\left|\mathbf{I}_{M}+\frac{1}{\sigma^2}\mathbf{W}_{\mathrm{t}} (\mathbf{W}_t^H\mathbf{W}_t)^{-1} \mathbf{W}_{\mathrm{t}}^{H} \mathbf{H} \mathbf{V}_{\mathrm{t}} \mathbf{V}_{\mathrm{t}}^{H} \mathbf{H}^{H}\right|
R = log 2 ∣ ∣ ∣ ∣ I M + σ 2 1 W t ( W t H W t ) − 1 W t H H V t V t H H H ∣ ∣ ∣ ∣
考虑用户间干扰的因素
考虑streams的优先级
proposes a design for the scenarios where N R F > K N^{RF} > K N R F > K N N N
方法:在V R F \mathbf{V}_{RF} V R F P \mathbf{P} P
先优化V R F = e − j θ i , j \mathbf{V}_{RF}=e^{-j\theta_{i,j}} V R F = e − j θ i , j
V R F \mathbf{V}_{RF} V R F
P = d i a g ( p 1 , ⋯ , p k ) p k = 1 q ~ k k ( β k λ − q ~ k k σ 2 ) + \begin{gathered}
\mathbf{P}=\mathrm{diag}(p_1,\cdots,p_k)\\
p_k=\frac{1}{\tilde q_{kk}}\left(\frac{\beta_k}{\lambda}-\tilde q_{kk}\sigma^2\right)^+
\end{gathered}
P = d i a g ( p 1 , ⋯ , p k ) p k = q ~ k k 1 ( λ β k − q ~ k k σ 2 ) +
其中,q ~ k k \tilde q_{kk} q ~ k k DH\mathbf{V}_{RF} H\mathbf{V} {RF}\mathbf{\tilde V}_D $ 的主对角线元素。同时 λ \lambda λ ∑ k = 1 K ( β k λ − q ~ k k σ 2 ) + = P \sum_{k=1}^K\left(\frac{\beta_k}{\lambda}-\tilde q_{kk}\sigma^2\right)^+=P ∑ k = 1 K ( λ β k − q ~ k k σ 2 ) + = P V ~ D \mathbf{\tilde V}_D V ~ D H e q = H V R F \mathbf{H}_{eq}=\mathbf{HV}_{RF} H e q = H V R F
整个算法收敛,应用注水功控的ZF数字预编码
V D Z F = V R F H H H ( H V R F V R F H H H ) − 1 P 1 2 = V ~ D P 1 2 \mathbf{V}_{\mathrm{D}}^{\mathrm{ZF}}=\mathbf{V}_{\mathrm{RF}}^{H} \mathbf{H}^{H}\left(\mathbf{H V}_{\mathrm{RF}} \mathbf{V}_{\mathrm{RF}}^{H} \mathbf{H}^{H}\right)^{-1} \mathbf{P}^{\frac{1}{2}}=\tilde{\mathbf{V}}_{\mathrm{D}} \mathbf{P}^{\frac{1}{2}}
V D Z F = V R F H H H ( H V R F V R F H H H ) − 1 P 2 1 = V ~ D P 2 1
\begin{aligned}
&\hline \begin{array}{l}
\text { Algorithm 3. Design of Hybrid Precoders for MU-MISO } \\
\text { systems }
\end{array} \\
&\hline \text { Given: } \beta_{k}, P, \sigma^{2} \\
&\text { 1: Start with a feasible } \mathbf{V}_{\mathrm{RF}} \text { and } \mathbf{P}=\mathbf{I}_{K} \text {. } \\
&\text { 2: for } j=1 \rightarrow N^{\mathrm{RF}} \\
&\text { 3:\quad Calculate } \mathbf{A}_{j}=\mathbf{P}^{-\frac{1}{2}} \mathbf{H} \overline{\mathbf{V}}_{\mathrm{RF}}^{j}\left(\overline{\mathbf{V}}_{\mathrm{RF}}^{j}\right)^{H} \mathbf{H}^{H} \mathbf{P}^{-\frac{1}{2}} \\
&\text { 4: } \quad \text { for } i=1 \rightarrow N \\
&\text { 5: } \quad\quad \text { Find } \zeta_{i j}^{B}, \zeta_{i j}^{D}, \eta_{i j}^{B}, \eta_{i j}^{D} \text { as defined in Appendix A. } \\
&\text { 6: } \quad\quad \text { Calculate } \theta_{i, j}^{(1)} \text { and } \theta_{i, j}^{(2)} \text { according to }(27) . \\
&\text { 7: } \quad\quad \text { Find } \theta_{i, j}^{\text {opt }}=\arg \min \left(\hat{f}\left(\theta_{i, j}^{(1)}\right), \hat{f}\left(\theta_{i, j}^{(2)}\right)\right) . \\
&\text { 8:\quad Set } \mathbf{V}_{\mathrm{RF}}(i, j)=e^{-j \theta_{i, j}^{\text {opt }}} \text {. } \\
&\text { 9: \quad end for } \\
&\text { 10: end for } \\
&\text { 11: Check convergence of RF precoder. If yes, continue; if not } \\
&\text { go to Step } 2 . \\
&\text { 12: Find } \mathbf{P}=\operatorname{diag}\left[p_{1}, \ldots, p_{k}\right] \text { using water-filling as in (23). } \\
&\text { 13: Check convergence of the overall algorithm. If yes, stop; } \\
&\text { if not go to Step } 2 . \\
&\text { 14: Set } \mathbf{V}_{\mathrm{D}}=\mathbf{V}_{\mathrm{RF}}^{H} \mathbf{H}^{H}\left(\mathbf{H V}_{\mathrm{RF}} \mathbf{V}_{\mathrm{RF}}^{H} \mathbf{H}^{H}\right)^{-1} \mathbf{P}^{\frac{1}{2}} \text {. }\\\hline
\end{aligned}
与第三篇先计算波束赋形矢量后再进行量化不同,在迭代优化过程中就开始量化 ,尤其是max R e { V R F ∗ ( i , j ) η i j } \max\ \mathrm{Re}\{\mathbf{V}_{RF}^*(i,j)\eta_{ij}\} max R e { V R F ∗ ( i , j ) η i j } V R F \mathbf{V}_{RF} V R F η i j \eta_{ij} η i j
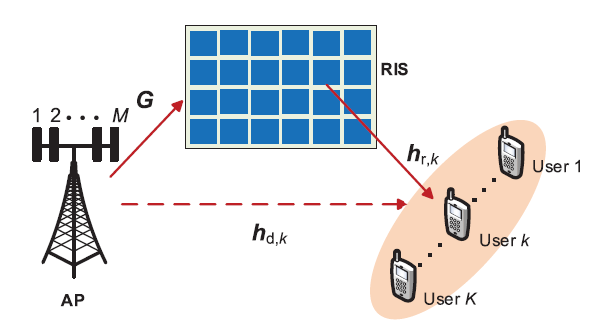
MU-MISO
基站M M M N N N K K K
y k = h d , k H x ⏟ Direct link + h r , k H Θ G x ⏟ RIS-aided link + u k = ( h d , k H + h r , k H Θ G ) ∑ k = 1 K w k s k + u k = ( h d , k H + θ H H r , k ) ∑ k = 1 K w k s k + u k \begin{aligned}
y_{k} &=\underbrace{\mathbf{h}_{\mathrm{d}, k}^{\mathrm{H}} \mathbf{x}}_{\text {Direct link }}+\underbrace{\mathbf{h}_{\mathrm{r}, k}^{\mathrm{H}} \Theta \mathbf{G} \mathbf{x}}_{\text {RIS-aided link }}+u_{k} \\
&=\left(\mathbf{h}_{\mathrm{d}, k}^{\mathrm{H}}+\mathbf{h}_{\mathrm{r}, k}^{\mathrm{H}} \Theta \mathbf{G}\right) \sum_{k=1}^{K} \mathbf{w}_{k} s_{k}+u_{k}\\
&=\left(\mathbf{h}_{d,k}^H+\boldsymbol{\theta}^H\mathbf{H}_{r,k}\right)\sum_{k=1}^K\mathbf{w}_ks_k+u_k
\end{aligned}
y k = Direct link h d , k H x + RIS-aided link h r , k H Θ G x + u k = ( h d , k H + h r , k H Θ G ) k = 1 ∑ K w k s k + u k = ( h d , k H + θ H H r , k ) k = 1 ∑ K w k s k + u k
其中,Θ = d i a g ( θ 1 , ⋯ , θ N ) , θ = [ θ 1 , ⋯ , θ N ] H \boldsymbol{\Theta}=diag(\theta_1,\cdots,\theta_N),\boldsymbol{\theta}=[\theta_1,\cdots,\theta_N]^H Θ = d i a g ( θ 1 , ⋯ , θ N ) , θ = [ θ 1 , ⋯ , θ N ] H H r , k = d i a g ( h r , k H ) G ∈ C N × M \mathbf{H}_{r,k}=diag(\mathbf{h}_{r,k}^H)\mathbf{G}\in\mathbb{C}^{N\times M} H r , k = d i a g ( h r , k H ) G ∈ C N × M
perfect CSI:weighted sum-rate maximization
max W , θ f A ( W , θ ) = ∑ k = 1 K ω k log ( 1 + γ k ) s.t. ∣ θ n ∣ = 1 , ∀ n = 1 , ⋯ , N ∑ k = 1 K ∥ w k ∥ 2 ≤ P T \begin{aligned}
\max _{\mathbf{W}, \boldsymbol{\theta}} \quad &f_{\mathrm{A}}(\mathbf{W}, \boldsymbol{\theta})=\sum_{k=1}^{K} \omega_{k} \log \left(1+\gamma_{k}\right) \\
\text { s.t. }\quad&\left|\theta_{n}\right|=1, \quad \forall n=1, \cdots, N \\
&\sum_{k=1}^{K}\left\|\mathbf{w}_{k}\right\|^{2} \leq P_{\mathrm{T}}
\end{aligned}
W , θ max s.t. f A ( W , θ ) = k = 1 ∑ K ω k log ( 1 + γ k ) ∣ θ n ∣ = 1 , ∀ n = 1 , ⋯ , N k = 1 ∑ K ∥ w k ∥ 2 ≤ P T
γ k \gamma_k γ k
imperfect CSI:$ \mathbf{h}_{d,k}$ , G \mathbf{G} G h r , k \mathbf{h}_{r,k} h r , k ( h ^ d , k ({\hat{\mathbf{h}}}_{d,k} ( h ^ d , k G ^ \hat{\mathbf{G}} G ^ h ^ r , k {\hat{\mathbf{h}}}_{r,k} h ^ r , k z d , k \mathbf{z}_{d,\ k} z d , k Z G \mathbf{Z}_G Z G z r , k \mathbf{z}_{r,k} z r , k
max θ f B ( θ ) = E ξ [ max W ξ f A ( W ( ξ ) , θ ; ξ ) ] s.t. ∣ θ n ∣ = 1 , ∀ n = 1 , ⋯ , N ∑ k = 1 K ∥ w k ( ξ ) ∥ 2 ≤ P T , ∀ ξ . \begin{aligned}
\max _{ \boldsymbol{\theta}} \quad &f_{\mathrm{B}}(\boldsymbol{\theta})=\mathbb{E}_\xi\left[\max_{\mathbf{W}_\xi}f_A\left(\mathbf{W}(\xi) ,\boldsymbol{\theta};\xi \right)\right] \\
\text { s.t. }\quad&\left|\theta_{n}\right|=1, \quad \forall n=1, \cdots, N \\
&\sum_{k=1}^{K}\left\|\mathbf{w}_{k}(\xi)\right\|^{2} \leq P_{\mathrm{T}},\quad\forall\xi.
\end{aligned}
θ max s.t. f B ( θ ) = E ξ [ W ξ max f A ( W ( ξ ) , θ ; ξ ) ] ∣ θ n ∣ = 1 , ∀ n = 1 , ⋯ , N k = 1 ∑ K ∥ w k ( ξ ) ∥ 2 ≤ P T , ∀ ξ .