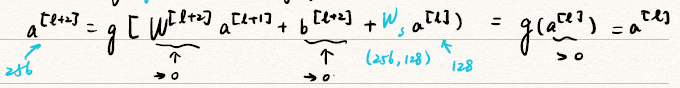/ 科研向  

【深度学习笔记（四）】卷积神经网络

这个专项课程一共五门，包括

最近在做图像大作业和各种课内作业，比较忙，搁置几天在更新。

Convolution Neural Networks 学习笔记

第四门课的主体框架

  • Week 1: Foundations of Convolutional Neural Networks
    • Convolution NN
  • Week 2: Deep Convolutional Models: Case Studies
    • Case Studies
    • Practical advices for using ConvNets
  • Week 3: Object Detection
    • Detection algorithm
  • Week 4: Special Applications: Face recognition & Neural Style Transfer
    • Face Recognition
    • Neural Style transfer

待更新

Week 1: Foundations of Convolutional Neural Networks

图像处理基础知识

Computer Vision

  • Computer Vision
    • brand new applications
    • create a lot of cross_fertilization into other areas
  • CV problems——photos are large
    • Image classification
    • Object detection
    • Neural Style Transfer

Edge detection Example

在传统的图像分析中，我们可以利用模板卷积的方式实现图像的平滑，锐化，边缘检测等操作。这里就以垂直、水平边缘检测为例介绍了模板卷积的基本操作。

在使用模板卷积进行边缘检测时，我们一般先检测垂直线条，再检测水平线条。

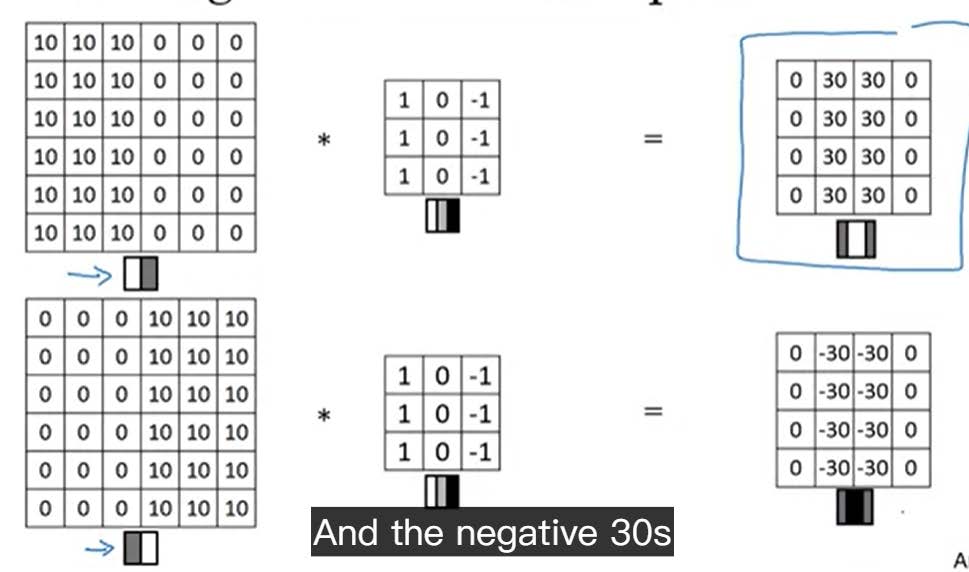
  • 垂直边缘检测：
    垂直边缘检测

    • 这里的卷积就是将模板滤波器（filter）在实际的图片上拖动，并且相乘相加。

    • 比较这里的卷积（convolution）和信号与系统中的卷积运算，其实是将一维卷积拓展到了二维，但少了翻转（slips）这一步骤，故在图像处理中的卷积运算其实是相关（correlation）运算，但因为约定俗成的名称，我们将他叫做卷积。

    • 二维的卷积在各种编程语言中可以用简单的命令实现。

      1
      2
      3
      conv-forward()	 # python
      tf.nn.conv2d()	 # tensorflow
      Conv2D()		# keras
      1
      conv2()			# matlab

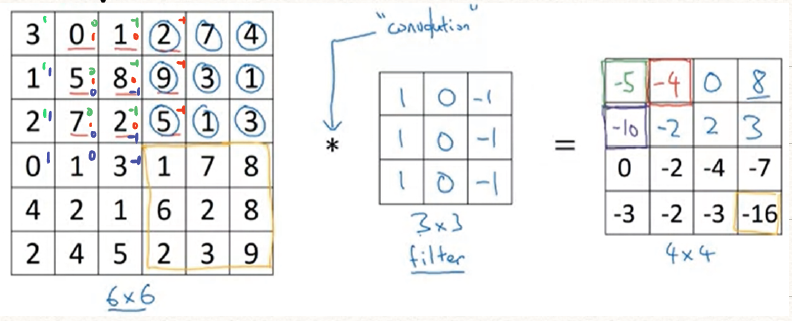
    • 举个垂直边缘检测的例子
      垂直边缘检测例子
      可以发现他利用3×33\times 3的卷积模板[10−110−110−1]\begin{bmatrix}1&0&-1\\1&0&-1\\1&0&-1\end{bmatrix}检测出了垂直线条，他的原理其实是利用图像边缘是一阶导数的极值点，利用梯度算子来检测边缘。

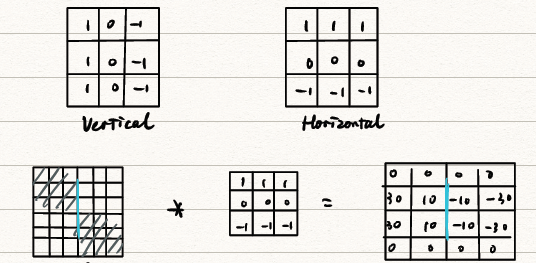
  • 垂直边缘检测模板和水平边缘检测模板

    • 垂直边缘检测模板：[10−110−110−1]\begin{bmatrix}1&0&-1\\1&0&-1\\1&0&-1\end{bmatrix}
    • 水平边缘检测模板：[111000−1−1−1]\begin{bmatrix}1&1&1\\0&0&0\\-1&-1&-1\end{bmatrix}
    • 水平边缘检测模板例子
      水平边缘检测例子

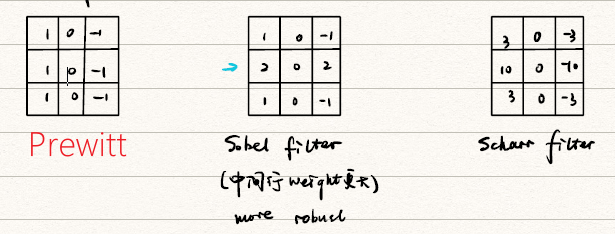
  • 更多种类的边缘检测模板
    边缘检测模板
    注意到这些检测模板都只能检测水平或者是垂直的线条，当然也有利用平均差分方向梯度、十二方向梯度等方式检测斜线，但显然还是很复杂。下面我们将谈到如何解决这个问题。

  • 传统图像分析的平滑、锐化、边缘检测模板类型特点（来自《现代图像分析》幻灯片）
    传统模板

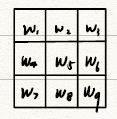
  • 深度学习——让神经网络自己训练学习3×33\times3卷积模板中的9个参数
    深度学习
    为了让能检测各种方向的线条，利用图像卷积实现更多的效果，我们可以通过深度学习来训练这个卷积模板，当然他不一定是3×33\times 3的，可以是5×55\times 5甚至更高维度的。一般我们选择奇数维的卷积模板。

CNN基本组件

在本节中，我们介绍卷积的基本操作方式和CNN的常见组件，是他的的有序结合得到了CNN。

Padding

注意到上面的例子中，我们对一个6×66\times 6的图像利用3×33\times3的模板进行卷积，得到了4×44\times 4的结果。推而广之，对一个n×nn\times n的图像利用f×ff\times f的模板进行卷积，将得到了(n−f+1)×(n−f+1)(n-f+1)\times (n-f+1)的结果。可以发现：

  • 矩阵的维数变少了（shrinking output）
  • 注意到在角落和边缘的数据信息没有被充分利用

解决上述两个问题的方法就是——Padding

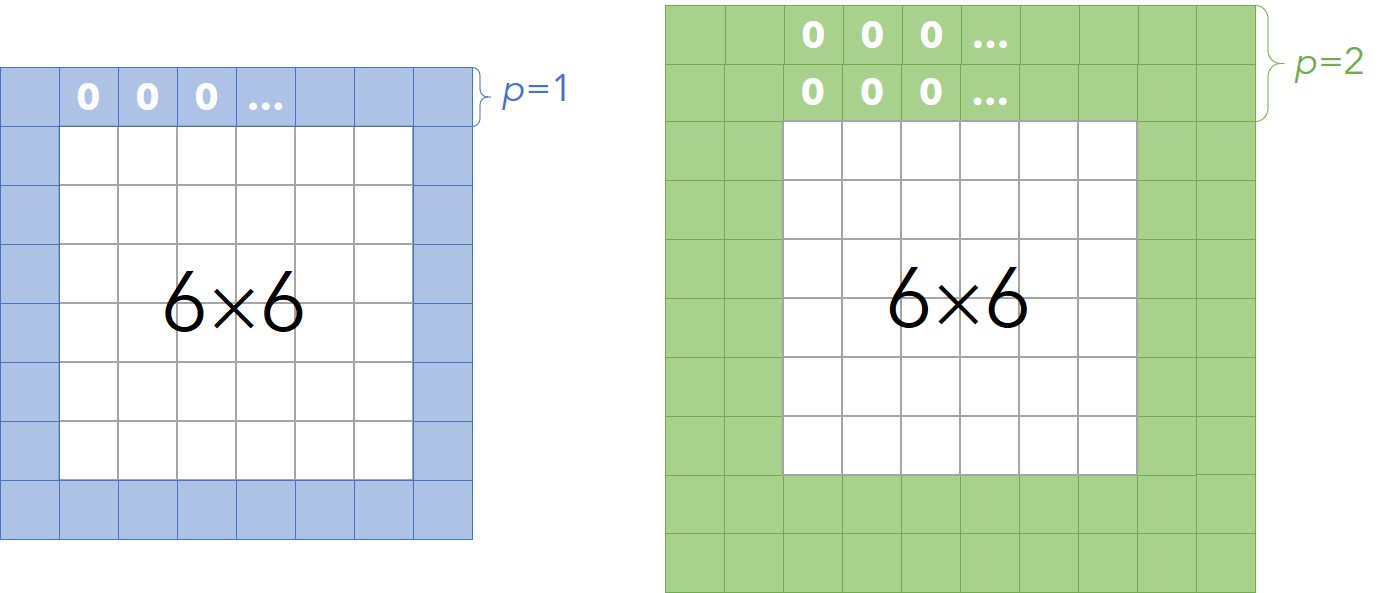
padding

对6×66\times6的图像用0加一圈边就变成了8×88\times 8的图像，再用3×33\times 3的模板进行卷积得到的结果就是6×66\times6的了，此时图片的维度没有发生变化。我们把这种情况记作p=1p=1。推而广之，对一个n×nn\times n的图像，进行pp-Padding，利用f×ff\times f的模板进行卷积，将得到了(n+2p−f+1)×(n+2p−f+1)(n+2p-f+1)\times (n+2p-f+1)的结果。

Padding的两种极端是：

  • Valid Convolution：有效卷积，即我们进行卷积的都是有效数据，这种情况就退化到了最一般的二维卷积

    n×n∗f×f=(n−f+1)×(n−f+1)\begin{aligned} n\times n &*&f\times f&=(n-f+1)\times (n-f+1) \end{aligned}

  • Same Convolution：相同卷积，即保持我们卷积输出结果和输入矩阵维数一致。

    (n+2p)×(n+2p)∗f×f=(n+2p−f+1)×(n+2p−f+1)\begin{aligned} (n+2p)\times (n+2p) &*&f\times f&=(n+2p-f+1)\times (n+2p-f+1) \end{aligned}

    若保持输出与输入维数一致，则n+2p−f+1=nn+2p-f+1=n，即p=f−12p=\frac{f-1}{2}。

Strided convolution

在进行卷积操作时，我们有时也需要压缩矩阵的维数，以获得一个更小的矩阵，我们可以通过卷积模板两次移动之间的跨越方格数来调整，而这就被称为stride。

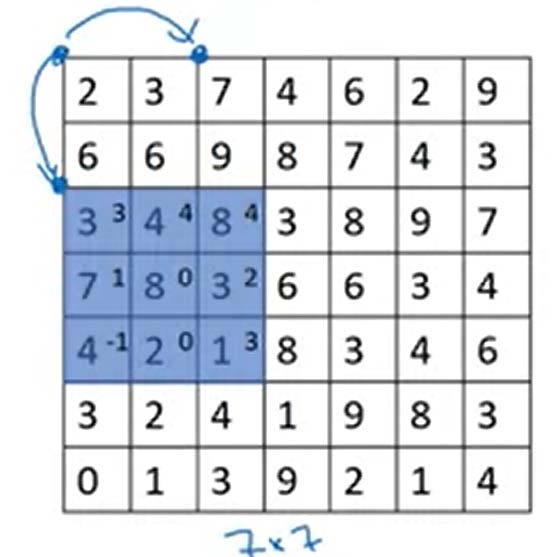
stride

上图蓝色点的移动跨度ss为2，对应于卷积模板的左上角点。对于一个7×77\times 7的图像，以s=2s=2为跨度用3×33\times 3的模板进行卷积，得到的结果图像是3×33\times 3维的。更一般的可以写成

n×n∗f×f=⌊n+2p−fs+1⌋×⌊n+2p−fs+1⌋\begin{aligned} n\times n &*&f\times f&=\left\lfloor\frac{n+2p-f}{s}+1\right\rfloor\times\left\lfloor\frac{n+2p-f}{s}+1\right\rfloor \end{aligned}

Convolutions Over Volume

卷积不光可以对二维的图像进行，还可以对有多个维度的图像进行，比如对RGB三个通道的灰度图像分别进行卷积。
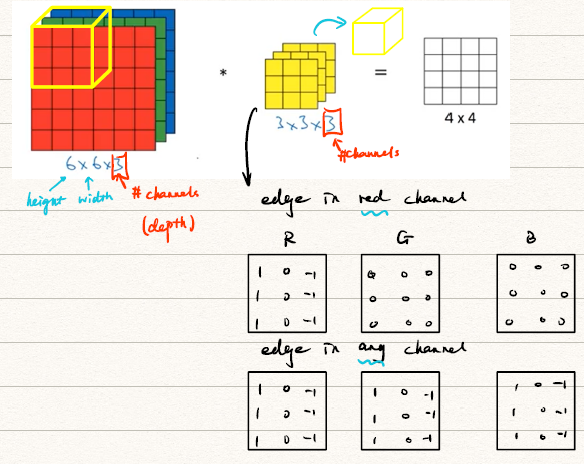
Volume

注意到图片的前两个维度表示长和宽，第三个维度表示通道数（number of channel，也被叫做深度，depth）。对于存在通道数的卷积其实和二维卷积类似，我们计算每个通道上的卷积，再将对应点相加即可得到在Volume进行的卷积结果。值得注意的是，对于多通道的图像利用有多通道的卷积模板进行卷积最后得到的是一个二维图像。

那么如何得到有多个通道的图像呢？——我们需要利用多个卷积模板滤波器

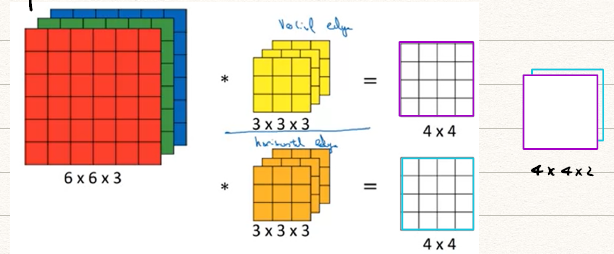
Volume_2

我们对多通道的图像利用NN次多通道的卷积模板进行卷积即可得到NN个通道的图像，比如我们对RGB三通道图像施加一个垂直边缘检测模板，一个水平边缘检测模板，即可得到一个两通道的图像含有水平和平行边缘的信息。

Pooling Layers

Pooling实际上和卷积操作机理并不相同，但是他也是CNN中常用的组件。Pooling主要有两种方式：Max pooling和Average pooling。

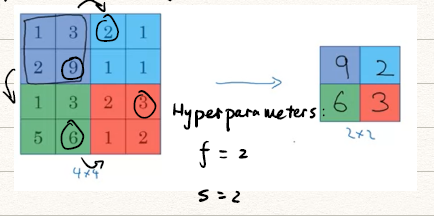
  • Max pooling：移动模板，取每次被框选的数据中最大的一个（注意这里不再需要卷积，也就不需要模板的数值了）
    • 对一个4×44\times 4的图像，使用2×22\times 2的模板以stride=2stride=2为跨度，每次取框选数值中的最大值得到右图的数值。
      pooling
    • 换言之，如果这些特征在这个filter中被检测到，那么保持一个高的数字。这样可以显著的降低矩阵的维数。
    • 但是对于有多个通道的图像，我们需要注意pooling仅是针对一个维度而言的，这个卷积的操作并不一样。
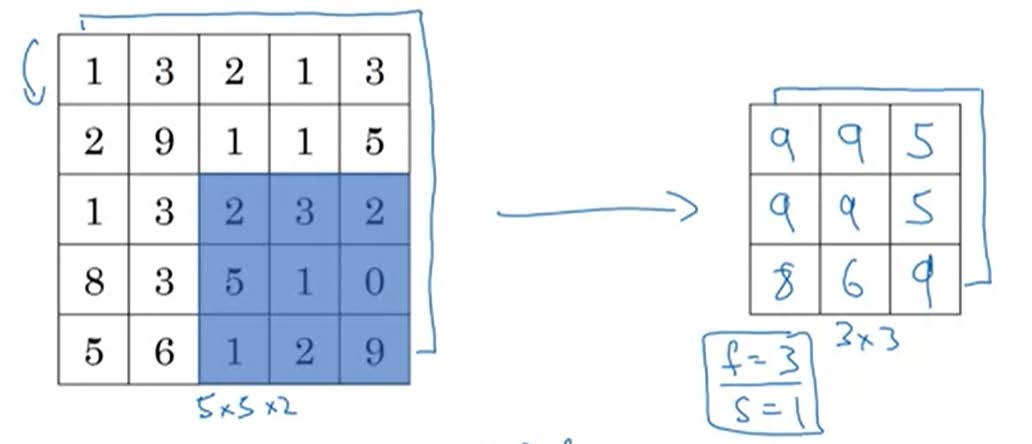
      pooling_channel
      如上图对于一个5×5×25\times 5\times 2的图像，使用3×33\times 3的模板以s=1s=1为跨度进行Max Pooling得到的结果是一个3×3×23\times 3\times 2的图像。
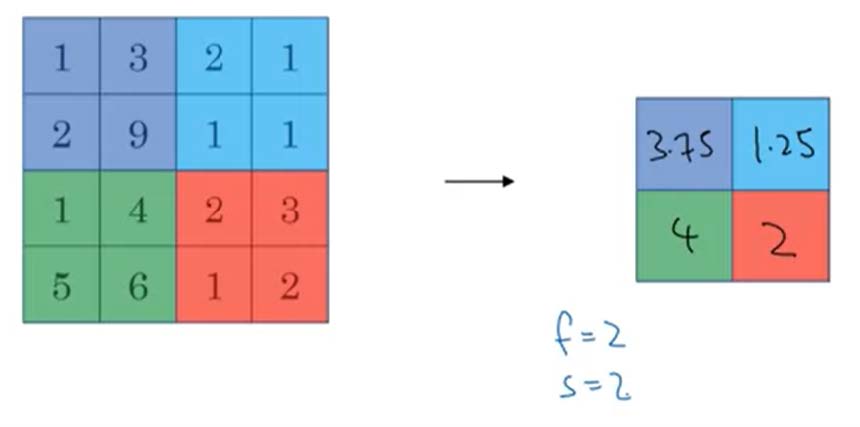
  • Average Pooling：和Max pooling不同的是，此时所取得值为被框选数值得平均值。
    • pooling_3
    • Average Pooling的主要用途为在深度很深的NN中，⽤均值采样合并表示

小小总结以下，在Padding操作中，只存在超参数(ff for filfter size, ss for stride)，不需要Padding。不论是对于Max Pooling还是Average Pooling都没有参数需要学习。经过Pooling后矩阵的维数变为

nH×nW×nC→⌊n−fs+1⌋×⌊n−fs+1⌋\begin{aligned} n_H\times n_W \times n_C\to\left\lfloor\frac{n-f}{s}+1\right\rfloor\times\left\lfloor\frac{n-f}{s}+1\right\rfloor \end{aligned}

构建CNN

下面，利用上面学习到的卷积的基本操作和CNN组件来一步一步搭建CNN。

One layer of CNN

首先考虑对于单层的CNN的搭建。

卷积实际上是一个线性的过程，我们显然需要非线性函数使他变成一个标准的NN，比如ReLU。
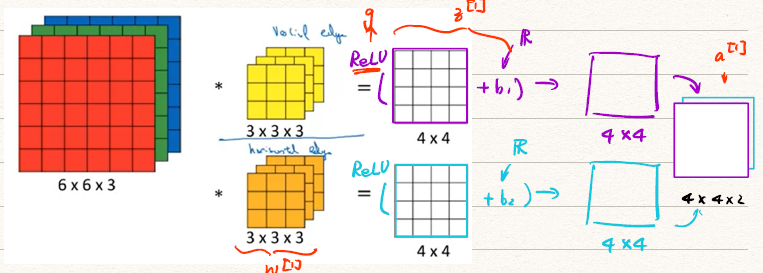
one_layer

那么我们可以把这个前向传播过程表述为

z[1]=w[1]a[0]+b[1]a[1]=g(z[1])\begin{gathered} z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}\\ a^{[1]}=g(z^{[1]}) \end{gathered}

上图可以简单表示为
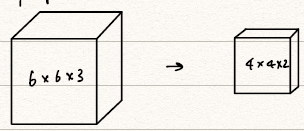
one_layer

  • 在一层CNN中参数的个数
    例如，对于利用3×3×33\times 3\times 3的卷积模板作卷积需要(3×3×3+bias)=28(3\times 3\times 3+bias)=28个参数，如果产生的通道数为10，则需要10个这样的模板，即需要28×10=28028\times 10=280个参数。

  • Notation：
    If layer ll is a convolution layer.

    • Input: nH[l−1]×nW[l−1]×nc[l−1]n_{H}^{[ l-1]} \times n_{W}^{[l-1]} \times n_{c}^{[l-1]}
      Output: nH[l]×nW[l]×nc[l]n_{H}^{[ l]} \times n_{W}^{[l]} \times n_{c}^{[l]}（其中，n∙[l]=⌊n∙[l−1]+2p[l]−f[l]s[l]+1⌋n_{\bullet}^{[l]}=\left\lfloor\frac{n_{\bullet}^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor,∙=H or W\bullet=H\text{ or }W）
      • f[l]f^{[l]}: filter size of lthl^{th} layer
      • p[l]p^{[l]}: padding
      • s[l]s^{[l]}: stride
      • nc[l]n_c^{[l]}: number of filters
    • Each filter is f[l]×f[l]×nc[l−1]f^{[l]}\times f^{[l]}\times n_c^{[l-1]}
    • Activation: a[l]→nH[l]×nW[l]×nc[l],A[l]→m×nH[l]×nW[l]×nc[l]a^{[l]}\to n_{H}^{[ l]} \times n_{W}^{[l]} \times n_{c}^{[l]},\quad A^{[l]}\to m\times n_{H}^{[ l]} \times n_{W}^{[l]} \times n_{c}^{[l]}
    • Weight: f[l]×f[l]×nc[l−1]×nc[l]f^{[l]}\times f^{[l]}\times n_{c}^{[ l-1]} \times n_{c}^{[l]}
    • Bias: nc[l]→1×1×1×nc[l]n_{c}^{[l]}\to 1\times 1\times 1\times n_c^{[l]}

Simple Convolutional Network example

对于一个简单的卷积网络（ConvNet），我们可以用单层CNN组装而成
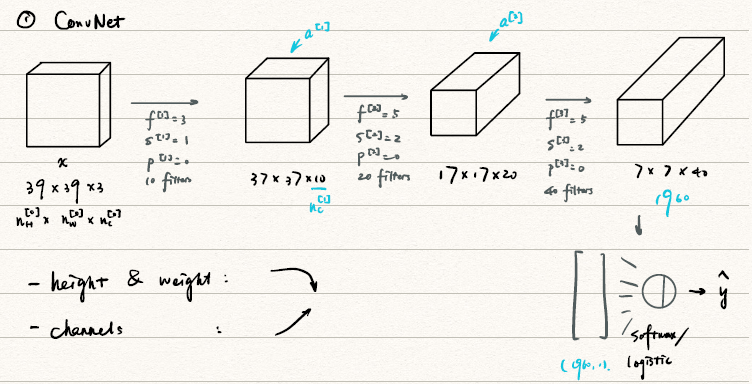
SImple

CNN网络中常见的组件：

  • CONV: Convolution
  • POOL：Pooling
  • FC：Fully Connected

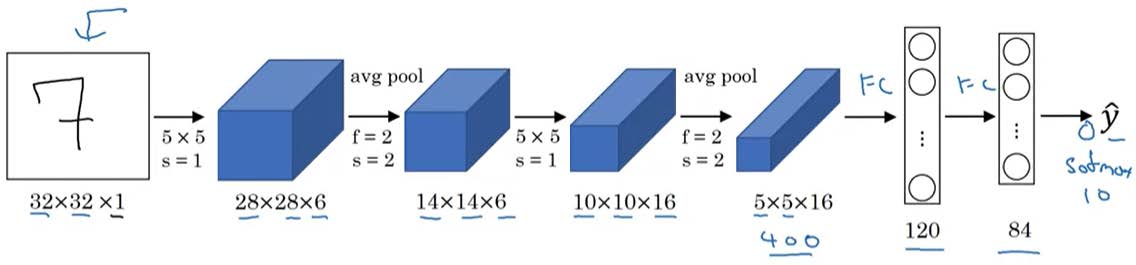
CNN example

下图是一个使用LeNet-5实现手写数字识别的过程。

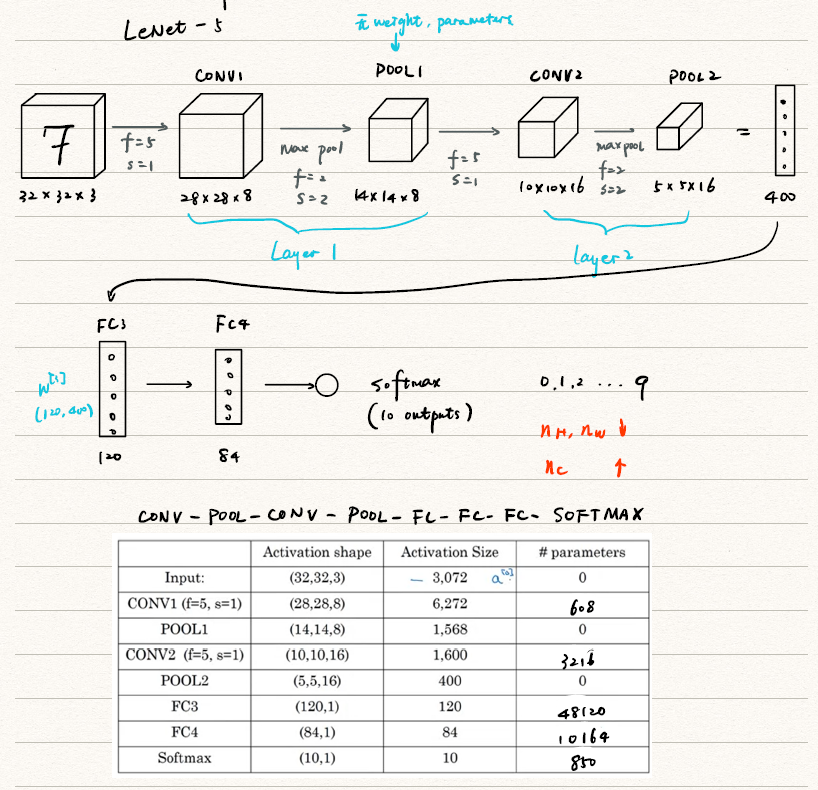
LeNet-5

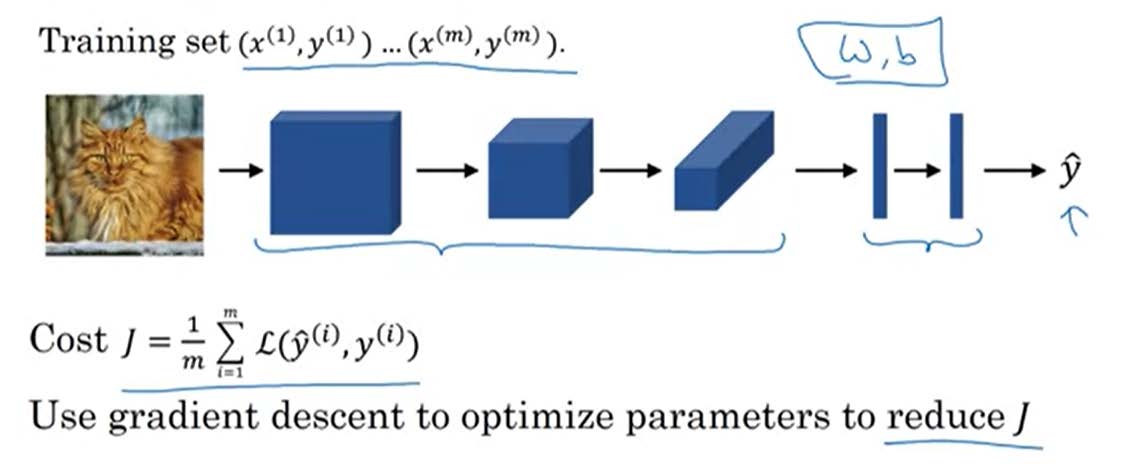
Why convolution？

相对于前面三门课程的DNN，为何对于图像要使用CNN呢？

  • parameter sharing 参数共享：可以减少parameters 的个数
  • sparsity of connection 稀疏性： each output value depends only a small number ofinputs
  • put it together
    Why?

Week 2：Deep Convolutional Models: Case Studies

Case Studies

本节中主要介绍一些常用的CNN模型，包括传统模型、ResNet和Inception Network.

Classic Networks

  1. LeNet-5(1998年)
    LeNet-5

    网络特点：

    • 60k parameters（比较小）
    • 随着网络的深入，nH,nW↓, nc↑n_H,n_W\downarrow,\ n_c\uparrow
    • 网络结构：CONV→POOL→CONV→POOL→FC→FC→Output
    • 由于提出时间比较早，使用的主要是sigmoid/tanh，而不是现在比较流行的ReLU

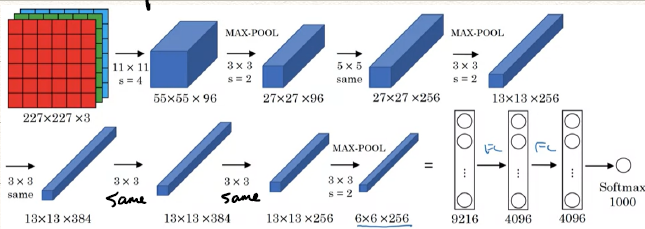
  2. AlexNect（2012年）
    AlexNet

    网络特点：

    • 有更多的参数，达到了60 M。
    • 使用性能更好的ReLU函数，而非sigmoid或是tanh。
    • 但是文章中的多GPU是现在不需要考虑的，Local response Normalization （LRN）是吴恩达不推荐的，Andrew Ng认为他没有必要

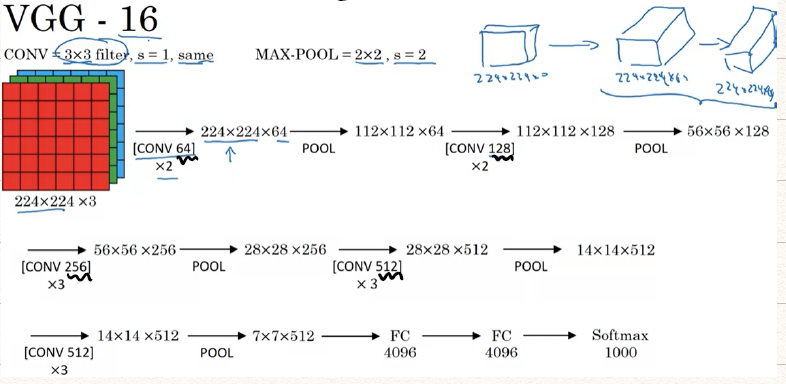
  3. VGG-16

    网络最突出的特点就是所有CONV层和POOL层采用的都是一样的参数

    • CONV: 采用3×33\times 3 filters，s=1s=1，same
    • MAX-POOL：采用2×22\times 2 filters, s=2s=2

    VGG-16

    • 该网络有128 M的参数
    • 除此以外还有VGG-19

ResNet (Residual Networks)

gradient vanishing/exploding → skip connection → ResNet（残差⽹络）

为了抑制梯度消失或者梯度爆炸，我们采取跳过几层网络直接作用的方式，这就构成了残差网络。

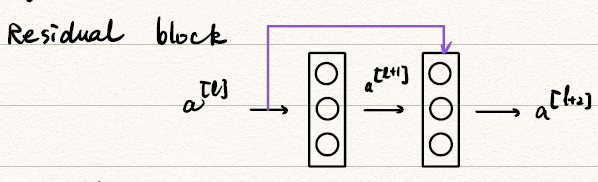
  1. Residual block
    block

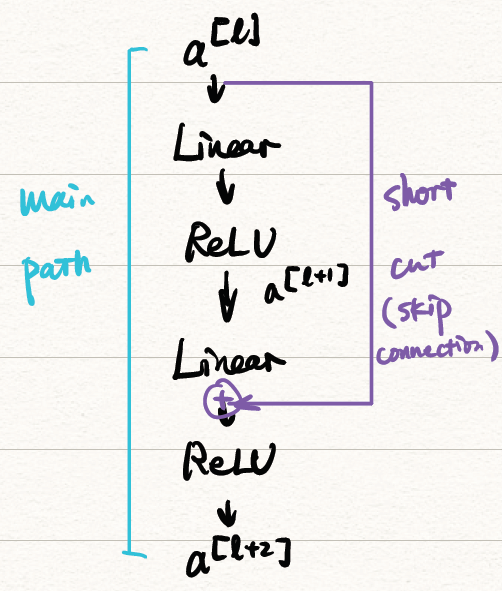
    更细致的可以画成这样：

    path

    将Residual block用数学公式表达：

    z[l+1]=W[l+1]a[l]+b[l+1]a[l+1]=g(z[l+1])z[l+2]=W[l+1]a[l+1]+b[l+2]a[l+2]=g(z[l+2])a[l+2]=g(z[l+2]+a[l])\begin{aligned} z^{[l+1]}=&W^{[l+1]}a^{[l]}+b^{[l+1]}\\ a^{[l+1]}=&g(z^{[l+1]})\\ z^{[l+2]}=&W^{[l+1]}a^{[l+1]}+b^{[l+2]}\\ a^{[l+2]}=&g(z^{[l+2]})\\ \boldsymbol{a^{[l+2]}=}&\boldsymbol{g(z^{[l+2]}+a^{[l]})} \end{aligned}

  2. Residual Network

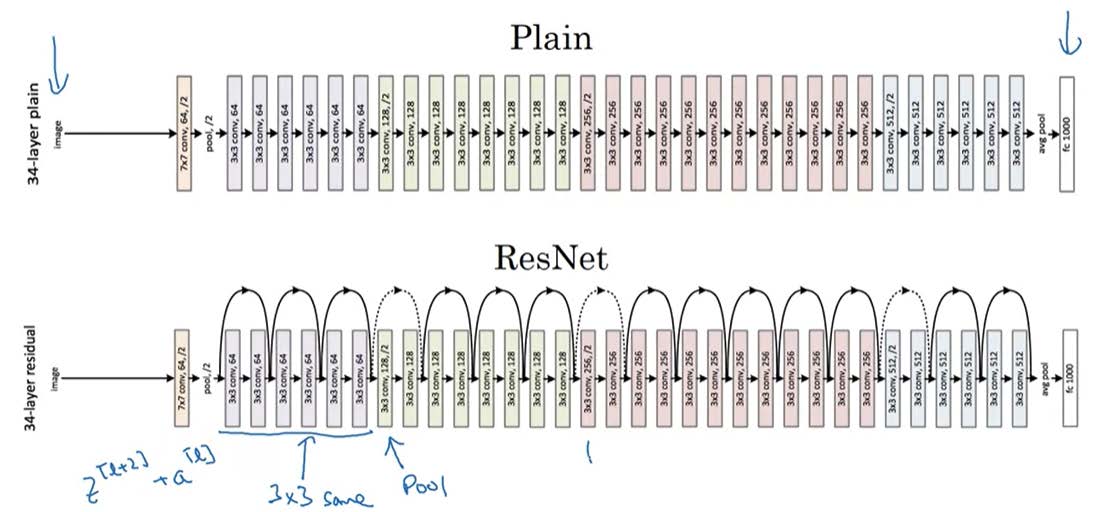
    • 我们Residual block级联，就可以构成一个最简单的ResNet。其中黑色的是plain network，加上了skip connection后它就变成了ResNet
      ResNet_plain

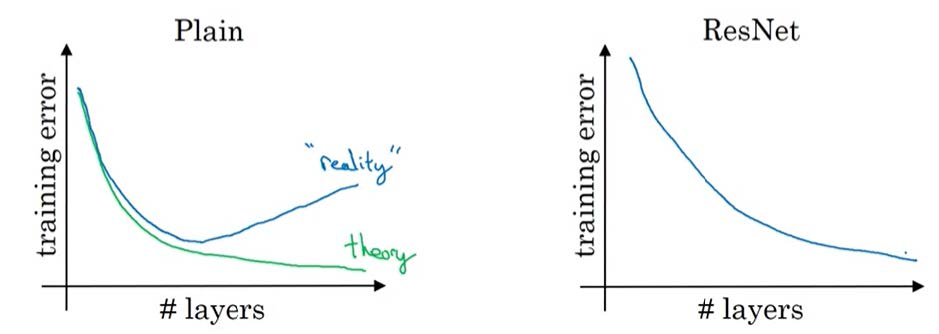
    • 对比普通网络和ResNet的性能

      compare 可以发现一般的网络在网络层数增加到一定多时，错误率不降反升，这是因为前后参数之间没有建立起联系，而ResNet通过跳跃的方式是的前后之间有所牵制，不至于梯度消失或爆炸。

    • 为什么ResNet能够运行起来呢？

      • The identity function（恒等函数） is easy for residual block to learn.
        identity function
      • Adding residual block doesnt hurt NN only
      • help performance——底线是不会破坏网络，可能会出奇效
        • baseline: not hurt NN
        • help: gradient descent mayhelp improve

    ResNet

Inception Network

  1. Networks in Networks and 1×11\times 1 convolution

Practical advices for using ConvNets

Transfer learning

Data Augmentation

State of CV

Week 3: Object Detection

目标识别基础

Object localization

Landmark Detection

目标识别组件

Object detection

Convolutional Implementation of Sliding Windows

Bounding Box Algorithm

Make YOLO Better

应用YOLO

YOLO Algorithm

Region Proposals

Week 4: Special Applications: Face recognition & Neural Style Transfer

Face Recognition

What is face recognition？

One-shot learning

Siamese Network

triplet loss

Face verification and Binary classification

Neural Style transfer

❗Alert: 该浏览器不支持PDF。请点击下载查看: Download PDF.

该beamer建议在支持动画的PDF阅读器上播放。比如Adobe Acrobat DC等，否则无法播放动画哦。

本文标题:【深度学习笔记（四）】卷积神经网络

文章作者:Levitate_

发布时间:2021年05月06日 - 20:01:14

原始链接:https://levitate-qian.github.io/2021/05/07/DL-Coursera-4-Convolutional-Neural-Networks/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。