/ 实验  

【B测】数字2DPSK频带传输系统的设计

数字2DPSK频带传输系统的设计

以下是我们B测题的大致思路。

作者：钱辰涞、许琛、刘育涵

一、任务要求

任务

编程语言不限（推荐使用LabVIEW软件，其他编程语言，如Matlab、C等也可），对一数字频带传输系统进行调制与解调设计，输入输出时域波形和频域波形等，数字频带传输系统为2DPSK。

要求

  1. 码率：24kbit/s；

  2. 获取时域波形和频域波形；

  3. 完成实验报告。

说明

  1. 信道采用高斯信道；
  2. 解调采用相干解调；
  3. 要求波形正确、清晰，便于分析；
  4. 报告要对数据、波形进行分析、说明，获取信息，得出合理、正确结论。

二、仿真环境

  • OS环境：Windows 10
  • 处理器类型：x86_64
  • 软件名称：Matlab
  • Matlab版本：R2020a (9.8.0.1323502)

三、实现原理与方案

2DPSK信号的调制与解调原理

传输系统中要保证信息的有效传输就必须要有较高的传输速率和较低的误码率，为实现低误码率，传输信号本身的误码率应控制在一定的范围内。在传输信号中，2PSK 信号和2ASK 及2FSK 信号相比，具有较好的误码率性能。但是，在2PSK信号传输系统中 存在载波相位模糊，会造成倒π\pi工作（反相工作），恢复出的数字信号"1"和"0"倒置，故2PSK难以应用。为克服此缺点，提出了二进制差分相移键控(2DPSK)方式。

2DPSK信号的产生原理

2DPSK信号利用前后相邻码元的载波相对相位变化传递数字信息。于是可以将一组二进制数字信息与其对应的2DPSK信号的载波相位关系示意如下[^1]：

二进制数字信息 1 1 0 1 0 0 1 1 0 1 0 1
2DPSK信号相位 (0) π\pi 0 0 π\pi π\pi π\pi 0 π\pi π\pi 0 0 π\pi

2DPSK信号产生的原理为：

  1. 对二进制数字基带信号进行差分编码，获得a(t)a(t)，即把数字信息序列的绝对码变为相对码；

  2. 根据相对码，对其进行绝对调相，产生二进制差分相移键控(2DPSK)信号b(t)b(t)。

差分编码中，相对码可取传号差分或空号差分。这里取传号差分码，其编码规则为

an=sn⊕an−1a_n=s_n\oplus a_{n-1}

其中：sns_n是绝对码，ana_n是相对码。使用相对码对应基带信号a(t)a(t)实现2DPSK。

2DPSK信号的解调原理

2DPSK信号的解调方式主要有两种：

  • 相干解调（极性比较法）加码变换法

  • 差分相干解调（相位比较法）

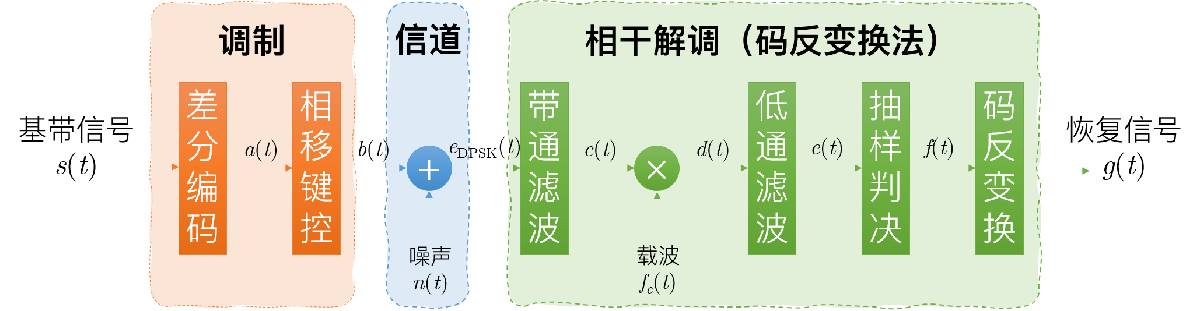
在本文中，我们使用"相干解调（极性比较法）加码变换法"，故仅对此进行一定说明。其解调原理是：

  1. 对2DPSK信号进行相干解调，恢复出相对码；

    1. 带通滤波滤除噪声，获得c(t)c(t)；

    2. 与相干载波相乘，将码元间的相位不同转变为极性不同，得到d(t)d(t)；

    3. 低通滤波滤除载波信号，获得e(t)e(t)；

    4. 经抽样、判决后将码元再生，恢复出相对码数字信息f(t)f(t)。

  2. 经码反变换器变换为绝对码，从而恢复出发送的二进制数字信息g(t)g(t)。

在解调过程中，由于载波相位模糊性的影响，使得解调出的相对码也可能是"1"和"0"倒置，但经差分译码（码反变换）得到的绝对码不会发生任何倒置的现象，从而解决了载波相位模糊性带来的问题。

总体工作流程图

总结上述2DPSK调制与解调的原理，结合高斯信道，可以画出如图的流程图，上述提到的各点的信号均标注在图上。

总体工作原理层级图

四、设计过程与仿真结果

下面从基带信号的产生、2DPSK 信号的产生、高斯信道、2DPSK 信号的相关解调四部分，对上述图2 中的各模块的代码和波形进行分析。

基带信号的产生

数据初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
clear; clc;
fs = 4.8e6;             % 设置采样频率
TB = 1/24000;           % 传送一个码元所需要的时间
Ns = fs * TB;           % 每个码元的抽样次数
HL = ones (1, Ns);      % 设置码元信号高电平
LL = zeros(1, Ns);      % 设置码元信号低电平
fc = 1e6;               % 设置载波信号频率
Signal_absolute = [1,1,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,0,1,1,0,1,1,1];    % 设定初始输入信号（绝对码）
% L_rand = 12;
% Signal_absolute = randi(2,1,L_rand) - ones(1,L_rand);
L = length (Signal_absolute);                   % 信号长度
Signal_relative = zeros(1,L);                   % 初始化相对码
st = zeros (1, Ns * L);                         % 基带信号（绝对码）
at = zeros (1, Ns * L);                         % 基带信号（相对码）
bt = zeros (1, Ns * L);                         % 基带信号调制后信号
ft = zeros (1, Ns * L);
gt = zeros (1, Ns * L);
t = 0 : 1/fs : TB * L - 1/fs;                   % 总时间
Nfft = 4800;                                    % FFT点数
k = 0 : Nfft-1;
f = round(k / Nfft * fs);                       % FFT采样频率

基带信号的产生

下面将输入离散序列扩展为时域信号，码率为 24 kbit/s。

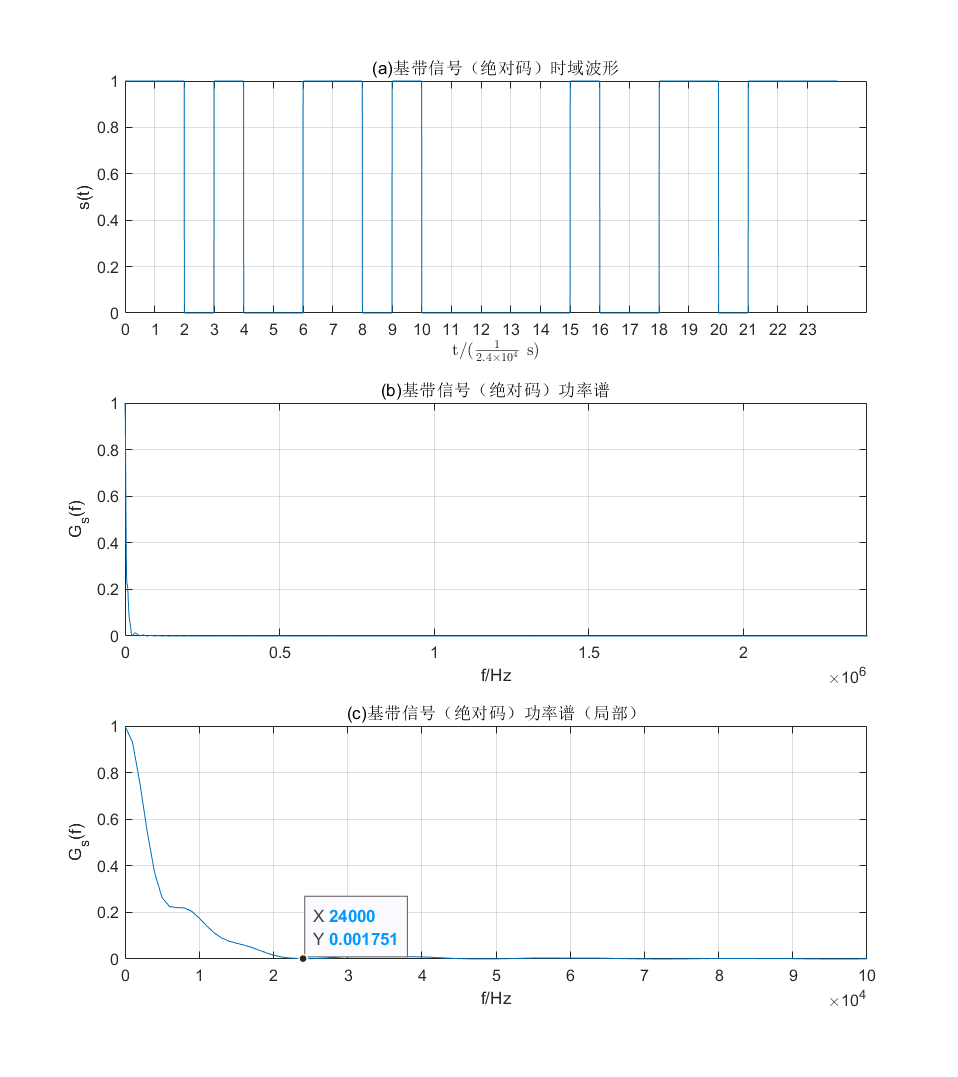
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
for i = 1 : L
    if Signal_absolute(i) == 1
        st((i-1)*Ns + 1 : i*Ns) = HL;
    else
        st((i-1)*Ns + 1 : i*Ns) = LL;
    end
end

Gs =cpsd(st,st,[],[],Nfft,fs,'twosided');

figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot(t/TB, st);
set(gca,'XTick',0:1:max(t/TB));
title ('(a)基带信号（绝对码）时域波形');
xlabel('t/($\frac{1}{2.4 \times 10^4}$ s)',"Interpreter","latex");
ylabel('s(t)');
grid
subplot(3,1,2);
plot(f,abs(Gs)/max(abs(Gs)));
set(gca,'xlim',[0,2.4e6]);
title('(b)基带信号（绝对码）功率谱');
xlabel('f/Hz');
ylabel('G_s(f)');
grid
subplot(3,1,3);
plot(f,abs(Gs)/max(abs(Gs)));
set(gca,'xlim',[0,0.1e6]);
title('(c)基带信号（绝对码）功率谱（局部）');
xlabel('f/Hz');
ylabel('G_s(f)');
ax = gca;
chart = ax.Children(1);
n = find(f==24000);
datatip(chart,f(n),Gs(n));
grid

image

观察图(a) 波形可以发现，基带信号（绝对码）符合输入序列 [1,1,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,0,1,1,0,1,1,1] 的分布特点。值得注意的是为了方便观察，这里的横坐标的最小分度取的是12.4×104\frac{1}{2.4\times 10^4 } s，对应每个码元长度，体现出了码率为 24 kbit/s。图(b,c) 是基带信号（绝对码）的功率谱密度，以下不特别说明将功率谱进行了归一化。观察图(b,c) 中的功率谱 可以发现，基带信号主要为直流分量，频率较低，因此功率谱主要集中在低频 部分。同时，带宽为B=fB=1TB=2.4×104B=f_B =\frac{1}{T_B }=2.4\times 10^4 Hz，与单极性非归零码的性质一致。由于FFT的周期性和对称性，对于4.8 MHz的采样频率我们仅取[0 Hz,2.4 MHz][0~\textrm{Hz},2.4~\textrm{MHz}] 部分的功率谱（如图(b)）。

2DPSK调制

差分编码

下面对绝对码进行差分编码，假设参考相位为0，若第一个码元为0则不变，为1则便为1，即π\pi。

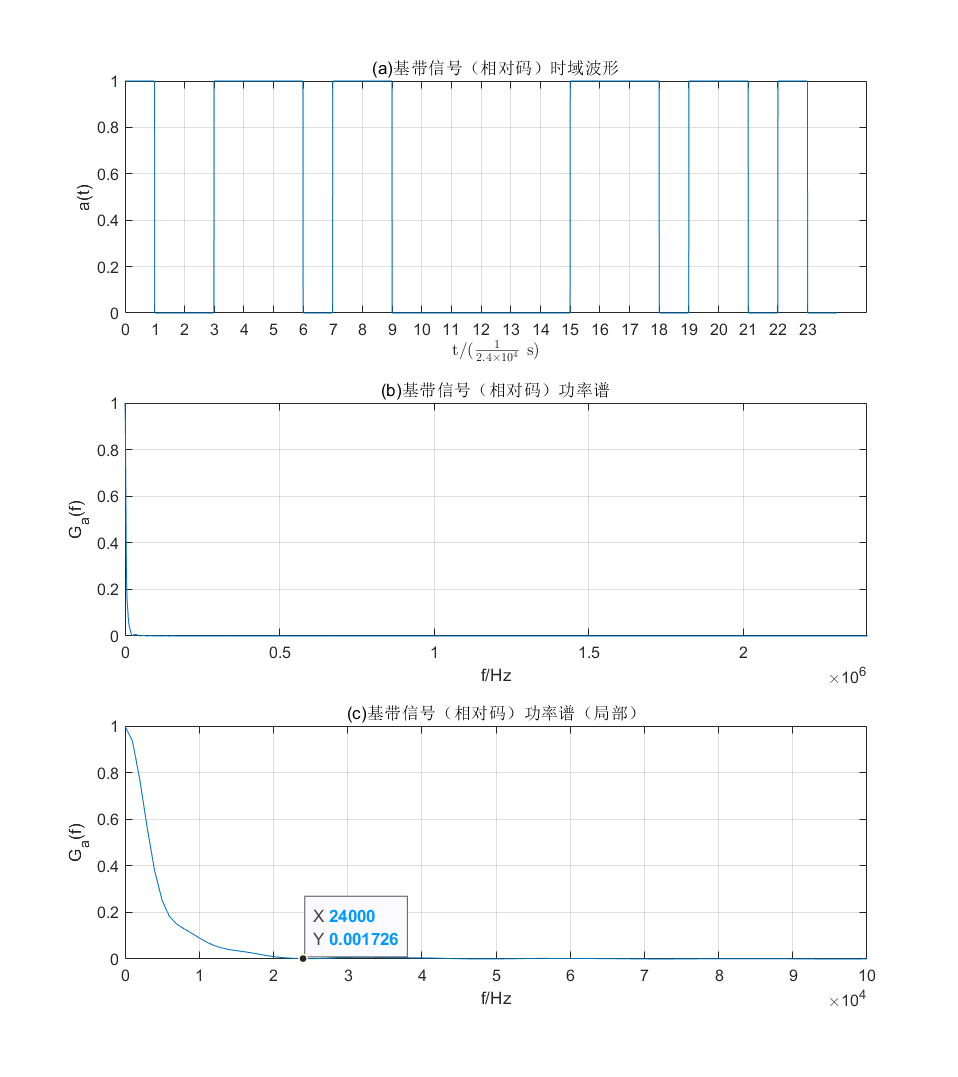
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
for i = 1 : L
    if (i == 1)
        if (Signal_absolute(1) == 0)
            Signal_relative(1) = 0;
            at(1:Ns) = LL;
        else
            Signal_relative(1) = 1;
            at(1:Ns) = HL;
        end
    elseif (Signal_absolute(i) == at((i-1)*Ns - 1))
        Signal_relative(i) = 0;
        at((i-1)*Ns + 1 : i*Ns) = LL;
    else
        Signal_relative(i) = 1;
        at((i-1)*Ns + 1 : i*Ns) = HL;
    end
end

Ga = cpsd(at,at,[],[],Nfft,fs,'twosided');

figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot(t/TB, at);
set(gca,'XTick',0:1:max(t/TB));
title ('(a)基带信号（相对码）时域波形');
xlabel('t/($\frac{1}{2.4 \times 10^4}$ s)',"Interpreter","latex");
ylabel('a(t)');
grid
subplot(3,1,2);
plot(f,abs(Ga)/max(abs(Ga)));
set(gca,'xlim',[0,2.4e6]);
title('(b)基带信号（相对码）功率谱');
xlabel('f/Hz');
ylabel('G_a(f)');
grid
subplot(3,1,3);
plot(f,abs(Ga)/max(abs(Ga)));
set(gca,'xlim',[0,0.1e6]);
title('(c)基带信号（相对码）功率谱（局部）');
xlabel('f/Hz');
ylabel('G_a(f)');
ax = gca;
chart = ax.Children(1);
n = find(f==24000);
datatip(chart,f(n),Ga(n));
grid

image

此处实现绝对码的传号差分码编码，将输入的绝对码序列 [1,1,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,0,1,1,0,1,1,1] 通过编码后得到相对码序列 [1,0,0,1,1,1,0,1,1,0,0,0,0,0,0,1,1,1,0,1,1,0,1,0]，并转化为图(a) 中相应时域信号输出。

同时，通过计算功率谱函数，输出功率谱波形图。观察图(b,c) 中的功率谱可以发现，和绝对码基带信号类似的是，其主要为直流分量，频率较低，功率谱主要集中在低频部分，且带宽为B=fB=2.4×104B=f_B =2.4\times 10^4 Hz。

相移键控

将绝对码转化为相对码后，根据相对码对输入载波进行绝对调相，若为低电平 则相移为 0，高电平相移为π\pi 。输出后的b(t)b(t)即为相移键控后所得到的调制信号。

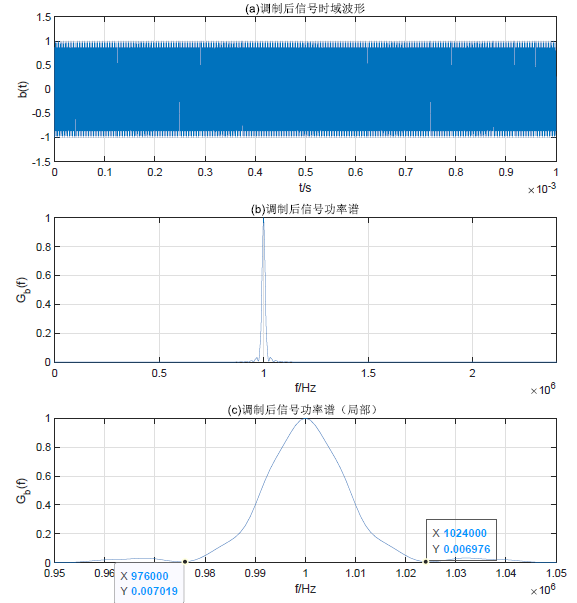
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
for i = 1 : L
    if Signal_relative(i) == 1
        bt((i-1)*Ns + 1 : i*Ns) = cos (2 * pi * fc * t((i-1)*Ns + 1 : i*Ns) + pi);
    else
        bt((i-1)*Ns + 1 : i*Ns) = cos (2 * pi * fc * t((i-1)*Ns + 1 : i*Ns));
    end
end

Gb =cpsd(bt,bt,[],[],Nfft,[],"twosided");

figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot (t, bt);
axis([0, TB * L, -1.5, 1.5 ]);
title ('(a)调制后信号时域波形');
xlabel('t/s');
ylabel('b(t)');
grid
subplot(3,1,2);
plot(f,abs(Gb)/max(abs(Gb)));
set(gca,'xlim',[0,2.4e6]);
title('(b)调制后信号功率谱');
xlabel('f/Hz');
ylabel('G_b(f)');
grid
subplot(3,1,3);
plot(f,abs(Gb)/max(abs(Gb)));
set(gca,'xlim',[0.95e6,1.05e6]);
title('(c)调制后信号功率谱（局部）');
xlabel('f/Hz');
ylabel('G_b(f)');
ax = gca;
chart = ax.Children(1);
n1 = find(f==1024000);
datatip(chart,f(n1),Gb(n1));
n2 = find(f==976000);
datatip(chart,f(n2),Gb(n2));
grid

image

若放大观察已调信号的时域波形图\(a) 可以看到，波形的相位变化点的分布符合相对码序列的分布规律。 从图(b)中可以看出调制信号的功率谱密度主要集中在 载波频率1 MHz 点处，带宽为B=2fB=4.8×104B=2f_B =4.8\times 10^4 Hz，与2DPSK码的功率谱特点一致。

高斯信道

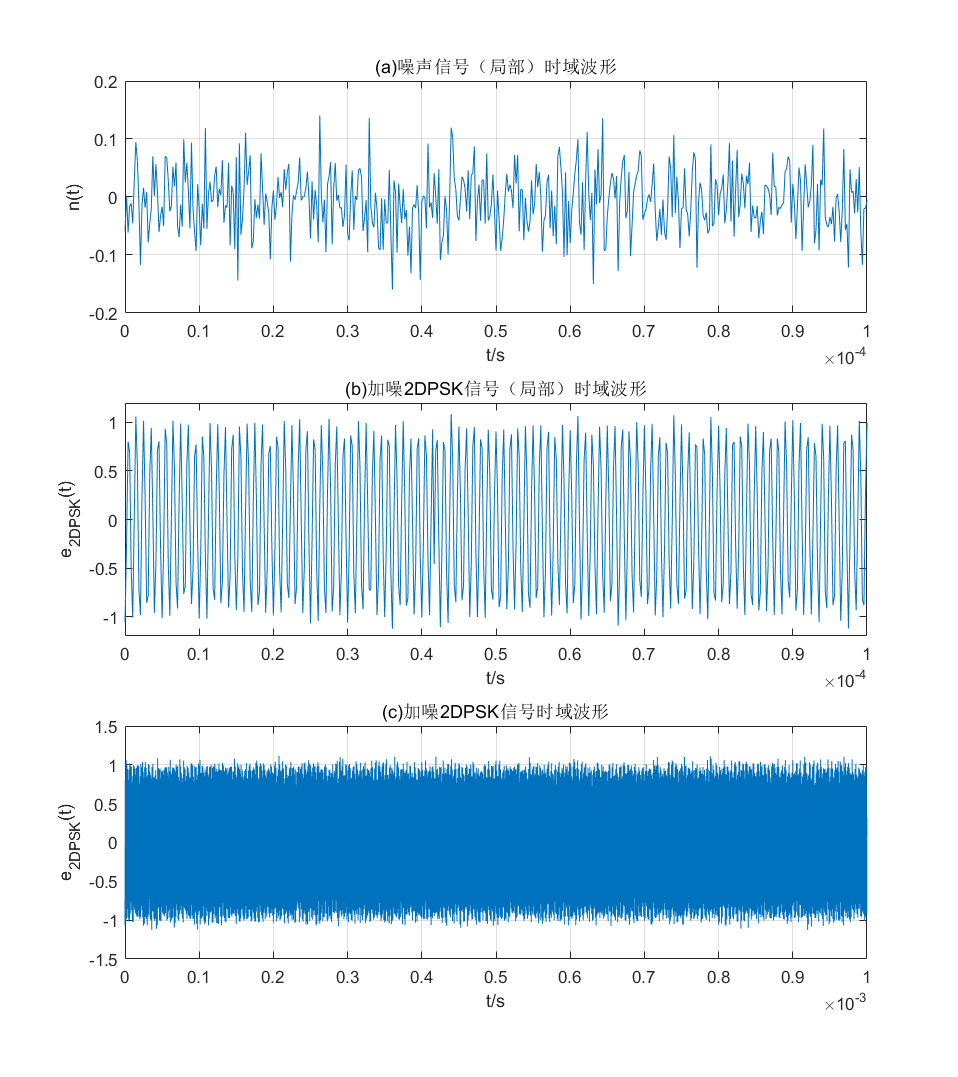
因题目要求信道采用高斯信道，这里生成μ=0, σ2=0.052\mu =0,~\sigma^2 =0.05^2的高斯噪声与调制后的信号相叠加，相移键控调制后的信号通过高斯信道后的频谱分布。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vn = 0.05;
nt = vn .* (randn(size(t))); %产生噪音
dpsk = (bt + nt);

figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot(t,nt);
grid
title('(a)噪声信号（局部）时域波形');
xlabel('t/s');
ylabel('n(t)');
axis([0 1e-4 -0.2 0.2]);
subplot(3,1,2);
plot(t,dpsk);
axis([0 1e-4 -1.2 1.2]);
title('(b)加噪2DPSK信号（局部）时域波形');
xlabel('t/s');
ylabel('e_{2DPSK}(t)');
subplot(3,1,3);
plot(t,dpsk);
title('(c)加噪2DPSK信号时域波形');
xlabel('t/s');
ylabel('e_{2DPSK}(t)');
grid

image

所产生的高斯信号与加噪后的噪声如图所示。

2DPSK解调

带通滤波器

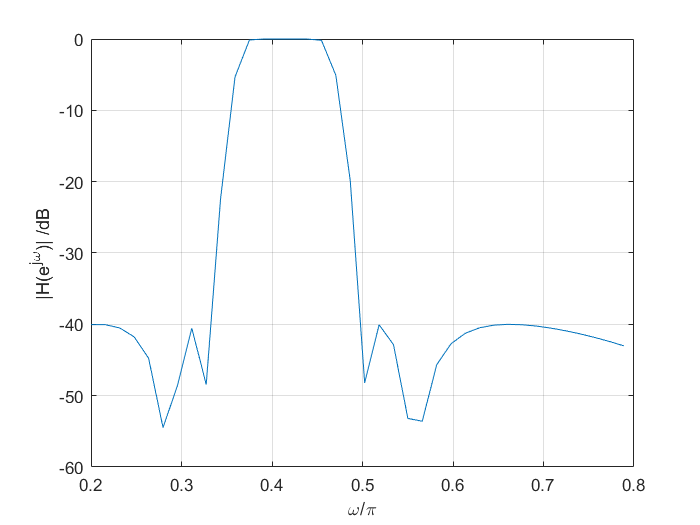
解调过程中，首先应该考虑高斯信道产生的噪声影响，故设计带通滤波器滤除 加噪2DPSK信号中的噪声，采用切比雪夫II型数字滤波器实现带通滤波器。这里设置采样频率为4.8 MHz，载波频率为1 MHz，故选取通带截止频率为fpl=0.9f_{pl} =0.9 MHz, fpu=1.1f_{pu} =1.1 MHz，且要求幅度失真大于1 dB，即通带最大衰减αp=1\alpha_p =1 dB。同时我们滤除小于fsl=0.8f_{sl} =0.8 MHz和大于fsu=1.2f_{su} =1.2 MHz的干扰和噪声，衰减大于 40 dB，即阻带最小衰减αs=40\alpha_s =40 dB。

1
2
3
4
5
6
7
8
9
10
11
12
13
Wpl = 2 *  9e5/fs; Wpu = 2  * 11e5/fs; Wsl = 2 * 8e5/fs; Wsu= 2  *12e5/fs; Rp = 1; Ra = 40;  % 滤波器指标
Wp = [Wpl, Wpu];
Ws = [Wsl, Wsu];
[N, Wso] = cheb2ord(Wp, Ws, Rp, Ra);     % 计算切比雪夫Ⅱ型数字滤波器的阶N和阻带边界频率Wso
[Bz, Az] = cheby2(N, Ra, Wso);           % 用双线性变换法设计切比雪夫Ⅱ型数字带通滤波器
ct = filter(Bz,Az,dpsk);

w = 0.2 * pi: 0.05 :  0.8 * pi;
[H, ~] = freqz(Bz ,Az, w); 
H = 20 * log10(abs(H));
figure;
plot(w/pi,H),grid on
xlabel('\omega/\pi') ;ylabel('|H(e^{j\omega})| /dB');

image

画出切比雪夫II型数字滤波器的幅频响应如图所示，可以看出符合上述数字带通滤波器设计要求。

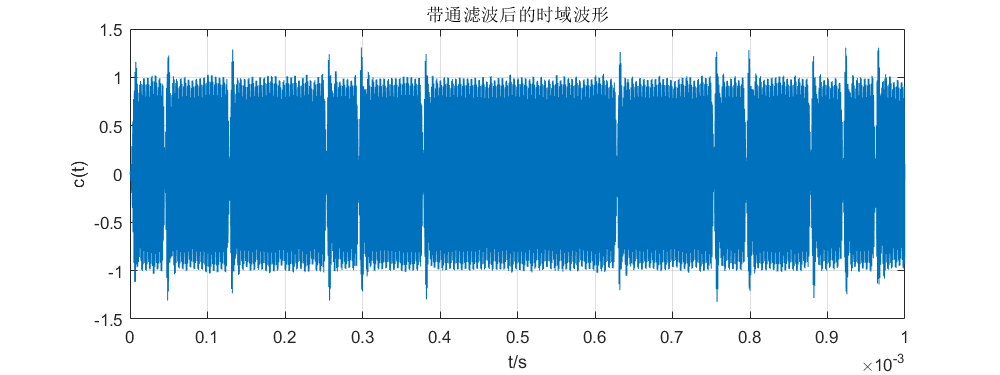
加噪2DPSK信号通过带通滤波器后得到滤除部分噪声和干扰的信号c(t)c(t)。

1
2
3
4
5
6
7
figure;
set(gcf,'position',[0,0,800,300],'color','w');
plot(t,ct);
title('带通滤波后的时域波形');
xlabel('t/s');
ylabel('c(t)');
grid

image

图所示信号与上图© 相比可发现谱线变得更加清晰，可清晰观察到倒相现象。

相乘器

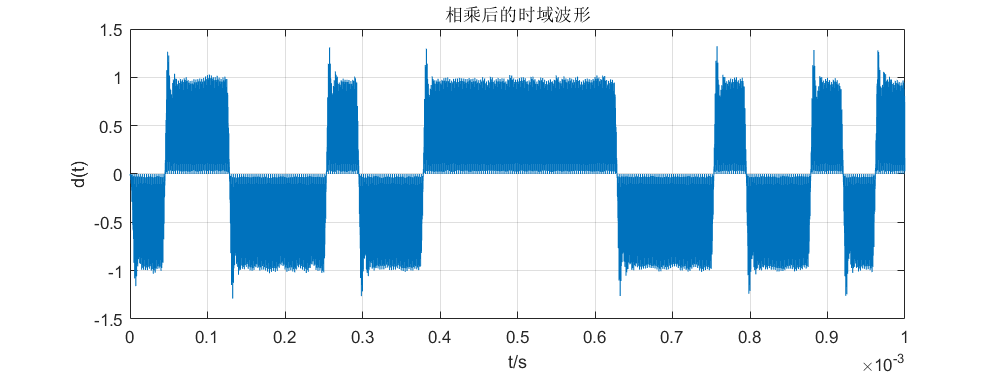
通过相乘器将带通滤波器输出的信号c(t)c(t)与本地载波cos⁡ωct\cos \omega_c t相乘，相乘器起 相位恢复的作用，相乘结果反映了前后码元的相位差。

1
2
3
4
5
6
7
8
9
10
dt = ct .* cos (2 * pi * fc * t);

figure;
set(gcf,'position',[0,0,800,300],'color','w');
plot(t, dt);
axis([0, TB * L, -1.5, 1.5]);
title('相乘后的时域波形');
xlabel('t/s');
ylabel('d(t)');
grid

image

观察图中的波形可以发现，相乘后的时域波形，横轴上方代表相对码中的 0，下方表示相对码中的 1，符合反向的相对 码序列[1,0,0,1,1,1,0,1,1,0,0,0,0,0,0,1,1,1,0, 1,1,0,1,0] 的分布规律。同时可以看到信号幅度减半，这是由于相乘器在应用积化和差时引入了一个12\frac{1}{2}的因子。

低通滤波器

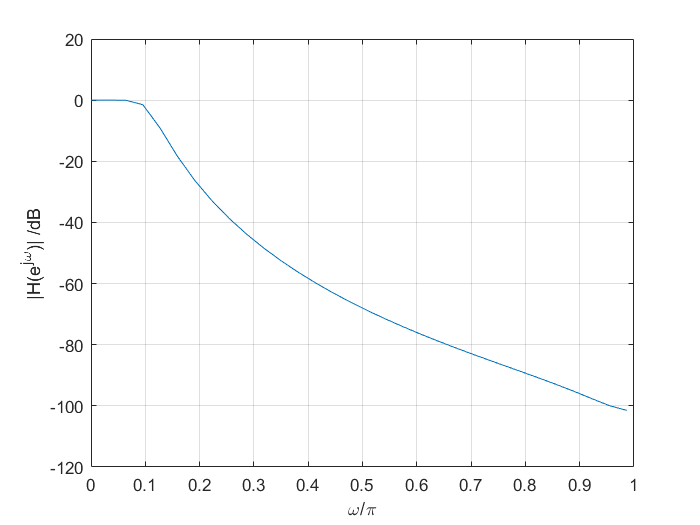
下面需要滤除载波1 MHz，设计低通滤波器滤除掉相乘器的输出信号 d(t) 的高频部分，便于后续抽样判决，所设计滤波器采用巴特沃斯模拟低通滤波器，并采用脉冲响应不变法将模拟滤波器转换为数字滤波器。这里我们将基带信号从已调波中滤出，从图 中可以看到基带信号集中在低频部分，故选取通带截止频率fp=0.2f_p =0.2 MHz，通带最大衰减αp=1\alpha_p =1 dB阻带截止频率fs=0.5f_s =0.5 MHz，阻带最小衰减αs=30\alpha_s =30 dB，采样频率为4.8 MHz。

1
2
3
4
5
6
7
8
9
10
11
12
[N,Wn] = buttord(2 * pi * 2e5, 2 * pi * 5e5, 1, 30,'s');
[Bs,As] = butter(N, Wn, 's');
[Bz,Az] = impinvar(Bs, As, fs); % 脉冲响应不变法，将模拟滤波器转换为数字滤波器
et = filter(Bz, Az, dt);


w = 0: 0.1 : pi;
[H, ~] = freqz(Bz ,Az, w); 
H = 20 * log10(abs(H));
figure;
plot(w/pi,H),grid on
xlabel('\omega/\pi') ;ylabel('|H(e^{j\omega})| /dB');

image

画出巴特沃斯低通滤波器的幅频响应如图所示，可以看出符合上述数字带通 滤波器设计要求。

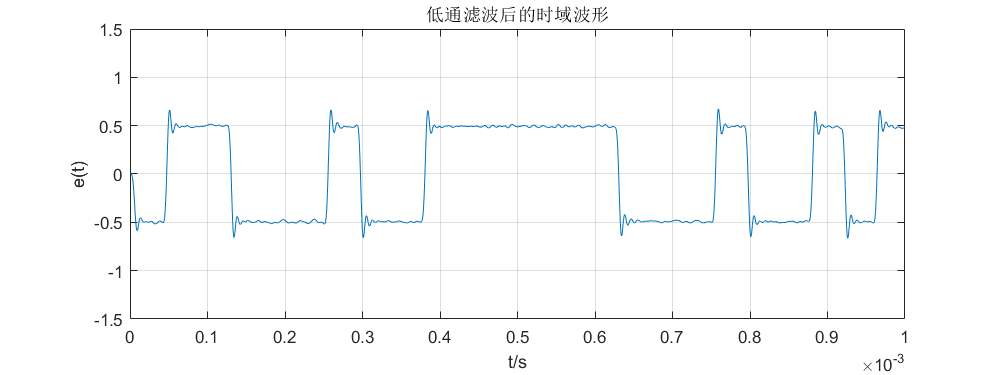
已调信号通过低通滤波器后得到滤除载波的信号e(t)e(t)。

1
2
3
4
5
6
7
8
figure;
set(gcf,'position',[0,0,800,300],'color','w');
plot (t, et);
axis([0, TB * L, -1.5, 1.5]);
title('低通滤波后的时域波形');
xlabel('t/s');
ylabel('e(t)');
grid

image

如图所示，时域波形是没有了载波恢复成了基带信号，下面需要进行抽样判决。可以看到曲线上出现了一些振铃噪声，这是因为sinc函数的拖尾被截断而导致，也印证了矩形信号无法完美实现。

抽样判决

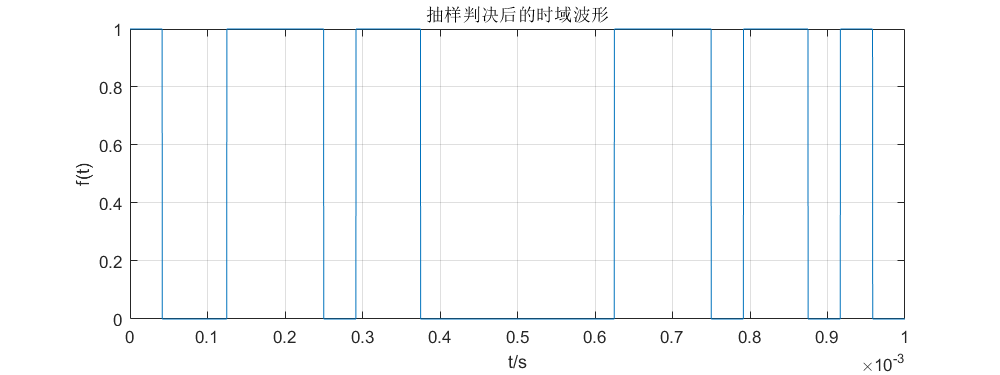
抽样判决器包括抽样、判决及码元形成，经抽样、判决后将码元再生，即可恢 复出数字序列。定时抽样脉冲（位同步信号）是很窄的脉冲，位于每个码元的 中央位置。通过将中央位置的码元幅度与门限电平（此处为 0 V）相比较，横轴 上方代表相对码中的 0，下方表示相对码中的 1，即可恢复相对码序列 [1,0,0,1,1,1,0,1,1,0,0,0,0,0,0,1,1,1,0, 1,1,0,1,0] 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
for i = 1 : L
    if et((2*i-1)*Ns/2) < 0
        ft((i-1)*Ns + 1 : i*Ns) = HL;
    else
        ft((i-1)*Ns + 1 : i*Ns) = LL;
    end
end

figure;
set(gcf,'position',[0,0,800,300],'color','w');
plot (t, ft);
title('抽样判决后的时域波形');
xlabel('t/s');
ylabel('f(t)');
grid

image

抽样判决后生成的数字序列如图所示，可以看到和 4(a) 的波形是完全一致。这相当于完成了2PSK的任务，但是2DPSK和2PSK还相差了码反变换。

码反变换

通过模二加运算实现码反变化，将当前相对码序列幅度与前一周期时刻幅度进 行模二加运算，即可恢复出绝对码波形。

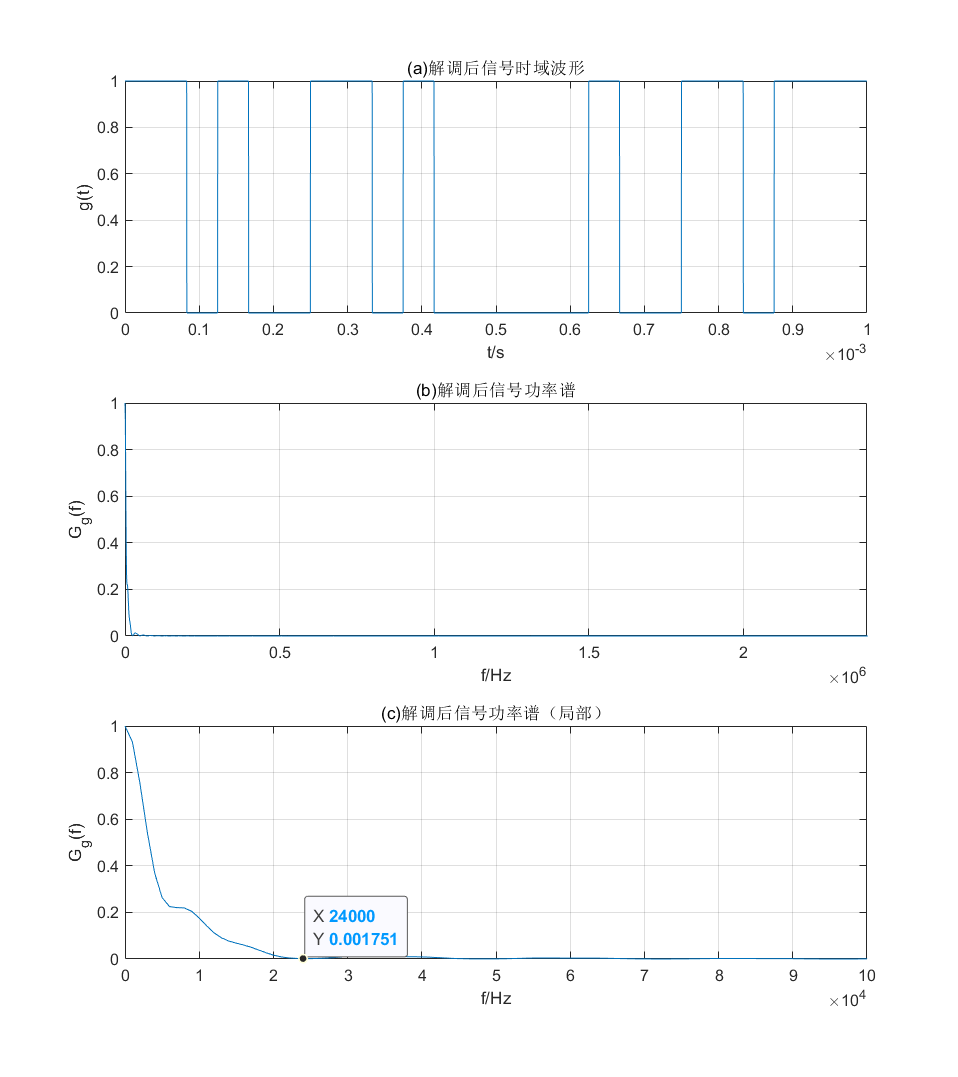
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
for i = 1 : L
    if (i==1)
        if (mod(ft(1), 2) == 1)
            gt(1:Ns) = HL;
        else
            gt(1:Ns) = LL;
        end
    elseif mod(ft((i-1)*Ns - 1)+ft((i-1)*Ns + 1),2)
        gt((i-1)*Ns + 1 : i*Ns) = HL;
    else
        gt((i-1)*Ns + 1 : i*Ns) = LL;
    end
end

Gg=cpsd(gt,gt,[],[],Nfft,fs,'twosided');

figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot (t, gt);
title ('(a)解调后信号时域波形');
xlabel('t/s');
ylabel('g(t)');
grid
subplot(3,1,2);
plot(f,abs(Gg)/max(abs(Gg)));
set(gca,'xlim',[0,2.4e6]);
title('(b)解调后信号功率谱');
xlabel('f/Hz');
ylabel('G_g(f)');
grid
subplot(3,1,3);
plot(f,abs(Gg)/max(abs(Gg)));
set(gca,'xlim',[0,0.1e6]);
title('(c)解调后信号功率谱（局部）');
xlabel('f/Hz');
ylabel('G_g(f)');
ax = gca;
chart = ax.Children(1);
n = find(f==24000);
datatip(chart,f(n),Gg(n));
grid

image

所得到的绝对码时间波形如图所示， 符合绝对码输入序列 [1,1,0,1,0,0,1,1,0,1,0,0,0,0,0,1,0,0,1,1,0,1,1,1] 的分布规律。解调后的信号功率谱中主要 为直流分量，低频信号，因此功率谱主要集中在低频部分。同时，带宽为B=fB=1TB=2.4×104B=f_B =\frac{1}{T_B }=2.4\times 10^4 Hz，恢复到单极性非归零码的性质。

五、输入输出波形的比较

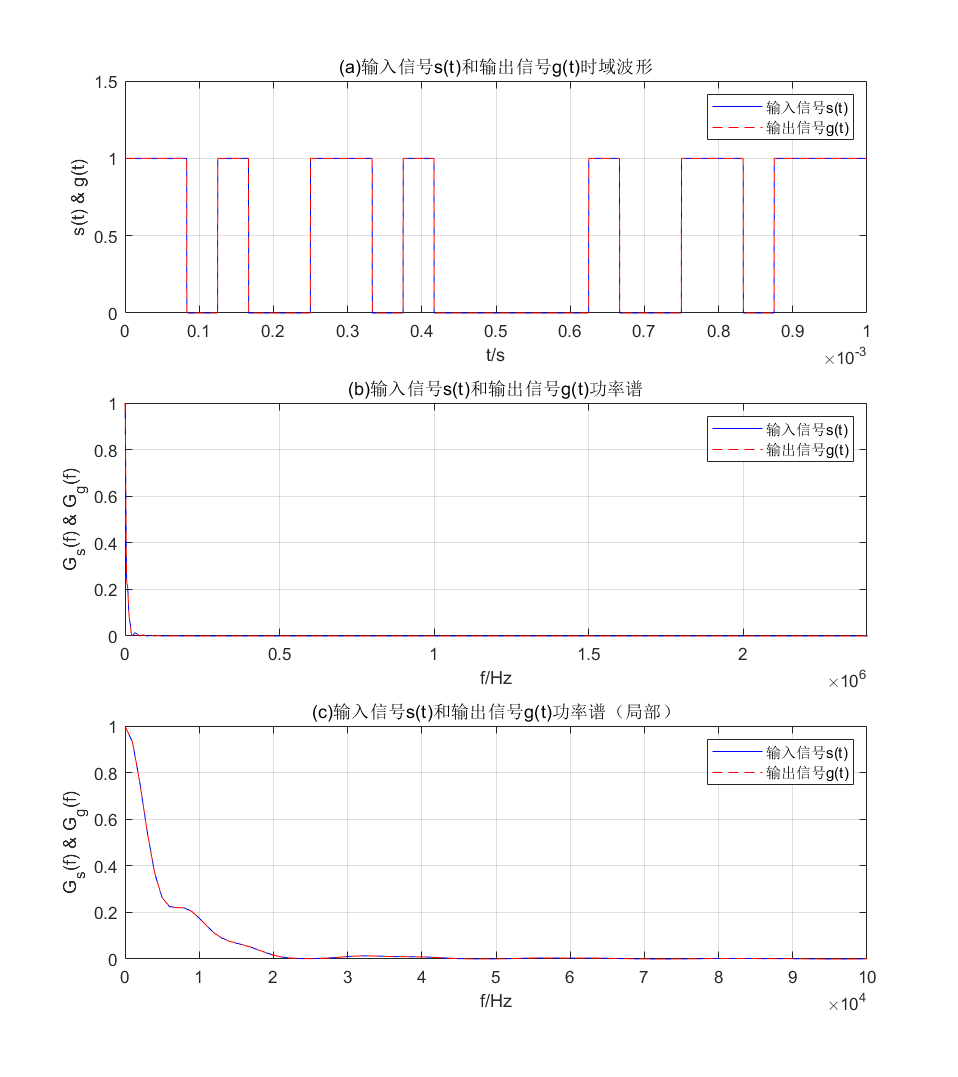
输入输出信号的时域波形和频域波形如图所示。从图可以看出时域波形和频域波形完全重合，说明数字 2DPSK 频带传输系统的设计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
figure;
set(gcf,'position',[0,0,800,900],'color','w');
subplot(3,1,1);
plot (t, st,"b", t, gt, "r--");
set(gca,'ylim',[0,1.5]);
legend('输入信号s(t)','输出信号g(t)');
title ('(a)输入信号s(t)和输出信号g(t)时域波形');
xlabel('t/s');
ylabel('s(t) & g(t)');
grid
subplot(3,1,2);
plot(f,abs(Gs)/max(abs(Gs)),"b",f,abs(Gg)/max(abs(Gg)),"r--");
legend('输入信号s(t)','输出信号g(t)');
set(gca,'xlim',[0,2.4e6]);
title('(b)输入信号s(t)和输出信号g(t)功率谱');
xlabel('f/Hz');
ylabel('G_s(f) & G_g(f)');
grid
subplot(3,1,3);
plot(f,abs(Gs)/max(abs(Gs)),"b",f,abs(Gg)/max(abs(Gg)),"r--");
legend('输入信号s(t)','输出信号g(t)');
set(gca,'xlim',[0,0.1e6]);
title('(c)输入信号s(t)和输出信号g(t)功率谱（局部）');
xlabel('f/Hz');
ylabel('G_s(f) & G_g(f)');
grid

image

六、心得体会

这次仿真实验我们实现了一个基本的通信系统模型，主要研究的是数字频带传输系统的设计与工作原理分析。

电院电子信息工程专业本学期开设的《通信原理》课程尚未进行到数字调制部分，在前期准备阶段，我们自学了相关章节，并构建了从数字调制部分到数字解调部分的原理框图。在数字调制部分，通过差分编码，将原始基带信号序列（绝对码形式）转变为相对码形式，克服了2PSK相位模糊性的缺点；以转换后的信号作为控制电平，控制本振信号的相移，从而生成二进制差分相移键控信号，信息挂载于载波上。信号在信道中传输时会受到干扰，我们添加了加性高斯噪声来模拟高斯信道。信道到达接收端，在进行数字解调前，需要让信号通过带通滤波器，以削弱高斯信道的噪声影响。解调采用的方式是相干解调，需要用与载波频率一致的本振信号参与解调。经滤波后的信号与本振信号相乘，再经过低通滤波器（低通滤波器的作用等同于包络检波），得到相对码形式的数字基带信号。经过抽样判决器，并经过码反变换，最终得到与原始信号相同的信息序列。

整个过程中我们遇到了很多问题，通过数学分析与反复试验得以解决。在信号码速一定的情况下，我们尝试了多组采样率与载波信号频率，观察信号时域图，选取最佳的组合；在相移键控部分，我们没有正确理解相对码与相移键控信号的关系，在向量构造上多次出现不匹配的情况，经推导解决；此外，我们还研究了数字角频率与模拟频率的数学关系，正确对各信号频谱的横坐标进行了标注。任务圆满完成。

本次实验综合运用了《通信原理》与算法相关知识，将理论与实践相结合，强化了我们系统分析与算法设计的能力。我们初步学习了现代通信系统的构成与运作方式，对数字编解码进行了实践，可谓受益匪浅。

参考文献

  1. 樊昌信，曹丽娜. 通信原理(第7版)[M]. 北京：国防工业出版社, 2012: 184-189.
  2. 史林，赵树杰. 数字信号处理[M]. 北京：科学出版社, 2007: 240, 258-259.

本文标题:【B测】数字2DPSK频带传输系统的设计

文章作者:Levitate_

发布时间:2021年04月22日 - 15:49:36

原始链接:https://levitate-qian.github.io/2021/04/22/b-test/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。