Wireless Communications (Andrea Goldsmith)学习笔记。
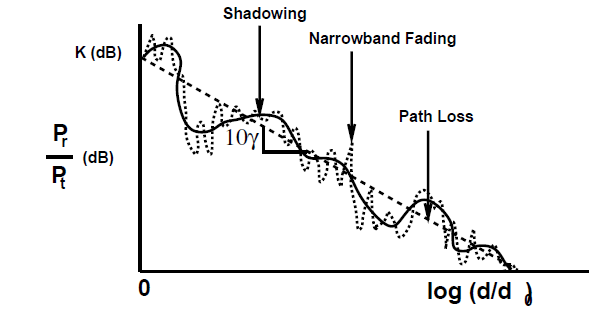
在第二章中,着重讨论的确知信道,但是实际中确知信道是极为少见的。第三章将通过随机时变冲激响应 (random time-varying impulse response)来刻画多径信道。路径损耗、阴影和多径模型共同刻画了信号传输过程中发射信号到接收信号之间的损耗。
多径信道的两个基本特征:
时延扩展(delay spread) :这个延迟扩散等于第一个收到的信号分量(LOS或多径)到达与单个传输脉冲相关的最后一个收到的信号分量之间的时间延迟。时变性(time-varying) :如果我们从一个移动 的发射器重复发射脉冲,我们将观察到每个脉冲对应的**振幅(amplitudes)、延迟(delays)和多径分量(number of multipath components)**的变化。
散射函数其实有点《雷达原理与系统》中雷达波形模糊函数的意味在里面了。
χ ( τ , f d ) = ∫ − ∞ ∞ u ( t ) u ∗ ( t + τ ) e j 2 π f d t d t \chi\left(\tau, f_{d}\right)=\int_{-\infty}^{\infty} u(t) u^{*}(t+\tau) e^{j 2 \pi f_{d} t} \mathrm{~d} t
χ ( τ , f d ) = ∫ − ∞ ∞ u ( t ) u ∗ ( t + τ ) e j 2 π f d t d t
本章的主要思路是:先给出一个时变信道的冲激响应(Time-Varying Channel Impulse Response),利用随机信号分析的知识应用到窄带衰落模型(the channel bandwidth is small compared to the inverse delay spread.B < 1 Δ τ B<\frac 1{\Delta\tau} B < Δ τ 1
发射信号:
s ( t ) = ℜ [ u ( t ) e j 2 π f c t ] s(t)=\Re[u(t)e^{j2\pi f_ct}]
s ( t ) = ℜ [ u ( t ) e j 2 π f c t ]
发射基带信号u ( t ) u(t) u ( t ) B u B_u B u
接收信号:
e q 2 r ( t ) = ℜ { ∑ n = 0 N ( t ) α n ( t ) u ( t − τ n ( t ) ) e j ( 2 π f c ( t − τ n ( t ) ) + ϕ D n ( t ) ) } {eq2}
r(t)=\Re\left\{\sum_{n=0}^{N(t)} \alpha_{n}(t) u\left(t-\tau_{n}(t)\right) e^{j\left(2 \pi f_{c}\left(t-\tau_{n}(t)\right)+\phi_{D_{n}(t)}\right)}\right\}
e q 2 r ( t ) = ℜ ⎩ ⎨ ⎧ n = 0 ∑ N ( t ) α n ( t ) u ( t − τ n ( t ) ) e j ( 2 π f c ( t − τ n ( t ) ) + ϕ D n ( t ) ) ⎭ ⎬ ⎫
其中,N ( t ) N(t) N ( t ) α n ( t ) \alpha_n(t) α n ( t ) n n n τ n ( t ) = r n ( t ) c \tau_n(t)=\frac{r_n(t)}{c} τ n ( t ) = c r n ( t ) n n n r n ( t ) r_n(t) r n ( t ) ϕ D n ( t ) \phi_{D_n}(t) ϕ D n ( t ) n n n 时变 的。
对于单一反射体,接收信号的参数:
幅度 变化:α n ( t ) \alpha_n(t) α n ( t ) n n n 频率 变化主要有两方面组成:时延τ n ( t ) \tau_n(t) τ n ( t ) e − j 2 π f C τ n ( t ) e^{-j2\pi f_C \tau_n(t)} e − j 2 π f C τ n ( t ) ϕ D n ( t ) = ∫ t 2 π v cos θ n ( t ) λ d τ \phi_{D_n}(t)=\int_t 2\pi \frac{v\cos\theta_n(t)}{\lambda}\ d\tau ϕ D n ( t ) = ∫ t 2 π λ v cos θ n ( t ) d τ
值得注意的是,在雷达中的多普勒频移刚好和这里差了一个2倍的关系,这是因为对于收发公用天线的雷达,需要考虑去程和回程。在雷达回波信号模型中,回波信号的基带复包络为
S ( t ) = A s e ( t − τ 0 ) exp ( j 2 π f d t ) S(t)=As_e(t-\tau_0)\exp (j2\pi f_dt)
S ( t ) = A s e ( t − τ 0 ) exp ( j 2 π f d t )
多普勒频移项为j 2 π f d t = j 2 π 2 v cos θ f 0 c t = j 2 π 2 v cos θ λ t j2\pi f_d t=j 2\pi \frac{2v\cos\theta f_0}{c}t=j 2\pi \frac{2v\cos\theta }{\lambda}t j 2 π f d t = j 2 π c 2 v cos θ f 0 t = j 2 π λ 2 v cos θ t
可分辨性(resolvable) :对于时延分别为τ 1 , τ 2 \tau_1,\tau_2 τ 1 , τ 2
∣ τ 1 − τ 2 ∣ ≫ 1 B u |\tau_1-\tau_2|\gg \frac{1}{B_u}
∣ τ 1 − τ 2 ∣ ≫ B u 1
则称这两个径是可分辨的。
这里的1 B u \frac{1}{B_u} B u 1 Δ τ \Delta\tau Δ τ
Δ τ = ∫ − ∞ ∞ ∣ χ ( τ , 0 ) ∣ 2 d τ ∣ χ ( 0 , 0 ) ∣ 2 = 2 π ∫ − ∞ ∞ ∣ U ( ω ) ∣ 4 d ω [ ∫ − ∞ ∞ ∣ U ( ω ) ∣ 2 d ω ] 2 = 1 B \Delta \tau=\frac{\int_{-\infty}^{\infty}|\chi(\tau, 0)|^{2} \mathrm{~d} \tau}{|\chi(0,0)|^{2}}=2 \pi \frac{\int_{-\infty}^{\infty}|U(\omega)|^{4} \mathrm{~d} \omega}{\left[\int_{-\infty}^{\infty}|U(\omega)|^{2} \mathrm{~d} \omega\right]^{2}}=\frac{1}{B}
Δ τ = ∣ χ ( 0 , 0 ) ∣ 2 ∫ − ∞ ∞ ∣ χ ( τ , 0 ) ∣ 2 d τ = 2 π [ ∫ − ∞ ∞ ∣ U ( ω ) ∣ 2 d ω ] 2 ∫ − ∞ ∞ ∣ U ( ω ) ∣ 4 d ω = B 1
其中,χ ( τ , f d ) \chi(\tau,f_d) χ ( τ , f d ) B B B
Δ R = c Δ τ 2 = c 2 B \Delta R=\frac{c\Delta\tau}{2}=\frac{c}{2B}
Δ R = 2 c Δ τ = 2 B c
而可分辨性的定义即表明当两径时延差远大于时延分辨率时,两径是可分辨的,对应于雷达中的概念就是当两个目标对应回波延时差大于某一距离分辨率,两个目标在距离上是可以分辨的。这也正反映出窄带信道和宽带信道的区别。窄带信道,我们将所有多径分量都看作时一个独立反射体反射出的,对应距离上无法分辨;宽带信道,我们可以将多径分量看作是不同反射体反射出的,对应距离上可以分辨。
参数α n ( t ) , τ n ( t ) , ϕ D n ( t ) \alpha_n(t),\tau_n(t),\phi_{D_n}(t) α n ( t ) , τ n ( t ) , ϕ D n ( t )
一由ϕ n ( t ) = 2 π f c τ n ( t ) − ϕ D n ( t ) \phi_{n}(t)=2\pi f_c\tau_n(t)-\phi_{D_n}(t) ϕ n ( t ) = 2 π f c τ n ( t ) − ϕ D n ( t )
r ( t ) = ℜ { [ ∑ n = 0 N ( t ) α n ( t ) e − j ϕ n ( t ) u ( t − τ n ( t ) ) ] e j 2 π f c t } r(t)=\Re\left\{\left[\sum_{n=0}^{N(t)} \alpha_{n}(t) e^{-j \phi_{n}(t)} u\left(t-\tau_{n}(t)\right)\right] e^{j 2 \pi f_{c} t}\right\}
r ( t ) = ℜ ⎩ ⎨ ⎧ ⎣ ⎡ n = 0 ∑ N ( t ) α n ( t ) e − j ϕ n ( t ) u ( t − τ n ( t ) ) ⎦ ⎤ e j 2 π f c t ⎭ ⎬ ⎫
二由时变系统分析(基带输入信号通过时变信道再上变频到载频)可知
r ( t ) = ℜ { ( ∫ − ∞ ∞ c ( τ , t ) u ( t − τ ) d τ ) e j 2 π f c t } r(t)=\Re\left\{\left(\int_{-\infty}^{\infty} c(\tau, t) u(t-\tau) d \tau\right) e^{j 2 \pi f_{c} t}\right\}
r ( t ) = ℜ { ( ∫ − ∞ ∞ c ( τ , t ) u ( t − τ ) d τ ) e j 2 π f c t }
其中,c ( τ , t ) c(\tau,t) c ( τ , t ) ( t − τ ) (t-\tau) ( t − τ ) t t t
则可获得(离散)等效基带信道的时变脉冲响应, ϕ n = e − j 2 π f C τ n ( t ) \phi_n=e^{-j2\pi f_C \tau_n(t)} ϕ n = e − j 2 π f C τ n ( t )
c ( τ , t ) = ∑ n = 0 N ( t ) α n ( t ) e − j ϕ n ( t ) δ ( τ − τ n ( t ) ) c(\tau, t)=\sum_{n=0}^{N(t)} \alpha_{n}(t) e^{-j \phi_{n}(t)} \delta\left(\tau-\tau_{n}(t)\right)
c ( τ , t ) = n = 0 ∑ N ( t ) α n ( t ) e − j ϕ n ( t ) δ ( τ − τ n ( t ) )
将求和变成积分,即可得到(连续)时变脉冲响应
c ( τ , t ) = ∫ α ( ξ , t ) e − j ϕ ( ξ , t ) δ ( τ − ξ ) d ξ = α ( τ , t ) e − j ϕ ( τ , t ) c(\tau, t)=\int \alpha(\xi, t) e^{-j \phi(\xi, t)} \delta(\tau-\xi) d \xi=\alpha(\tau, t) e^{-j \phi(\tau, t)}
c ( τ , t ) = ∫ α ( ξ , t ) e − j ϕ ( ξ , t ) δ ( τ − ξ ) d ξ = α ( τ , t ) e − j ϕ ( τ , t )
时不变信道的脉冲响应就是将上述两式的t t t
衰落(fading) :Rapid phase changes in each multipath component gives rise to constructive and destructive addition of the multipath components comprising the received signal, which in turn causes rapid variation in the received signal strength. (每个多径分量的快速相位变化引起构成接收信号的多径分量的叠加,这反过来又引起接收信号强度的快速变化。这种现象,称为衰落 。)
time delay(时延扩展)T m ≪ 1 B T_m\ll\frac 1B T m ≪ B 1
time delay(时延扩展)大,多径分量可分辨,则为宽带衰落信道。宽带衰落中的可分辨分量实际上就是若干不可分辨分量的叠加。
在时变信道中,多径时延随时间变化,所以time delay T m T_m T m
窄带衰落模型(Narrowband fading model)中,时延扩展T m T_m T m 1 B \frac 1B B 1
对于窄带衰落模型,所有分量的时延不可分辨,τ i = τ \tau_i=\tau τ i = τ
r ( t ) = ℜ { u ( t ) e j 2 π f c t ( ∑ n α n ( t ) e − j ϕ n ( t ) ) } r(t)=\Re\left\{u(t) e^{j 2 \pi f_{c} t}\left(\sum_{n} \alpha_{n}(t) e^{-j \phi_{n}(t)}\right)\right\}
r ( t ) = ℜ { u ( t ) e j 2 π f c t ( n ∑ α n ( t ) e − j ϕ n ( t ) ) }
令u ( t ) = 1 u(t)=1 u ( t ) = 1 s ( t ) = ℜ { e j 2 π f c t e j ϕ 0 ( t ) } s(t)=\Re\left\{ e^{j 2 \pi f_{c} t}e^{j\phi_0(t)}\right\} s ( t ) = ℜ { e j 2 π f c t e j ϕ 0 ( t ) }
r ( t ) = ℜ { e j 2 π f c t ( ∑ n α n ( t ) e − j ϕ n ( t ) ) } = r I ( t ) cos 2 π f c t − r Q ( t ) sin 2 π f c t r(t)=\Re\left\{ e^{j 2 \pi f_{c} t}\left(\sum_{n} \alpha_{n}(t) e^{-j \phi_{n}(t)}\right)\right\}=r_I(t)\cos 2\pi f_c t-r_Q(t)\sin 2\pi f_c t
r ( t ) = ℜ { e j 2 π f c t ( n ∑ α n ( t ) e − j ϕ n ( t ) ) } = r I ( t ) cos 2 π f c t − r Q ( t ) sin 2 π f c t
即对其进行模拟正交检波得到
同相分量(in-phase):r I ( t ) = ∑ n = 1 N ( t ) α n ( t ) cos ϕ n ( t ) r_I(t)=\sum_{n=1}^{N(t)}\alpha_n(t)\cos\phi_n(t) r I ( t ) = ∑ n = 1 N ( t ) α n ( t ) cos ϕ n ( t )
正交分量(quadrature):r Q ( t ) = ∑ n = 1 N ( t ) α n ( t ) sin ϕ n ( t ) r_Q(t)=\sum_{n=1}^{N(t)}\alpha_n(t)\sin\phi_n(t) r Q ( t ) = ∑ n = 1 N ( t ) α n ( t ) sin ϕ n ( t )
相移:ϕ n ( t ) = 2 π f c τ n ( t ) − ϕ D n − ϕ 0 \phi_n(t)=2\pi f_c\tau_n(t)-\phi_{D_n}-\phi_0 ϕ n ( t ) = 2 π f c τ n ( t ) − ϕ D n − ϕ 0
在不考虑LOS分量的前提下考虑同相分量和正交分量。同时我们认为幅度、多径的时延和多普勒频移都是缓变的。
由《随机信号分析》有,N ( t ) N(t) N ( t ) r I ( t ) , r Q ( t ) r_I(t),r_Q(t) r I ( t ) , r Q ( t ) α n ( t ) \alpha_n(t) α n ( t ) ϕ n ( t ) \phi_n(t) ϕ n ( t )
均值:2 π f c τ n 2\pi f_c\tau_n 2 π f c τ n
自相关(Autocorrelation)、互相关(Cross Correlation)
接收信号的同相分量和正交分量时正交且不相关的。
自相关函数:(为了方便理解,这里的书写方式与《随机信号分析》保持一致)同相分量的自相关函数为
A r I ( t , t + τ ) = 1 2 ∑ n E [ α n 2 ] E [ cos 2 π v τ cos θ n λ ] = A r I ( τ ) A_{r_I}(t,t+\tau)=\frac 12\sum_nE[\alpha_n^2]E\left[\cos\frac{2\pi v\tau\cos\theta_n}{\lambda}\right]=A_{r_I}(\tau)
A r I ( t , t + τ ) = 2 1 n ∑ E [ α n 2 ] E [ cos λ 2 π v τ cos θ n ] = A r I ( τ )
由于自相关与t t t A r I ( t ) = A r Q ( t ) A_{r_I}(t)=A_{r_Q}(t) A r I ( t ) = A r Q ( t )
互相关函数:
A r I , r Q ( t , t + τ ) = 1 2 ∑ n E [ α n 2 ] E [ sin 2 π v τ cos θ n λ ] = A r I , r Q ( τ ) = − A r Q , r I ( τ ) A_{r_I,r_Q}(t,t+\tau)=\frac 12\sum_nE[\alpha_n^2]E\left[\sin\frac{2\pi v\tau\cos\theta_n}{\lambda}\right]=A_{r_I,r_Q}(\tau)=-A_{r_Q,r_I}(\tau)
A r I , r Q ( t , t + τ ) = 2 1 n ∑ E [ α n 2 ] E [ sin λ 2 π v τ cos θ n ] = A r I , r Q ( τ ) = − A r Q , r I ( τ )
同样互相关函数也是WSS。
接收信号的自相关函数:
A r ( τ ) = A r I ( τ ) cos ( 2 π f c τ ) + A r I , r Q ( τ ) sin ( 2 π f c τ ) A_{r}(\tau)=A_{r_{I}}(\tau) \cos \left(2 \pi f_{c} \tau\right)+A_{r_{I}, r_{Q}}(\tau) \sin \left(2 \pi f_{c} \tau\right)
A r ( τ ) = A r I ( τ ) cos ( 2 π f c τ ) + A r I , r Q ( τ ) sin ( 2 π f c τ )
对于均匀分布的相位,同相分量和正交分量服从零均值联合高斯分布。功率的分布就是包络平方的分布。
不考虑LOS分量包络的分布(窄带高斯噪声包络的分布)——瑞利分布(Rayleigh-distributed)
p Z ( z ) = 2 z P ˉ r exp [ − z 2 P ˉ r ] = z σ 2 exp [ − z 2 2 σ 2 ] , x ≥ 0 p_{Z}(z)=\frac{2 z}{\bar P_{r}} \exp \left[-\frac{z^{2}} {\bar P_{r}}\right]=\frac{z}{\sigma^{2}} \exp \left[-\frac{z^{2}}{2 \sigma^{2}}\right], \quad x \geq 0
p Z ( z ) = P ˉ r 2 z exp [ − P ˉ r z 2 ] = σ 2 z exp [ − 2 σ 2 z 2 ] , x ≥ 0
P ˉ r \bar P_r P ˉ r
不考虑LOS分量包络平方(功率)的分布(窄带高斯噪声包络的分布)——均值为2 σ 2 2\sigma^2 2 σ 2
P Z 2 ( x ) = 1 P r e − x P r = 1 2 σ 2 e − x 2 σ 2 , x ≥ 0 P_{Z^2}(x)=\frac{1}{P_r}e^{-\frac x{P_r}}=\frac{1}{2\sigma^2}e^{-\frac x{2\sigma^2}},x\ge 0
P Z 2 ( x ) = P r 1 e − P r x = 2 σ 2 1 e − 2 σ 2 x , x ≥ 0
考虑LOS分量包络的分布(窄带高斯噪声+信号包络的分布)——莱斯分布(广义瑞利分布,Rician distribution)
p Z ( z ) = z σ 2 exp [ − ( z 2 + s 2 ) 2 σ 2 ] I 0 ( z s σ 2 ) , z ≥ 0 p_{Z}(z)=\frac{z}{\sigma^{2}} \exp \left[\frac{-\left(z^{2}+s^{2}\right)}{2 \sigma^{2}}\right] I_{0}\left(\frac{z s}{\sigma^{2}}\right), \quad z \geq 0
p Z ( z ) = σ 2 z exp [ 2 σ 2 − ( z 2 + s 2 ) ] I 0 ( σ 2 z s ) , z ≥ 0
其中,s 2 = α 0 2 s^2=\alpha_0^2 s 2 = α 0 2 2 σ 2 2\sigma^2 2 σ 2 I 0 ( x ) I_0(x) I 0 ( x )
考虑LOS分量包络平方(功率)的分布(窄带高斯噪声+信号包络的分布)——自由度n = 2 n=2 n = 2
包络分布的经验公式——Nakagami fading distribution
p Z ( z ) = 2 m m z 2 m − 1 Γ ( m ) P ˉ r m exp [ − m z 2 P ˉ r ] , m ≥ 0.5 p_{Z}(z)=\frac{2 m^{m} z^{2 m-1}}{\Gamma(m)\bar P_{r}^{m}} \exp \left[\frac{-m z^{2}}{\bar P_{r}}\right], \quad m \geq 0.5
p Z ( z ) = Γ ( m ) P ˉ r m 2 m m z 2 m − 1 exp [ P ˉ r − m z 2 ] , m ≥ 0 . 5
P ˉ r \bar P_r P ˉ r m = 1 m=1 m = 1 m = ∞ m=\infty m = ∞ m = ( K + 1 ) 2 2 K + 1 m=\frac{(K+1)^2}{2K+1} m = 2 K + 1 ( K + 1 ) 2 K K K
包络平方(功率)分布的经验公式
p Z 2 ( x ) = ( m P r ) m x m − 1 Γ ( m ) exp ( − m x P r ) p_{Z^{2}}(x)=\left(\frac{m}{P_{r}}\right)^{m} \frac{x^{m-1}}{\Gamma(m)} \exp \left(\frac{-m x}{P_{r}}\right)
p Z 2 ( x ) = ( P r m ) m Γ ( m ) x m − 1 exp ( P r − m x )
Level Crossing Rate(电平通过率)L Z L_Z L Z Z Z Z
L Z = N Z T = ∫ − ∞ 0 z ˙ p ( Z , z ˙ ) d z ˙ L_Z=\frac{N_Z}{T}=\int_{-\infty}^{0}\dot zp(Z,\dot z)\ \mathrm{d}\dot z
L Z = T N Z = ∫ − ∞ 0 z ˙ p ( Z , z ˙ ) d z ˙
其中,Z Z Z z ˙ \dot z z ˙
莱斯衰落的Level Crossing Rate:
L Z = 2 π ( K + 1 ) f D ρ e − K − ( K + 1 ) ρ 2 I 0 ( 2 ρ K ( K + 1 ) ) L_{Z}=\sqrt{2 \pi(K+1)} f_{D} \rho e^{-K-(K+1) \rho^{2}} I_{0}(2 \rho \sqrt{K(K+1)})
L Z = 2 π ( K + 1 ) f D ρ e − K − ( K + 1 ) ρ 2 I 0 ( 2 ρ K ( K + 1 ) )
瑞利衰落的Level Crossing Rate:
L Z = 2 π f D ρ e − ρ 2 L_{Z}=\sqrt{2 \pi} f_{D} \rho e^{-\rho^{2}}
L Z = 2 π f D ρ e − ρ 2
其中,ρ = Z P ˉ r \rho=\frac{Z}{\bar P_r} ρ = P ˉ r Z
average signal fade duration(平均衰减时长)t ˉ z \bar t_z t ˉ z Z Z Z
t ˉ Z = 1 T L Z ∑ i = 1 L Z T t i ≈ p ( z ( t ) < Z ) L Z = 小于Z的总时间/单位时间 下穿过Z的次数/单位时间 \bar{t}_{Z}=\frac{1}{T L_{Z}} \sum_{i=1}^{L_{Z} T} t_{i} \approx \frac{p(z(t)<Z)}{L_{Z}}=\frac{\text{小于Z的总时间/单位时间}}{\text{下穿过Z的次数/单位时间}}
t ˉ Z = T L Z 1 i = 1 ∑ L Z T t i ≈ L Z p ( z ( t ) < Z ) = 下穿过 Z 的次数 / 单位时间 小于 Z 的总时间 / 单位时间
瑞利分布的average signal fade duration:
t ˉ Z = e ρ 2 − 1 ρ f D 2 π \bar{t}_{Z}=\frac{e^{\rho^{2}}-1}{\rho f_{D} \sqrt{2 \pi}}
t ˉ Z = ρ f D 2 π e ρ 2 − 1
average signal fade duration随多普勒频移的增加而减少。
The average fade duration indicates the number of bits or symbols affected by a deep fade.
有限状态马尔可夫信道(FSMC)是一个比较简单的模型,它捕捉到了平衰落信道的主要特征。在这个模型中,衰落被近似为一个离散时间马尔可夫过程,时间被离散为一个给定的间隔T T T T T T
宽带衰落模型(Wideband fading models)中,多出了多径时延扩展导致的失真(distortion due to the multipath delay)。若发射脉冲宽度为T T T T + T m T+T_m T + T m T m T_m T m
当T m ≪ T T_m\ll T T m ≪ T
当T m ≫ T T_m\gg T T m ≫ T
解决方法:equalization(均衡), multicarrier modulation(多载波调制), and spread spectrum(扩频)
对于宽带衰落模型,u ( t − τ n ( t ) ) ≈ u ( t ) u(t - \tau_n(t))\approx u(t) u ( t − τ n ( t ) ) ≈ u ( t ) τ n \tau_n τ n ϕ n ( t ) \phi_n(t) ϕ n ( t )
对于窄带信道,我们主要从幅度和相位随机过程来刻画。对于宽带信道,必须要考虑**多径时延扩展(multipath delay spread)和信道时变(time-variations associated with the channel)**的影响。
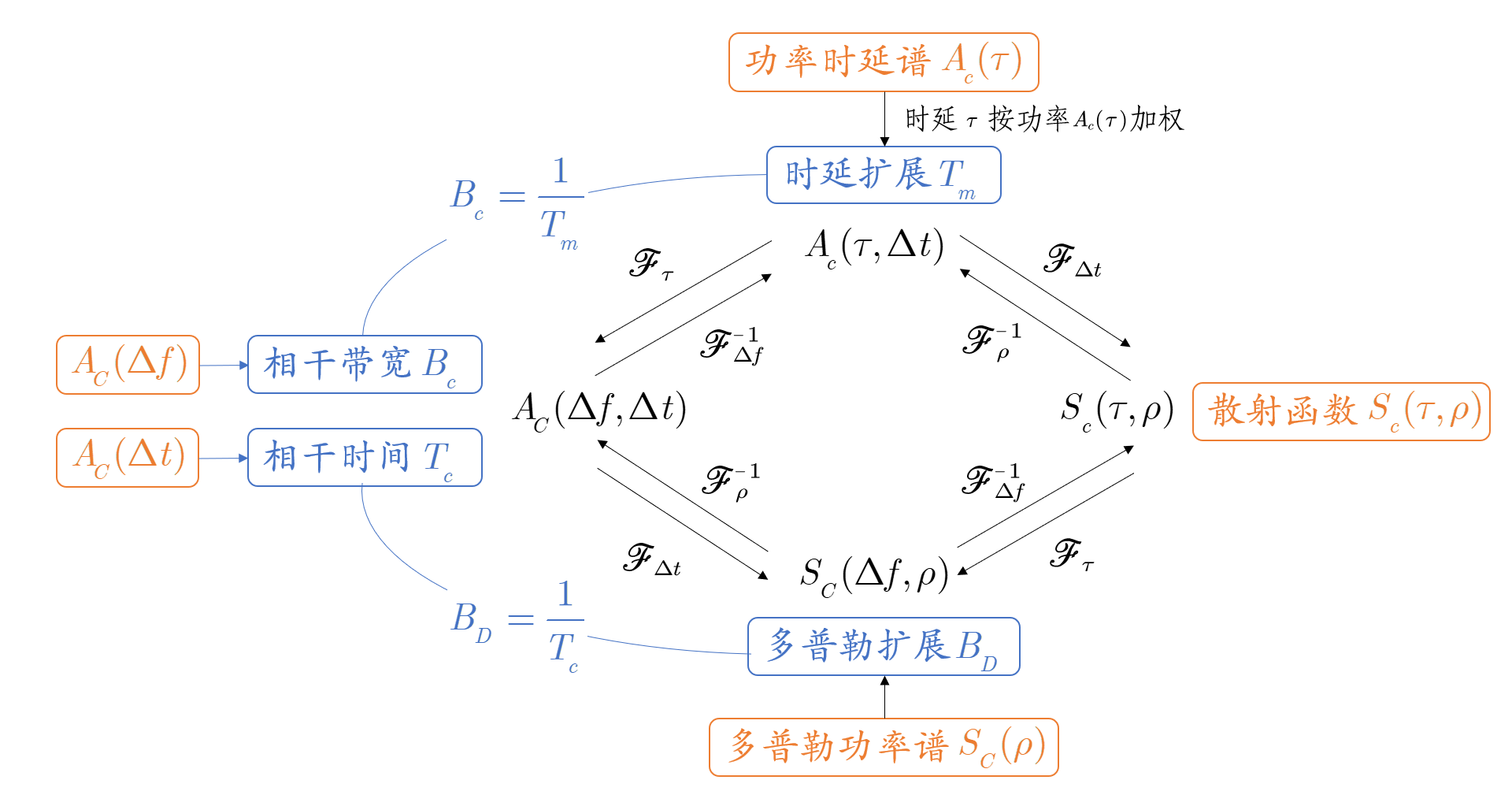
deterministic scattering function(确知散射函数):
c ( τ , t ) ⟷ S c ( τ , ρ ) = ∫ − ∞ ∞ c ( τ , t ) e − j 2 π ρ t d t c(\tau,t)\longleftrightarrow S_{c}(\tau, \rho)=\int_{-\infty}^{\infty} c(\tau, t) e^{-j 2 \pi \rho t}\ \mathrm{d} t
c ( τ , t ) ⟷ S c ( τ , ρ ) = ∫ − ∞ ∞ c ( τ , t ) e − j 2 π ρ t d t
S c ( τ , ρ ) S_{c}(\tau, \rho) S c ( τ , ρ ) c ( τ , t ) c(\tau,t) c ( τ , t ) t t t ρ \rho ρ
random scattering function(随机散射函数)
考虑到c ( τ , t ) c(\tau,t) c ( τ , t ) A c ( τ 1 , τ 2 ; t , t + Δ t ) A_c(\tau_1,\tau_2;t,t+\Delta t) A c ( τ 1 , τ 2 ; t , t + Δ t ) A c ( τ 1 , τ 2 ; Δ t ) A_c(\tau_1,\tau_2;\Delta t) A c ( τ 1 , τ 2 ; Δ t ) τ 1 ≠ τ 2 \tau_1\neq\tau_2 τ 1 = τ 2
E [ c ∗ ( τ 1 ; t ) c ( τ 2 ; t + Δ t ) ] = A c ( τ 1 ; Δ t ) δ [ τ 1 − τ 2 ] ≜ A c ( τ ; Δ t ) E\left[c^{*}\left(\tau_{1} ; t\right) c\left(\tau_{2} ; t+\Delta t\right)\right]=A_{c}\left(\tau_{1} ; \Delta t\right) \delta\left[\tau_{1}-\tau_{2}\right] \triangleq A_{c}(\tau ; \Delta t)
E [ c ∗ ( τ 1 ; t ) c ( τ 2 ; t + Δ t ) ] = A c ( τ 1 ; Δ t ) δ [ τ 1 − τ 2 ] ≜ A c ( τ ; Δ t )
其中A c ( τ ; Δ t ) A_{c}(\tau ; \Delta t) A c ( τ ; Δ t ) τ = τ 1 = τ 2 \tau=\tau_1=\tau_2 τ = τ 1 = τ 2 Δ t \Delta t Δ t
定义scattering function:
A c ( τ , Δ t ) ⟷ S c ( τ , ρ ) = ∫ − ∞ ∞ A c ( τ , Δ t ) e − j 2 π ρ Δ t d Δ t A_c(\tau,\Delta t)\longleftrightarrow S_{c}(\tau, \rho)=\int_{-\infty}^{\infty} A_c(\tau, \Delta t) e^{-j 2 \pi \rho \Delta t}\ \mathrm{d} \Delta t
A c ( τ , Δ t ) ⟷ S c ( τ , ρ ) = ∫ − ∞ ∞ A c ( τ , Δ t ) e − j 2 π ρ Δ t d Δ t
散射函数描述了与信道相关的平均输出功率,是多径延迟τ \tau τ ρ \rho ρ
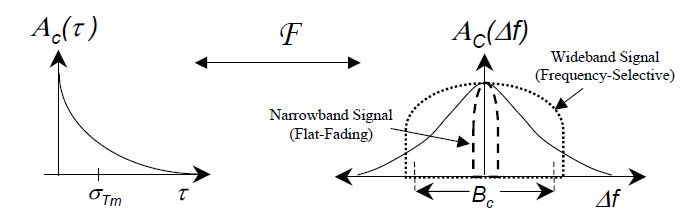
功率时延谱(power delay profile) :令A c ( τ , Δ t ) A_c(\tau,\Delta t) A c ( τ , Δ t ) Δ t = 0 \Delta t=0 Δ t = 0 A c ( τ ) = A c ( τ , 0 ) A_c(\tau)=A_c(\tau,0) A c ( τ ) = A c ( τ , 0 )
相干带宽(Coherence Bandwidth)
多普勒功率谱(Doppler Power Spectrum)与相干时间(Channel Coherence Time)
令A C ( Δ f , Δ t ) A_C(\Delta f,\Delta t) A C ( Δ f , Δ t ) Δ f = 0 \Delta f=0 Δ f = 0 A C ( Δ t ) A_C(\Delta t) A C ( Δ t )
S C ( ρ ) = ∫ − ∞ ∞ A C ( Δ t ) e − j 2 π ρ Δ t d Δ t S_{C}(\rho)=\int_{-\infty}^{\infty} A_{C}(\Delta t) e^{-j 2 \pi \rho \Delta t} d \Delta t
S C ( ρ ) = ∫ − ∞ ∞ A C ( Δ t ) e − j 2 π ρ Δ t d Δ t
多普勒功率谱(Doppler Power Spectrum)描述接收功率在多普勒频率ρ \rho ρ
Doppler spread(多普勒扩展):
∀ Δ ρ > B D , ∣ S C ( ρ ) ∣ ≈ 0 \forall \Delta \rho>B_D,|S_C(\rho)|\approx 0
∀ Δ ρ > B D , ∣ S C ( ρ ) ∣ ≈ 0
相干时间(Channel Coherence Time)T c T_c T c A C ( Δ t ) A_C(\Delta t) A C ( Δ t )
根据随机信号分析知识,
T c = ∫ 0 ∞ A C ( Δ t ) d Δ t T_c=\int_0^\infty A_C(\Delta t)\ d\Delta t
T c = ∫ 0 ∞ A C ( Δ t ) d Δ t
多普勒扩展和相干时间的关系:
B D ≈ 1 T c B_D\approx \frac 1{T_c}
B D ≈ T c 1
S c ( τ ; ρ ) = F Δ t F Δ f − 1 [ A C ( Δ f ; Δ t ) ] = ∫ − ∞ ∞ ∫ − ∞ ∞ A C ( Δ f ; Δ t ) e − j 2 π ρ Δ t e j 2 π τ Δ f d Δ t d Δ f S_{c}(\tau ; \rho)=\mathscr{F}_{\Delta t}\mathscr{F}_{\Delta f}^{-1}[ A_{C}(\Delta f ; \Delta t)]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} A_{C}(\Delta f ; \Delta t) e^{-j 2 \pi \rho \Delta t} e^{j 2 \pi \tau \Delta f} d \Delta t d \Delta f
S c ( τ ; ρ ) = F Δ t F Δ f − 1 [ A C ( Δ f ; Δ t ) ] = ∫ − ∞ ∞ ∫ − ∞ ∞ A C ( Δ f ; Δ t ) e − j 2 π ρ Δ t e j 2 π τ Δ f d Δ t d Δ f
通常情况下,时变脉冲响应信道模型对于简单的分析来说过于复杂。在这种情况下,可以使用宽带多径模型的离散时间近似值。这个离散时间模型是基于一个由孤立的点状散射体组成的物理传播环境。
c ( τ ; t ) = ∑ n = 0 N α n ( t ) e − j ϕ n ( t ) δ ( τ − τ n ( t ) ) c(\tau ; t)=\sum_{n=0}^{N} \alpha_{n}(t) e^{-j \phi_{n}(t)} \delta\left(\tau-\tau_{n}(t)\right)
c ( τ ; t ) = n = 0 ∑ N α n ( t ) e − j ϕ n ( t ) δ ( τ − τ n ( t ) )
给定t t t τ \tau τ T T T M M M M T ≥ σ T m MT\ge \sigma_{T_m} M T ≥ σ T m M M M M T MT M T T ≈ 1 B T\approx \frac 1B T ≈ B 1
随着时间的推移,用一连串的时间点配置数据刻画信道脉冲响应的变化。
多天线在无线系统中变得非常普遍。具有多天线的系统需要信道模型来体现信道的空间(到达角)和时间特性。
对于二维多径传播环境,接收天线或发射天线配备M M M
c ( τ , t ) = ∑ n = 0 N ( t ) α n ( t ) e − j ϕ n ( t ) a ˉ ( θ n ( t ) ) δ ( τ − τ n ( t ) ) c(\tau, t)=\sum_{n=0}^{N(t)} \alpha_{n}(t) e^{-j \phi_{n}(t)} \bar{a}\left(\theta_{n}(t)\right) \delta\left(\tau-\tau_{n}(t)\right)
c ( τ , t ) = n = 0 ∑ N ( t ) α n ( t ) e − j ϕ n ( t ) a ˉ ( θ n ( t ) ) δ ( τ − τ n ( t ) )
其中,a ˉ ( θ n ( t ) ) \bar{a}\left(\theta_{n}(t)\right) a ˉ ( θ n ( t ) )
ANDREA GOLDSMITH.WIRELESS COMMUNICATIONS .2005.
(美)Andrea Goldsmith著;杨鸿文,李卫东,郭文彬等译. 无线通信. 北京:人民邮电出版社, 2007.06.
陈伯孝. 雷达原理与系统(讲义). 西安电子科技大学, 2021.02.
![uniform scattering environment]()
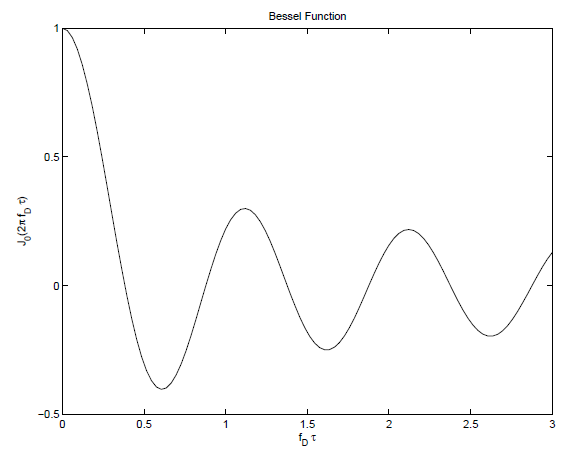
![零阶贝塞尔函数]()
![窄带信道中功率随距离变化]()
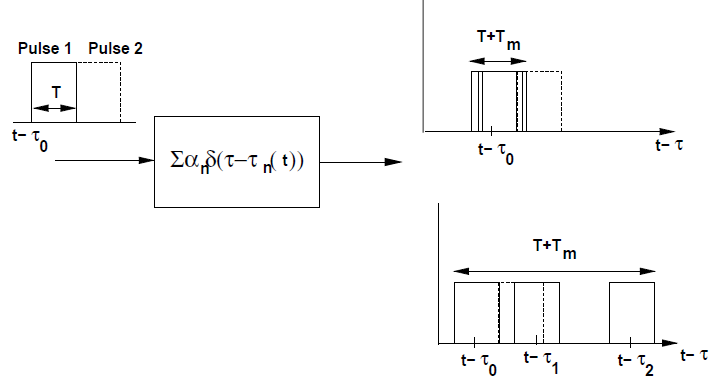
![fading]()