Wireless Communications (Andrea Goldsmith)学习笔记。
主要讲述 path loss (路径损耗) and shadowing (阴影衰弱)相对于距离对接收信号功率的影响。并考虑这两方面的影响建立信道模型。
Path loss is caused by dissipation of the power radiated by the transmitter as well as effects of the propagation channel. (be the same at a given transmit-receive distance)Shadowing is caused by obstacles between the transmitter and receiver that attenuate signal power through absorption, reflection, scattering, and diffraction. (When the attenuation is very strong, the signal is blocked)
大尺度传播效应和小尺度传播效应
large-scale propagation effects: occur over relatively large distances. e.g. variations due to path loss and shadowing
small-scale propagation effects: occurs over very short distances, on the order of the signal wavelength
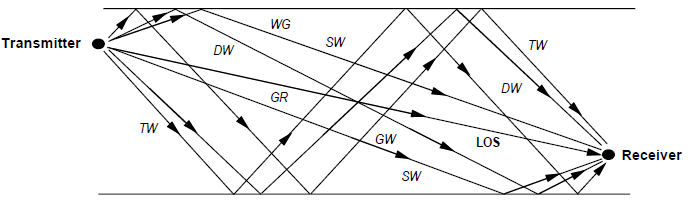
开发了一些近似方法来描述信号传播的特点,而不需要借助麦克斯韦方程。最常见的近似方法是使用 ray-tracing techniques (射线跟踪技术)。
transmitted signal:
s ( t ) = ℜ { u ( t ) e 2 π f c t } = x ( t ) cos ( 2 π f c t ) − y ( t ) sin ( 2 π f c t ) s(t)=\Re\left\{u(t)e^{2\pi f_c t}\right\}=x(t)\cos(2\pi f_ct)-y(t)\sin(2\pi f_c t)
s ( t ) = ℜ { u ( t ) e 2 π f c t } = x ( t ) cos ( 2 π f c t ) − y ( t ) sin ( 2 π f c t )
其中,信号 u ( t ) = x ( t ) + j y ( t ) u(t)=x(t)+jy(t) u ( t ) = x ( t ) + j y ( t ) B u B_u B u P u P_u P u P ( t ) = P u 2 P(t)=\frac{ P_u}{2} P ( t ) = 2 P u
received signal:
r ( t ) = ℜ { v ( t ) e j 2 π f c t } = ℜ { u ( t ) ∗ c ( t ) ⋅ e j 2 π f c t } r(t)=\Re{\left\{v(t)e^{j2\pi f_c t}\right\}}=\Re{\left\{u(t)*c(t)\cdot e^{j2\pi f_c t}\right\}}
r ( t ) = ℜ { v ( t ) e j 2 π f c t } = ℜ { u ( t ) ∗ c ( t ) ⋅ e j 2 π f c t }
其中,c ( t ) c(t) c ( t ) f D = v cos θ λ f_D=\frac{v\cos\theta}{\lambda} f D = λ v cos θ
由free-space path loss出发建立最基础的模型。由于处理RCS过于复杂,在本章中都是从ray tracing的角度来建立复杂模型分析问题的,包括two-ray model, 10-ray model进而推广到一般的general ray tracing。
P L = P t P r P_L=\frac{P_t}{P_r}
P L = P r P t
视距信道(LOS,line-of-sight)
接收信号
r ( t ) = ℜ { λ G l e − j 2 π d / λ 4 π d u ( t ) e j 2 π f c t } r(t)=\Re\left\{\frac{\lambda \sqrt{G_{l}} e^{-j 2 \pi d / \lambda}}{4 \pi d} u(t) e^{j 2 \pi f_{c} t}\right\}
r ( t ) = ℜ { 4 π d λ G l e − j 2 π d / λ u ( t ) e j 2 π f c t }
其中,G l \sqrt{G_l} G l e − j 2 π d / λ e^{-j 2 \pi d / \lambda} e − j 2 π d / λ d d d 功率是信号的平方。
注:这里G l \sqrt{G_l} G l F ( θ , ϕ ) F(\theta,\phi) F ( θ , ϕ ) D D D Friis传输方程 :
P R = P i ( λ 4 π r ) 2 D i D r P_R=P_i\left(\frac{\lambda}{4\pi r}\right)^2D_iD_r
P R = P i ( 4 π r λ ) 2 D i D r
上式是在满足极化匹配、共轭匹配和收发最大辐射方向对准时的表达式。在天线原理书后习题中也被写作
P R = P i ( λ 4 π r ) 2 G i G r P_R=P_i\left(\frac{\lambda}{4\pi r}\right)^2G_iG_r
P R = P i ( 4 π r λ ) 2 G i G r
显然这是在考虑天线效率情况下的Friis传输方程。注意到下面路径增益中将收发天线的增益看作是一样的也就是G l G_l G l
路径增益
P r P t = [ G l λ 4 π d ] 2 \frac {P_r}{P_t}=\left[\frac{\sqrt{G_l}\lambda}{4\pi d}\right]^2
P t P r = [ 4 π d G l λ ] 2
接收机接收功率随着收发天线之间距离d d d
当载波频率增加,接收功率下降。
自由空间路径损耗
P L dB = 10 lg P t P r = − 10 lg [ G l λ 4 π d ] 2 P_L\text{ dB}=10 \lg\frac{P_t}{P_r}=-10\lg\left[\frac{\sqrt{G_l}\lambda}{4\pi d}\right]^2
P L dB = 1 0 lg P r P t = − 1 0 lg [ 4 π d G l λ ] 2
multipath signal components:additional copies of the transmitted signal
multipath signal components相对于LOS信道的接收信号有功率衰减,延时,相移和/或频移。
射线追踪技术通过将波面表示为简单的粒子来逼近电磁波的传播。
smallest when the receiver is many wavelengths from the nearest scatterer, and all the scatterers are large relative to a wavelength and fairly smooth.射线跟踪不能很好的反映多径时延扩展(delay spread)
当单一地面反射主导多径效应时,采用Two-Ray Model。
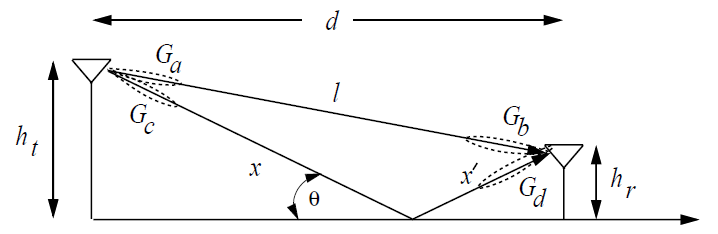
由LOS路径的接受的直射信号和经过x , x ′ x,x' x , x ′
r 2 ray ( t ) = ℜ { λ 4 π [ G l u ( t ) e − j 2 π l / λ l + R G r u ( t − τ ) e − j 2 π ( x + x ′ ) / λ x + x ′ ] e j 2 π f c t } r_{2 \text {ray }}(t)=\Re\left\{\frac{\lambda}{4 \pi}\left[\frac{\sqrt{G_{l}} u(t) e^{-j 2 \pi l / \lambda}}{l}+\frac{R \sqrt{G_{r}} u(t-\tau) e^{-j 2 \pi\left(x+x^{\prime}\right) / \lambda}}{x+x^{\prime}}\right] e^{j 2 \pi f_{c} t}\right\}
r 2 ray ( t ) = ℜ { 4 π λ [ l G l u ( t ) e − j 2 π l / λ + x + x ′ R G r u ( t − τ ) e − j 2 π ( x + x ′ ) / λ ] e j 2 π f c t }
进一步假设接收信号相对于delay spread(τ \tau τ τ ≪ B u − 1 \tau\ll B_u^{-1} τ ≪ B u − 1 u ( t ) ≈ u ( t − τ ) u(t)\approx u(t-\tau) u ( t ) ≈ u ( t − τ )
P r = P t [ λ 4 π ] 2 ∣ G l l + R G r e − j Δ ϕ x + x ′ ∣ 2 P_{r}=P_{t}\left[\frac{\lambda}{4 \pi}\right]^{2}\left|\frac{\sqrt{G_{l}}}{l}+\frac{R \sqrt{G_{r}} e^{-j \Delta \phi}}{x+x^{\prime}}\right|^{2}
P r = P t [ 4 π λ ] 2 ∣ ∣ ∣ ∣ l G l + x + x ′ R G r e − j Δ ϕ ∣ ∣ ∣ ∣ 2
其中,Δ ϕ = 2 π ( x + x ′ − l ) / λ \Delta\phi=2\pi (x+x'-l)/\lambda Δ ϕ = 2 π ( x + x ′ − l ) / λ
当d d d x + x ′ ≈ l ≈ d , θ ≈ 0 , G l ≈ G r , R = − 1 x+x^{\prime} \approx l \approx d, \theta \approx 0, G_{l} \approx G_{r},R=-1 x + x ′ ≈ l ≈ d , θ ≈ 0 , G l ≈ G r , R = − 1
P r ≈ [ λ G l 4 π d ] 2 [ 4 π h t h r λ d ] 2 P t = [ G l h t h r d 2 ] 2 P t P_{r} \approx\left[\frac{\lambda \sqrt{G_{l}}}{4 \pi d}\right]^{2}\left[\frac{4 \pi h_{t} h_{r}}{\lambda d}\right]^{2} P_{t}=\left[\frac{\sqrt{G_{l}} h_{t} h_{r}}{d^{2}}\right]^{2} P_{t}
P r ≈ [ 4 π d λ G l ] 2 [ λ d 4 π h t h r ] 2 P t = [ d 2 G l h t h r ] 2 P t
一些说明:
接收功率与λ \lambda λ
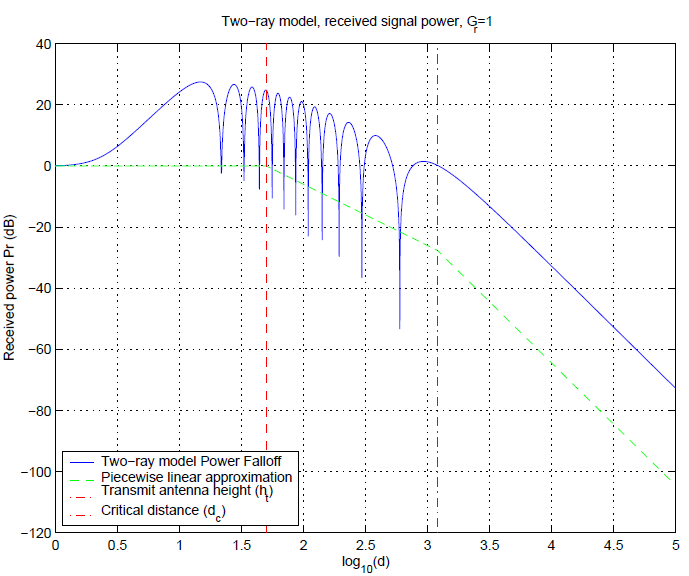
近距离(d < h t d<h_t d < h t 1 d 2 + h t 2 \frac {1}{d^2+h_t^2} d 2 + h t 2 1
远距离(h t < d < d c h_t<d<d_c h t < d < d c d − 4 d^{-4} d − 4
d > d c d>d_c d > d c d c d_c d c d c d_c d c d c d_c d c Δ ϕ = π \Delta \phi=\pi Δ ϕ = π d c = 4 h t h r λ d_c=\frac{4h_th_r}{\lambda} d c = λ 4 h t h r
蜂窝系统(cellular systems)中传播很少符合two-ray model。
当单一路径反射超过三次可以被忽略。后向反射也可以被忽略。
Ten-Ray Model下的接收信号为
r 10 ray ( t ) = ℜ { λ 4 π [ G l u ( t ) e − j 2 π l / λ l + ∑ i = 1 9 R i G x i u ( t − τ i ) e − j 2 π x i / λ x i ] e j 2 π f c t } r_{10 \text {ray }}(t)=\Re\left\{\frac{\lambda}{4 \pi}\left[\frac{\sqrt{G_{l}} u(t) e^{-j 2 \pi l / \lambda}}{l}+\sum_{i=1}^{9} \frac{R_{i} \sqrt{G_{x_{i}}} u\left(t-\tau_{i}\right) e^{-j 2 \pi x_{i} / \lambda}}{x_{i}}\right] e^{j 2 \pi f_{c} t}\right\}
r 1 0 ray ( t ) = ℜ { 4 π λ [ l G l u ( t ) e − j 2 π l / λ + i = 1 ∑ 9 x i R i G x i u ( t − τ i ) e − j 2 π x i / λ ] e j 2 π f c t }
进一步假设接收信号相对于delay spread(τ \tau τ u ( t ) ≈ u ( t − τ ) u(t)\approx u(t-\tau) u ( t ) ≈ u ( t − τ )
P r = P t [ λ 4 π ] 2 ∣ G l l + ∑ i = 1 9 R i G x i e − j Δ ϕ i x i ∣ 2 P_{r}=P_{t}\left[\frac{\lambda}{4 \pi}\right]^{2}\left|\frac{\sqrt{G_{l}}}{l}+\sum_{i=1}^{9} \frac{R_{i} \sqrt{G_{x_{i}}} e^{-j \Delta \phi_{i}}}{x_{i}}\right|^{2}
P r = P t [ 4 π λ ] 2 ∣ ∣ ∣ ∣ ∣ l G l + i = 1 ∑ 9 x i R i G x i e − j Δ ϕ i ∣ ∣ ∣ ∣ ∣ 2
Ten-Ray Model的接收功率随d 2 d^{2} d 2
对于GRT模型,建筑物参数(高度、位置和介电性质)以及发射机和接收机相对于建筑物的位置必须准确确定。
一般来说,由于绕射(diffraction)和散射(scattering)的损耗很大,所以在接收信号中起主导作用的十LOS信号和反射信号。
diffraction(绕射)分量可由Fresnel knife edge diffraction model求得,接收信号为
r ( t ) = ℜ { L ( v ) G d u ( t − τ ) e − j 2 π ( d + d ′ ) / λ e j 2 π f c t } r(t)=\Re\left\{L(v) \sqrt{G_{d}} u(t-\tau) e^{-j 2 \pi\left(d+d^{\prime}\right) / \lambda} e^{j 2 \pi f_{c} t}\right\}
r ( t ) = ℜ { L ( v ) G d u ( t − τ ) e − j 2 π ( d + d ′ ) / λ e j 2 π f c t }
其中,G d \sqrt{G_d} G d τ = Δ d c \tau=\frac{\Delta d}{c} τ = c Δ d
scattered ray(散射)分量可有双基地雷达方程(bistatic radar equation)获得,接收信号为
结合上述各种分量的影响,假设有一个LOS路径,N r N_r N r N d N_d N d N s N_s N s
r total ( t ) = ℜ { [ λ 4 π ] [ G l u ( t ) e j 2 π l / λ l + ∑ i = 1 N r R x i G x i u ( t − τ i ) e − j 2 π x i / λ x i + ∑ j = 1 N d L j ( v ) G d j u ( t − τ j ) e − j 2 π ( d j + d j ′ ) / λ + ∑ k = 1 N s G s k σ k u ( t − τ k ) e j 2 π ( s k + s k ′ ) / λ s k s k ′ ] e j 2 π f c t } \begin{aligned}
r_{\text {total }}(t) &=\Re\left\{\left[ \frac { \lambda } { 4 \pi } \right] \left[\frac{\sqrt{G_{l}} u(t) e^{j 2 \pi l / \lambda}}{l}+\sum_{i=1}^{N_{r}} \frac{R_{x_{i}} \sqrt{G_{x_{i}}} u\left(t-\tau_{i}\right) e^{-j 2 \pi x_{i} / \lambda}}{x_{i}}\right.\right.\\
&+\sum_{j=1}^{N_{d}} L_{j}(v) \sqrt{G_{d_{j}}} u\left(t-\tau_{j}\right) e^{-j 2 \pi\left(d_{j}+d_{j}^{\prime}\right) / \lambda} \\
&\left.\left.+\sum_{k=1}^{N_{s}} \frac{\sqrt{G_{s_{k}} \sigma_{k}} u\left(t-\tau_{k}\right) e^{j 2 \pi\left(s_{k}+s_{k}^{\prime}\right) / \lambda}}{s_{k} s_{k}^{\prime}}\right] e^{j 2 \pi f_{c} t}\right\}
\end{aligned}
r total ( t ) = ℜ { [ 4 π λ ] [ l G l u ( t ) e j 2 π l / λ + i = 1 ∑ N r x i R x i G x i u ( t − τ i ) e − j 2 π x i / λ + j = 1 ∑ N d L j ( v ) G d j u ( t − τ j ) e − j 2 π ( d j + d j ′ ) / λ + k = 1 ∑ N s s k s k ′ G s k σ k u ( t − τ k ) e j 2 π ( s k + s k ′ ) / λ ] e j 2 π f c t }
如果其传播路径被建筑物或其他物体阻挡,任何一个多径分量都可能有一个额外的衰减系数。
local mean received power(P ˉ r \bar P_r P ˉ r
为了消除多径效应,路径损耗的经验测量通常将其接收功率测量值和相应的路径损耗在给定距离上的几个波长上求平均值。这个平均路径损耗称为距离d d d 本地平均衰减(LMA) ,由于自由空间的路径损耗和信号障碍物的影响,一般会随着d d d
The Okumura Model: One of the most common models for signal prediction in large urban macrocells is the Okumura model . This model is applicable over distances of 1-100 km and frequency ranges of 150-1500 MHz. The base station heights30-100 m , the upper end of which is higher than typical base stations today
P L ( d ) d B = L ( f c , d ) + A m u ( f c , d ) − G ( h t ) − G ( h r ) − G A R E A P_{L}(d) \mathrm{dB}=L\left(f_{c}, d\right)+A_{m u}\left(f_{c}, d\right)-G\left(h_{t}\right)-G\left(h_{r}\right)-G_{A R E A}
P L ( d ) d B = L ( f c , d ) + A m u ( f c , d ) − G ( h t ) − G ( h r ) − G A R E A
Hata Model: This empirical model simplifies calculation of path loss since it is a closed-form formula and is not based on empirical curves for the different parameters. the same range of frequencies, 150-1500 MHz.
P L , u r b a n ( d ) d B = 69.55 + 26.16 log 10 ( f c ) − 13.82 log 10 ( h t ) − a ( h r ) + ( 44.9 − 6.55 log 10 ( h t ) ) log 10 ( d ) P_{L, u r b a n}(d) \mathrm{dB}=69.55+26.16 \log _{10}\left(f_{c}\right)-13.82 \log _{10}\left(h_{t}\right)-a\left(h_{r}\right)+\left(44.9-6.55 \log _{10}\left(h_{t}\right)\right) \log _{10}(d)
P L , u r b a n ( d ) d B = 6 9 . 5 5 + 2 6 . 1 6 log 1 0 ( f c ) − 1 3 . 8 2 log 1 0 ( h t ) − a ( h r ) + ( 4 4 . 9 − 6 . 5 5 log 1 0 ( h t ) ) log 1 0 ( d )
COST 231 Extension to Hata Model: The Hata model was extended to 2 GHz .
P L , u r b a n ( d ) d B = 46.3 + 33.9 log 10 ( f c ) − 13.82 log 10 ( h t ) − a ( h r ) + ( 44.9 − 6.55 log 10 ( h t ) ) log 10 ( d ) + C M P_{L, u r b a n}(d) \mathrm{dB}=46.3+33.9 \log _{10}\left(f_{c}\right)-13.82 \log _{10}\left(h_{t}\right)-a\left(h_{r}\right)+\left(44.9-6.55 \log _{10}\left(h_{t}\right)\right) \log _{10}(d)+C_{M}
P L , u r b a n ( d ) d B = 4 6 . 3 + 3 3 . 9 log 1 0 ( f c ) − 1 3 . 8 2 log 1 0 ( h t ) − a ( h r ) + ( 4 4 . 9 − 6 . 5 5 log 1 0 ( h t ) ) log 1 0 ( d ) + C M
This model is referred to as the COST 231 extension to the Hata model, and is restrictedf c f_c f c h t h_t h t h r h_r h r d d d
Piecewise Linear (Multi-Slope) Model
Indoor Attenuation Factors: it is difficult to find generic models that can be accurately applied to determine empirical path loss in a specific indoor setting.
对于一般的衰减分析,可以使用路径损耗的简化模型:
P r = P t K [ d 0 d ] γ P_r=P_tK\left[\frac{d_0}{d}\right]^\gamma
P r = P t K [ d d 0 ] γ
用分贝表示
P r d B m = P t d B m + K d B − 10 γ log 10 [ d d 0 ] P_{r} \mathrm{dBm}=P_{t} \mathrm{dBm}+K \mathrm{~dB}-10 \gamma \log _{10}\left[\frac{d}{d_{0}}\right]
P r d B m = P t d B m + K d B − 1 0 γ log 1 0 [ d 0 d ]
其中,K K K d 0 d_0 d 0 γ \gamma γ
K K K K < 1 K<1 K < 1 d 0 d_0 d 0
K d B = 20 log 10 λ 4 π d 0 K \mathrm{~dB}=20 \log _{10} \frac{\lambda}{4 \pi d_{0}}
K d B = 2 0 log 1 0 4 π d 0 λ
这里假设天线效率η A \eta_A η A G = η A D G=\eta_A D G = η A D D D D
对于全向辐射的假想元:
D = 4 π ∫ o 2 π ∫ 0 π sin θ d θ d ϕ = 1 = 0 dBi D=\frac{4\pi}{\int_o^{2\pi}\int_{0}^{\pi}\sin \theta \mathrm{d}\theta\mathrm{d}\phi}=1=0\text{ dBi}
D = ∫ o 2 π ∫ 0 π sin θ d θ d ϕ 4 π = 1 = 0 dBi
代入路径增益的表达式即为上式。
γ \gamma γ γ \gamma γ
F ( γ ) = ∑ i = 1 n [ M measured − M model ] 2 F(\gamma)=\sum_{i=1}^{n}\left[M_\text{measured}-M_\text{model}\right]^2
F ( γ ) = i = 1 ∑ n [ M measured − M model ] 2
其中M measured M_\text{measured} M measured 10 lg P r P t dB 10\lg\frac{P_r}{P_t} \text{ dB} 1 0 lg P t P r dB M model M_\text{model} M model 10 lg P r P t dB = K d B − 10 γ log 10 [ d d 0 ] 10\lg\frac{P_r}{P_t} \text{ dB}=K \mathrm{~dB}-10 \gamma \log _{10}\left[\frac{d}{d_{0}}\right] 1 0 lg P t P r dB = K d B − 1 0 γ log 1 0 [ d 0 d ] F ( γ ) F(\gamma) F ( γ )
∂ F ( γ ) γ = 0 → γ \frac{\partial F(\gamma)}{\gamma}=0\to\gamma
γ ∂ F ( γ ) = 0 → γ
也可以通过经验数据获得:
Environment
γ range
Urban macrocells
3.7-6.5
Urban microcells
2.7-3.5
Office Building (same floor)
1.6-3.5
Office Building (multiple floors)
2-6
Store
1.8-2.2
Factory
1.6-3.3
Home
3
通过无线信道传输的信号通常会因为信号路径中物体的阻挡而发生随机变化,从而引起给定距离内接收功率的随机变化。由于参数是未知的,所以只能通过统计模型来表征这种随机变化。
最常用来描述这种加性衰减的模型是log-normal shadowing。
在log-normal shadowing model中,发射接收功率比ψ = P t P r \psi=\frac{P_t}{P_r} ψ = P r P t
p ( ψ ) = ξ 2 π σ ψ dB ψ exp [ − ( 10 log 10 ψ − μ ψ dB ) 2 2 σ ψ dB 2 ] , ψ > 0 p(\psi)=\frac{\xi}{\sqrt{2 \pi} \sigma_{\psi_\text{dB}} \psi} \exp \left[-\frac{\left(10 \log _{10} \psi-\mu_{\psi_\text{dB}}\right)^{2}}{2 \sigma_{\psi_\text{dB}}^{2}}\right], \psi>0
p ( ψ ) = 2 π σ ψ dB ψ ξ exp [ − 2 σ ψ dB 2 ( 1 0 log 1 0 ψ − μ ψ dB ) 2 ] , ψ > 0
其中,ξ = 10 ln 10 \xi=\frac{10}{\ln 10} ξ = ln 1 0 1 0 ψ dB = 10 lg ψ \psi_\text{dB}=10\lg\psi ψ dB = 1 0 lg ψ μ ψ dB , σ ψ dB \mu_{\psi_\text{dB}},\sigma_{\psi_\text{dB}} μ ψ dB , σ ψ dB ψ dB \psi_\text{dB} ψ dB
ψ = P t P r \psi=\frac{P_t}{P_r} ψ = P r P t
注意:在经验路径损耗模型中,由于无法拆分,μ ψ dB \mu_{\psi_\text{dB}} μ ψ dB
通常我们对测量值的分贝值取平均来确定平均的路径损耗和方差。
假设Shadowing ψ ( d ) \psi(d) ψ ( d ) δ \delta δ
A ( δ ) = E [ ( ψ d B ( d ) − μ ψ d B ) ( ψ d B ( d + δ ) − μ ψ d B ) ] = σ ψ d B 2 ρ D δ / D A(\delta)=\mathrm{E}\left[\left(\psi_{d B}(d)-\mu_{\psi_{d B}}\right)\left(\psi_{d B}(d+\delta)-\mu_{\psi_{d B}}\right)\right]=\sigma_{\psi_{d B}}^{2} \rho_{D}^{\delta / D}
A ( δ ) = E [ ( ψ d B ( d ) − μ ψ d B ) ( ψ d B ( d + δ ) − μ ψ d B ) ] = σ ψ d B 2 ρ D δ / D
其中,ρ D \rho_D ρ D D D D
假设固定D = X c D=X_c D = X c ρ D = 1 e \rho_D=\frac 1e ρ D = e 1
A ( δ ) = σ ψ dB 2 e − δ / X c A(\delta)=\sigma^2_{\psi_\text{dB}}e^{-\delta/X_c}
A ( δ ) = σ ψ dB 2 e − δ / X c
其中,X c X_c X c 1 e \frac 1e e 1
当用户以速度v v v δ = v τ \delta=v\tau δ = v τ τ \tau τ
综合上述路径损耗的简化模型和对数正态分布的阴影衰减模型,可得接收发射功率比为
P r P t (dB) = 10 log 10 K − 10 γ log 10 d d 0 − ψ d B \frac{P_{r}}{P_{t}}\text{(dB)}=10 \log _{10} K-10 \gamma \log _{10} \frac{d}{d_{0}}-\psi_{d B}
P t P r (dB) = 1 0 log 1 0 K − 1 0 γ log 1 0 d 0 d − ψ d B
ψ dB ∼ N ( 0 , σ ψ dB 2 ) \psi_\text{dB}\sim N(0,\sigma^2_{\psi_\text{dB}}) ψ dB ∼ N ( 0 , σ ψ dB 2 ) 路径损耗随着lg d \lg d lg d 10 γ dB/decade 10\gamma\text{ dB/decade} 1 0 γ dB/decade
阴影衰减导致的变化非常快,和去相关距离X c X_c X c
无线通信中有目标允许最小接收功率P min P_{\min} P min
中断概率(Outage Probability):在距离d d d P r ( d ) P_r(d) P r ( d ) P min P_{\min} P min
p out ( P min , d ) = p ( P r ( d ) < P min ) p_\text{out}(P_{\min},d)=p\left(P_r(d)<P_{\min}\right)
p out ( P min , d ) = p ( P r ( d ) < P min )
对于路径损耗的简化模型和对数正态分布的阴影衰减模型,上式可写为
p ( P r ( d ) ≤ P min ) = 1 − Q ( P min − ( P t + 10 log 10 K − 10 γ log 10 ( d / d 0 ) ) σ ψ dB ) p\left(P_{r}(d) \leq P_{\min }\right)=1-Q\left(\frac{P_{\min }-\left(P_{t}+10 \log _{10} K-10 \gamma \log _{10}\left(d / d_{0}\right)\right)}{\sigma_{\psi_\text{dB}}}\right)
p ( P r ( d ) ≤ P min ) = 1 − Q ( σ ψ dB P min − ( P t + 1 0 log 1 0 K − 1 0 γ log 1 0 ( d / d 0 ) ) )
其中,
Q ( z ) ≜ p ( x > z ) = ∫ z ∞ 1 2 π e − y 2 / 2 d y = 1 2 e r f c ( z 2 ) Q(z) \triangleq p(x>z)=\int_{z}^{\infty} \frac{1}{\sqrt{2 \pi}} e^{-y^{2} / 2} d y=\frac 12\mathrm{erfc}\left(\frac{z}{\sqrt{2}}\right)
Q ( z ) ≜ p ( x > z ) = ∫ z ∞ 2 π 1 e − y 2 / 2 d y = 2 1 e r f c ( 2 z )
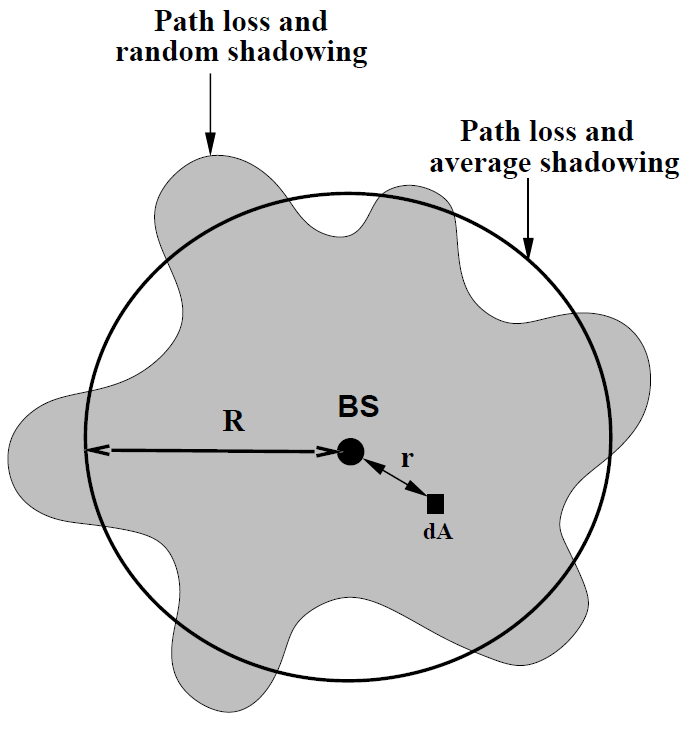
考虑路径损耗和平均的阴影衰减,等功率线是以基站(Base station, BS)为圆心的圆。而考虑路径损耗和随机的阴影损耗,等功率线就变成一个不规则图形。
不能保证在cell的边界上的人接收相同的功率量级,两种解决方式
transmit extra power to insure users affected by shadowing receive their minimum required powerP min P_{\min} P min
some users within the cell will not meet their minimum received power requirement.
outage probability of the cell(小区中的中断概率):小区内未达到最低功率要求的面积百分比
p out cell = 1 − C p_\text{out}^\text{cell}=1-C
p out cell = 1 − C
C = 1 π R 2 ∫ cell area P A d A = 1 π R 2 ∫ 0 2 π ∫ 0 R P A r d r d θ C=\frac{1}{\pi R^{2}} \int_{\text {cell area }} P_{A} d A=\frac{1}{\pi R^{2}} \int_{0}^{2 \pi} \int_{0}^{R} P_{A} r d r d \theta
C = π R 2 1 ∫ cell area P A d A = π R 2 1 ∫ 0 2 π ∫ 0 R P A r d r d θ
其中,P A P_A P A d A \mathrm{d}A d A P A = E [ 1 [ P r ( r ) > P min in d A ] ] P_{A}=\mathrm{E}\left[1\left[P_{r}(r)>P_{\min } \text { in } d A\right]\right] P A = E [ 1 [ P r ( r ) > P min in d A ] ] 1 [ ∙ ] 1[\bullet] 1 [ ∙ ]
对于路径损耗的简化模型和对数正态分布的阴影衰减模型,有
p ( P r ( r ) > P min ) = 1 − p out ( P min , r ) p(P_{r}(r)>P_{\min })=1-p_\text{out}(P_{\min},r)
p ( P r ( r ) > P min ) = 1 − p out ( P min , r )
小区中接收功率低于P min P_{\min} P min
若目标最小接收功率P min P_{\min} P min P ˉ r \bar P_r P ˉ r
在整理的时候,真的发现好多和《天线原理》和《雷达原理与系统》交叉的内容。
ANDREA GOLDSMITH.WIRELESS COMMUNICATIONS .2005.
(美)Andrea Goldsmith著;杨鸿文,李卫东,郭文彬等译. 无线通信. 北京:人民邮电出版社, 2007.06.
魏文元等编. 天线原理. 北京:国防工业出版社, 1985.06.
无线通信学习笔记(二) 大尺度路径损耗.https://www.jianshu.com/p/5e9141e6cd76
![Received Power versus Distance for Two-Ray Model]()