【无监督学习】聚类算法——K-means

1聚类任务

1.1 无监督学习概述

机器学习一般包括监督学习、无监督学习、强化学习。有时候还包括半监督学习、主动学习。

1.1.1 监督学习与无监督学习

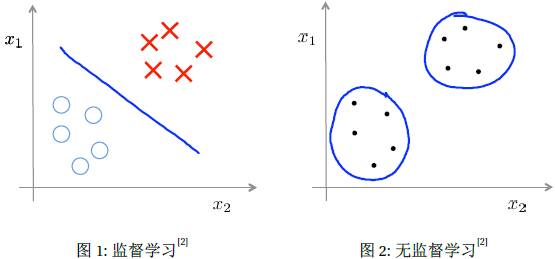
监督学习（Supervised learning） 监督学习（Supervised learning）是指从标注数据中学习预测模型的机器学习问题。监督学习的本质是从学习输入到输出的映射的统计规律。

$T=\{(\boldsymbol{x}_1,\boldsymbol{y}_1),(\boldsymbol{x}_2,\boldsymbol{y}_2),\cdots,(\boldsymbol{x}_m,\boldsymbol{y}_m)\}$

无监督学习（Unsupervised learning） 无监督学习（Unsupervised learning）是指从无标注数据中学习数据的统计规律。目标是通过对无标记的训练样本的学习来解释数据的内在性质及规律，为进一步的数据分析提供基础。主要包括聚类、降维、概率估计。无监督学习可以用于数据分析获监督学习的前处理。

$T=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_m\}$

1.1.2 聚类的引入

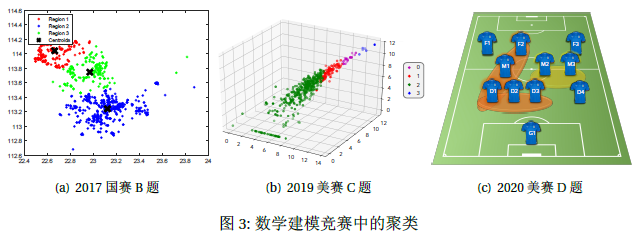
在数学建模竞赛中，会遇到不少类似这样的问题，比如拍照定价给城市分类(2017国赛B题)，美国阿片危机的城市(2019美赛C题，是一个三维图)，球员之间联系的紧密性研究(2020美赛D题)等，这些都是明显的聚类问题。

我们再举几个平时生活的例子，比如市场消费调研，社交网络分析，衣服尺码分布等等，这些问题所给出的样本，不像监督学习问题中的房价预测等问题。上述例子并没有带标签，而我们就把这样没有带标签的样本进行算法学习，由参数体现出的分类情况称为聚类，也就是Clustering。

聚类(Clustering)与簇(Cluster)

• 聚类试图将数据集中的样本划分为若干个通常是不相交的子集；

• 每个子集被称为一个"簇"。

聚类既能作为一个单独过程，用于寻找数据内在的分布结构，也可作为分类等其他学习任务的前驱过程。

1.2 预备知识------距离计算

距离计算

在聚类中，我们要将样本集划分为若干个互不相交的自己，即样本簇。那么什么样的聚类效果比较好呢？从直观上来说，我们希望"物以类聚"，即同一个簇的样本尽可能彼此相似，不同簇的样本尽可能地不同。换言之，聚类结果中的"簇内相似度"(intra-cluster similarity)高，而"簇间相似度"(inter-cluster similarity)低。

不论是聚类结果中的"簇内相似度"(intra-cluster similarity)还是"簇间相似度"(inter-cluster similarity)，我们都可以用距离$\mathrm{dist}$这个参量来定义。这里我只介绍为最基本的连续样本的几个"距离度量"。

闵可夫斯基距离(Minkowski distance)

$\mathrm{dist}_{mk}(\boldsymbol{x}_i,\boldsymbol{x}_j)=\left(\sum_{u=1}^n|x_{iu}-x_{ju}|^p\right)^{\frac{1}{p}}$

闵可夫斯基距离其实就是$\boldsymbol{x}_i-\boldsymbol{x}_j$的$\mathrm{L}_p$范数$||\boldsymbol{x}_i-\boldsymbol{x}_j||_p$

欧氏距离(Euclidean distance)

$\mathrm{dist}_{ed}(\boldsymbol{x}_i,\boldsymbol{x}_j)=||\boldsymbol{x}_i-\boldsymbol{x}_j||_2=\sqrt{\sum_{u=1}^n|x_{iu}-x_{ju}|^2}$

我们可以看出 闵可夫斯基距离其实就是$\boldsymbol{x}_i-\boldsymbol{x}_j$的$\mathrm{L}_p$范数，而当$p=2$时，就退化为了欧氏距离；而当$p=1$时，就退化为曼哈顿距离。

2 K-means算法概览

2.1 K-means算法的形象化理解

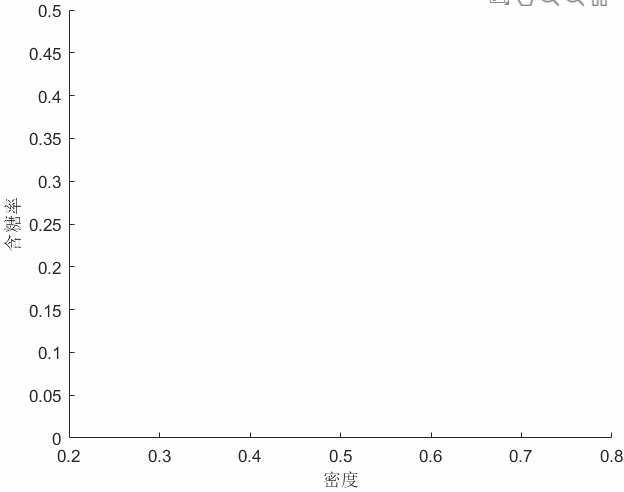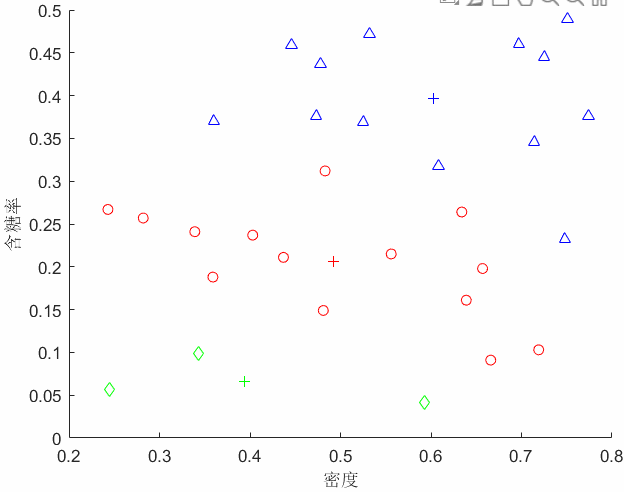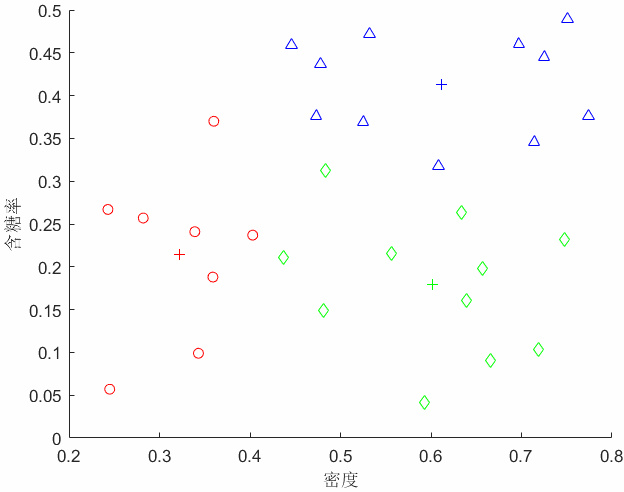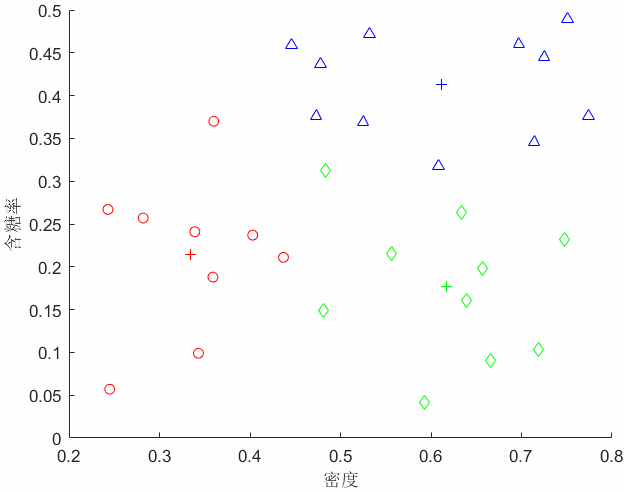
我们先来形象的理解一下K-means算法的流程是怎样的（动图）。假设我有一个无标签的数据集，然后我想把它分成3个簇。我们下面一步一步来理解一下这个过程。

1. 随机选择三个点------聚类中心（均值向量）；（我想把这些样本分成3个簇，K-means是一个迭代算法）

2. 第一个是簇分配：我们会遍历图上的每一个样本点，找到每个样本点距离最近的聚类中心，将样本点的颜色染成聚类中心的颜色，换言之分配给三个聚类中心；

3. 第二个是移动聚类中心：接着我们计算所有相同颜色的点的均值向量（质心），将开始的聚类中心移动到我们计算的均值向量处；就变成了这个图。

4. 我们反复操作这个迭代的过程，得到了最后的聚类结果。下面不管我们在怎么去迭代得到的都是这样的结果了。

2.2 K-means算法初步

2.2.1 算法的基本流程

输入

• $K$：簇的总数
• 样本集$D=\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_m\}$

首先，我们来看一看K-means 算法有哪些输出，一个是簇的总数，也就是说你最后想
要得到多少个簇；另一个就是我们的样本集，值得注意的是这个样本集是不带标签的。

下面我们来看一看算法的流程：

1. Initialization: 初始化聚类中心（均值向量）； 从刚刚的图形中，我们可以看出在最开始我们需要根据我们需要的聚类的个数$K$选择相应个数的聚类中心。这个操作我们称之为"初始化"(Initialization)。至于如何初始化，我们会在第三部分谈到。

2. **Cluster assignment: 簇分配；**第二个操作便是K-means算法的最重要的的两个操作之一------"簇分配"了，在这个步骤中，我们遍历数据集中的所有样本点，找到离每个点最近的聚类中心，将第$i$个样本分配给簇，并将簇的索引(Index)保存到变量$c_i$中。这个分配过程，我们可以理解为将每个样本点染色。

3. **Move centroid: 移动聚类中心（均值向量）；**为了让我们的K-means算法"运动"起来，我们势必将聚类中心也进行移动。那么如何移动呢？我们在这边先给出结论------我们将所有聚类中心移动到簇中所有点的质心处，即计算所有样本点向量的均值向量。正因如此，我们将聚类中心的位置用均值向量$\boldsymbol{\mu}_j$来表示。

4. **Iteration: 迭代；**最后一个操作，既然我们通过移动聚类中心，使得K-means算法"运动"起来。那么"聚类"，“聚类”，我们最终需要的是各个样本点之间的关系。我们有需要让样本点们重新染色，重新分配到上一步移动过的聚类中心去了。如此循环往复的过程便是"迭代"。既然是迭代必定会有一个结束条件------一般有两种：一是，针对小样本集来说，均值向量不再发生移动便为结束；二是，对于上千上万的数据，设置一个最大迭代次数来终止这个迭代过程。但是这个解是个最优解吗？很显然这并不一定，这很可能只是个局部最优解。这个问题，我会在第三部分中继续讨论。

这里我还给出了一个算法流程图，其中第1行就是对聚类中心进行初始化；在第4-7行和8-13行分别对于当前数据进行簇分配和移动聚类中心；2-14行这个总体过程是一个迭代的过程；当迭代更新后的聚类结果保持不见，则输出簇划分。

2.3 西瓜数据集4.0例

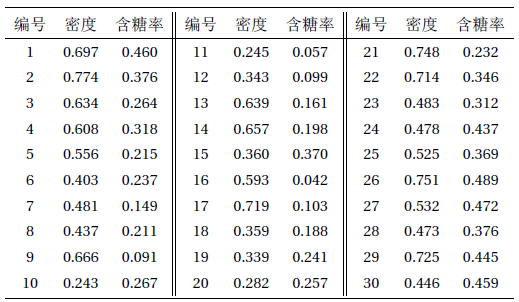
下面，我们以周志华老师编写的《机器学习》上的一个西瓜数据集4.0为例来演示K-means算法的学习过程。为了方便需要，我们将编号为$i$的样本成为$\boldsymbol{x}_i$，$\boldsymbol{x}_i$是一个包含"密度"和"含糖率"两属性值的二维向量。

2.3.1 初始化聚类中心（均值向量）(Initialization)

假设聚类簇的个数$K=3$，算法开始时随机选取三个样本$\boldsymbol{x}_6$,$\boldsymbol{x}_{12}$,$\boldsymbol{x}_{24}$作为初始均值向量，即

$\boldsymbol{\mu}_1=(0.403;0.237),\quad \boldsymbol{\mu}_2=(0.343;0.099),\quad \boldsymbol{\mu}_3=(0.478;0.437).$

2.3.2 簇分配(Cluster assignment)

考察样本$\boldsymbol{x}_1=(0.697;0.460)$，它与当前均值向量$\boldsymbol{\mu}_1,\boldsymbol{\mu}_2,\boldsymbol{\mu}_3$的距离分别为0.369, 0.506, 0.220，因此$\boldsymbol{x}_1$被划入簇$C_3$中。这里我们计算的都是欧氏距离，即$\mathrm{L}_2$范数。 类似的，对数据集中的所有样本进行考察，可得当前的簇划分为

$\begin{aligned} C_1=&\{\boldsymbol{x}_3, \boldsymbol{x}_5, \boldsymbol{x}_6, \boldsymbol{x}_7, \boldsymbol{x}_8, \boldsymbol{x}_9, \boldsymbol{x}_{10}, \boldsymbol{x}_{13}, \boldsymbol{x}_{14}, \boldsymbol{x}_{17}, \boldsymbol{x}_{18}, \boldsymbol{x}_{19}, \boldsymbol{x}_{20}, \boldsymbol{x}_{23}\};\\ C_2=&\{ \boldsymbol{x}_{11}, \boldsymbol{x}_{12}, \boldsymbol{x}_{16}\};\\ C_3=&\{\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_4, \boldsymbol{x}_{15}, \boldsymbol{x}_{21}, \boldsymbol{x}_{22}, \boldsymbol{x}_{24}, \boldsymbol{x}_{25}, \boldsymbol{x}_{26}, \boldsymbol{x}_{27}, \boldsymbol{x}_{28}, \boldsymbol{x}_{29}, \boldsymbol{x}_{30}\};\\ \end{aligned}$

我们将这30个样本点染上相应聚类中心的颜色。

2.3.3 移动聚类中心（均值向量）(Move Centroid)

于是我们从$C_1,\ C_2,\ C_3$中计算出新的均值向量，即

$\boldsymbol{\mu}_1=(0.493;0.207),\quad \boldsymbol{\mu}_2=(0.394;0.066),\quad \boldsymbol{\mu}_3=(0.602;0.396).$

然后将相应的聚类中心移动到更新的均值向量处。

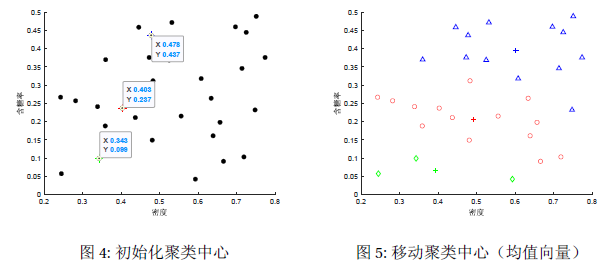
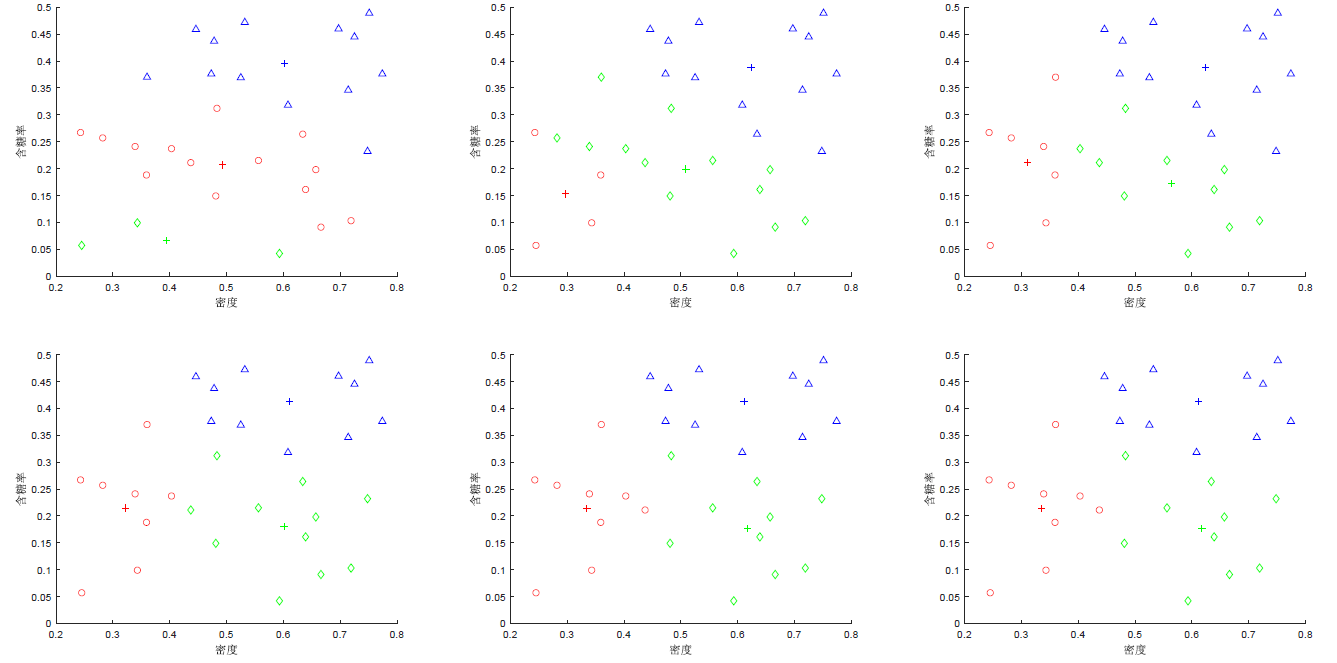
2.3.4 迭代(Iteration)

更新第一轮的均值向量后，不断重复上述过程，第六轮迭代产生的结果与第五轮迭代结果相同，于是算法停止，得到最终的簇划分。

3 K-means算法再探究

刚刚，我们对于K-means算法的基本流程有了一定的了解了。下面我们就对于刚刚算法流程遗留的一些问题予以说明。在开始之前，我们先约定一些符号。

几个参数的进一步说明

$c_i$ 最靠近$\boldsymbol{x}_i$的聚类中心的索引编号$(j=1,2,\cdots,K)$ Index of cluster $(1,2,\cdots,K)$ to which example $\boldsymbol{x}_i$ is currently assigned

$\boldsymbol{\mu}_j$ 第$j$个簇的中心（均值向量） Cluster centroid $j(\boldsymbol{\mu}_j\in\mathbb{R}^n)$

$\boldsymbol{\mu}_{c_i}$ $\boldsymbol{x}_i$所处的簇的中心（均值向量） Cluster centroid of cluster to which example $\boldsymbol{x}_i$ has been assigned

注意：其中，$c_i$是一个索引编号，也就是说是一个标量值；而$\boldsymbol{\mu}_j$和$\boldsymbol{\mu}_{c_i}$都是一个包含属性的多维向量。对于上面的西瓜数据集来说，$c_i$可以取为$1,2,3$，而$\boldsymbol{\mu}_j$和$\boldsymbol{\mu}_{c_i}$联同前面提到的$\boldsymbol{x}_i$是包含"密度"和"含糖率"两属性值的二维向量。

3.1 优化目标

第三部分的题目叫做"K-means算法再探究"。首先我们要探究的是一个名为"优化目标"的东西。在刚刚算法流程的讲述中，我们谈到了"簇分配"和"移动聚类中心"两步操作，但为什么我们可以这样来移动使得达到"聚类"的效果，这就是"优化目标"解决的问题。

3.1.1 损失代价函数

K-means算法的流程

1. Initialization: 初始化聚类中心（均值向量）；

2. Cluster assignment: 簇分配；

3. Move centroid: 移动聚类中心（均值向量）；

4. Iteration: 迭代至（局部）最优解；

这里我们先引入一个"损失代价函数"的概念。这将帮助我们更好地理解为什么我们可以通过这样简单的两步来实现"簇内相似度"最高的效果；同时也将帮助我们更好选择簇来避免局部最优的情况。

我们将需要优化的参数值也就是每个样本点所属的簇$c_i$和聚类中心的位置$\boldsymbol{\mu}_j$。我们把损失代价函数表述为这个式子，很明显右边的求和项求的就是每个样本到它对应的聚类中心的欧氏距离，这个函数实际上就是对这些距离求数学期望。

于是，我们可以很容易的得出损失代价函数和优化目标。

损失代价函数(Distortion cost function)

$J(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)=\frac{1}{m}\sum_{i=1}^m||\boldsymbol{x}_i-\boldsymbol{\mu}_{c_i}||^2$

3.1.2 优化目标

而K-means算法要做的是什么呢？就是将这个损失代价函数达到最小，这恰恰也就是我们我们所需要的"簇内相似度"最高的这个效果。但是这个式子可以直接实现吗？并不能，这是一个NP难问题，我们只能使用贪心算法来解决这个问题。

优化目标(Optimization objective)

3.2 随机初始化

说完了"簇分配"和"移动聚类中心"的理论，我们还有两个操作没有谈到，就是"初始化"和"迭代"。

3.2.1 聚类中心如何初始化？

K-means算法的流程

1. Initialization: 初始化聚类中心（均值向量）；

2. Cluster assignment: 簇分配；

3. Move centroid: 移动聚类中心（均值向量）；

4. Iteration: 迭代至（局部）最优解；

在K-means算法中，我们还有一个悬而未决的问题，到现在也没有说明。那就是如何初始化$K$个聚类中心？ 一般地，随机选择$K$个样本作为初始化的点($K<m$)，但是这样确实也会出现一些问题…

3.2.2 局部最优解(Local optima)

我们从下面三个图形可以看到，当我们取定不同的初始聚类中心后，他们的聚类结果并不相同，这是为什么呢？这是因为他们陷入了局部最优解。

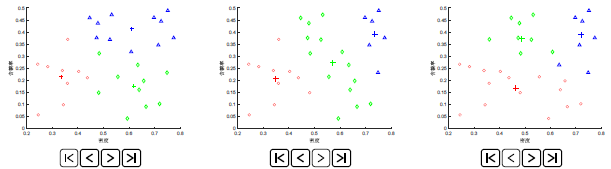
当我们随机初始化聚类中心时，很有可能聚类中心会分布在我们意想不到的地方，非常容易造成局部最优解(Local optima)。 解决这个问题的方法就是尝试多次初始化，并分别迭代到局部最优再对其损失代价函数$J(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)$分别进行比较。

3.2.3 基于随机初始化对K-means算法进行改进

下面我们对算法进行改进。刚刚我们已经说了，"初始化"的方式我们采取随机选择$K$个样本作为初始化的点来取定。为了尽可能地解决局部最优解的问题，我们采取的是"多次初始化"的方式。我们多次随机初始化迭代到最终结果，接着利用我们刚刚谈到的损失代价函数来描述各种初始化最终的效果。最后我们比较各个损失代价函数，取最小的作为我们最后的聚类结论。

基于随机初始化对K-means算法进行改进

对于西瓜数据集4.0的随机初始化

利用随机初始化100次，得到代价函数的最小值为 0.409663。

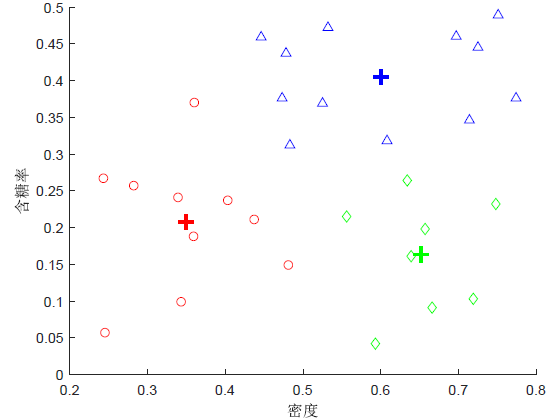
经验公式 有经验公式表明，当簇的个数$K$取为2-10时，迭代100次一般能收敛到一个比较好的结果。

3.3 簇数$K$的选择

在前面两节中，我们讨论了算法流程中四个操作的原理，但是对于输入参数我们并没有进行讨论。下面简要的介绍一下输入参数中簇数$K$的取值方式。

3.3.1 肘部法则(Elbow Method)

我们分别测试不同簇个数$K$情况下代价函数的大小，即可画出如下图的最小代价函数的折线图。仔细分辨两幅图的区别，可以发现左图在$K=3$处有一个明显转折，而右图则比较平滑。那么我们如何选择簇数$K$呢？如果出现了如左边情况的图像，则选择转折点，可以发现，当大于转折点后这个代价函数曲线的变化就不那么明显了，也就说明它趋于稳定；而往往出现的是右边的图像，比如西瓜数据集4.0。而对于右边的数据我们如何处理呢？

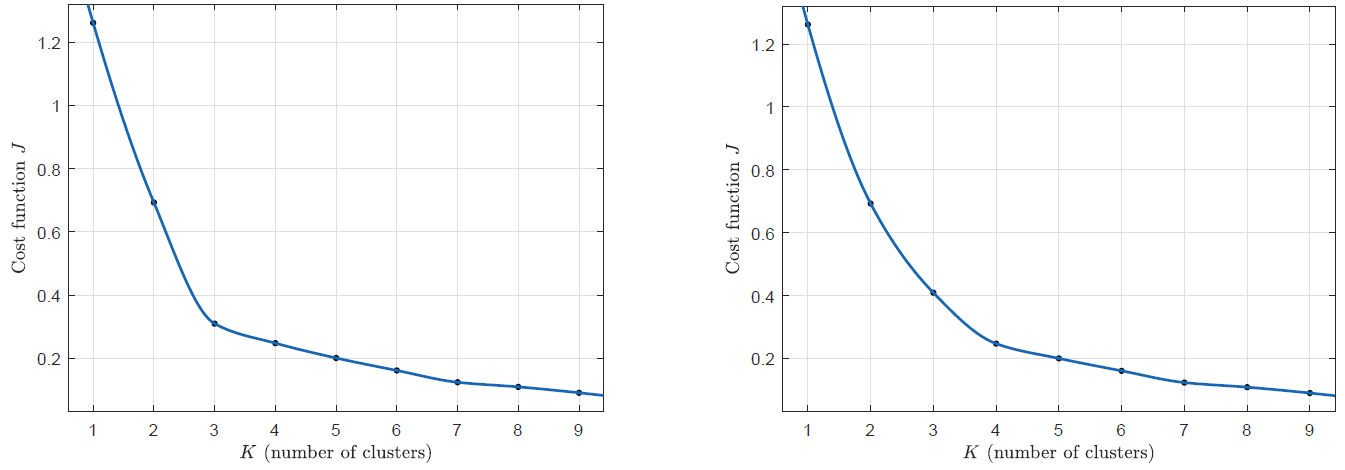
3.3.2 平滑下降时的处理方法

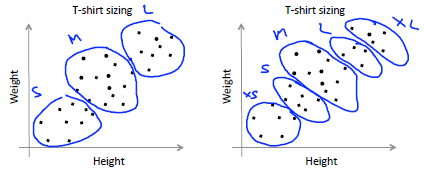
一般地，在应用K-means算法时，都是为了将得到的"簇"应用于后续的处理。所以，我们也可以根据后续处理需要的类的个数来确定K-means中簇的个数。比如我们上面的右图是西瓜数据集的"代价函数-K"曲线，而聚类可能有一个需要的结论，例如"浅色瓜"、"深色瓜"就需要两个簇；再举个吴恩达机器学习MOOC栗子：例如衬衫厂商想要根据人群的身高体重来制造不同尺寸的衬衫，如果他的心里规划是设置S、M、L三种尺寸，就分三个簇；而想要设置XS、S、M、L、XL号们就需要分五个簇。

4 K-means算法的代码实现

最后，简要的介绍一下Matlab和Python库函数对于K-means算法的支持。其中，特别需要注意的是迭代次数和随机初始化次数的区分要明确。

4.1 Matlab库函数

idx = kmeans(X,k) 执行 k 均值聚类，以将 $n\times p$ 数据矩阵 $\boldsymbol{X}$ 的观测值划分为 $k$ 个聚类，并返回包含每个观测值的簇索引的 $n\times 1$ 向量 (idx)。$\boldsymbol{X}$ 的行对应于点，列对应于变量。

[idx,C] = kmeans(___) 在 $k\times p$ 矩阵 $\boldsymbol{C}$ 中返回 $k$ 个簇质心的位置。

其中，$\boldsymbol{X}$为数据，$\boldsymbol{X}$的行对应于观测值，而列对应于变量。$k$为簇的数量。$\boldsymbol{C}$为簇质心位置，第$j$行是簇$j$的质心。

可能用到的参数

• ‘Display’ - 要显示的输出的级别：‘off’ （默认） | ‘final’（最终） | ‘iter’（迭代）

• ‘Distance’ - 距离度量： ‘sqeuclidean’ （欧氏距离） | ‘cityblock’（曼哈顿距离） 等

• ‘MaxIter’ - 最大迭代次数，默认为100

• ‘Replicates’ - 使用新初始簇质心位置重复聚类的次数，默认为1

Matlab库函数实现西瓜数据集4.0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

clear ,clc ;
data = load (’dataset .txt ’);
opts = statset (’Display ’,’iter ’);
[idx ,C] = kmeans ( data (: ,2:3) ,3,’Replicates ’ ,100, ’Options ’,opts );
hold on;
set (gcf , ’color ’,’w’);
xlabel (’密度’);
ylabel (’含糖率’);
plot (C(1 ,1) ,C(1 ,2) ,’g+’,’MarkerSize ’ ,10,’LineWidth ’ ,2);
plot (C(2 ,1) ,C(2 ,2) ,’r+’,’MarkerSize ’ ,10,’LineWidth ’ ,2);
plot (C(3 ,1) ,C(3 ,2) ,’b+’,’MarkerSize ’ ,10,’LineWidth ’ ,2);
plot ( data ( idx ==1 ,2) ,data ( idx ==1 ,3) ,’gd ’);
plot ( data ( idx ==2 ,2) ,data ( idx ==2 ,3) ,’ro ’);
plot ( data ( idx ==3 ,2) ,data ( idx ==3 ,3) ,’b^’);
hold off ;

4.2 Python库函数

首先，K-means在sklearn.cluster中，

1

from sklearn.cluster import KMeans

K-means在Python的三方库中的定义是这样的：

1

class sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm='auto')

其中，n_clusters表示的是要生成的簇的数量，n_init表示随机初始化的次数，max_iter表示最大迭代次数。

estimator =KMeans(___) 构造聚类器。其中，n_clusters表示的是要生成的簇的数量，n_init表示随机初始化的次数，max_iter表示最大迭代次数。

estimator.fit(data) 计算K-means聚类。

可能用到的参数

• label_pred = estimator.labels_ ：获取聚类标签

• centroids = estimator.cluster_centers_ ：获取聚类中心

• inertia = estimator.inertia_ ： 获取聚类准则的总和

5 总结

K-means算法的思路

for $k=1$ to 100{

随机初始化$K$个聚类中心（均值向量）$\boldsymbol{\mu}_1,\boldsymbol{\mu}_2,\cdots,\boldsymbol{\mu}_K\in\mathbb{R}^n$;

Repeat{

for $i=1$ to $m$

$c_i\leftarrow$ 最靠近$\boldsymbol{x}_i$的聚类中心的索引编号

for $j=1$ to $K$

$\boldsymbol{\mu}_j\leftarrow$ 第$j$簇所有向量的平均（均值向量）

}

得到第$k$组$c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K$;

计算代价损失函数$J_k(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)$;

}

选择使得代价损失函数$J_k(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)$最小的聚类方式。

损失代价函数(Cost function)和优化目标(Optimization objective)

$J(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)=\frac{1}{m}\sum_{i=1}^m||\boldsymbol{x}_i-\boldsymbol{\mu}_{c_i}||^2$

随机初始化(Randomly Initialization)

• 初始化方式：随机选择$K$个样本作为初始化的点$(K < m)$；

• 局部最优解：尝试多次初始化，并分别迭代到局部最优再对其损失代价函数 $J(c_1,\cdots,c_m,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K)$分别进行比较；

簇数$K$的选择(Choosing the number of clusters)

• 肘部法则 (Elbow Method)；
• 考虑后续处理需要；

参考文献

1. 周志华.机器学习[M]北京：清华大学出版社,2016:197-204.
2. 吴恩达.机器学习学习系列课程[V/OL] https://study.163.com/course/introduction.htm?courseId=1004570029&_trace_c_p_k2_=60b3accf313c45bcbd5dddc890ff4346.
3. 李航. 统计学习方法（第2版）[M] 北京：清华大学出版社, 2019.
4. MathWorks.kmeans[EB/OL] https://ww2.mathworks.cn/help/stats/kmeans.html#d122e16427.
5. Levitate_.LaTeX札记（一）：插入动画[EB/OL] https://levitate-qian.github.io/2020/06/13/latex-note-01/.
6. Levitate_.MATLAB札记（一）：让图像动起来[EB/OL] https://levitate-qian.github.io/2020/06/27/matlab-note-01/.
7. Wong, J. A. Hartiganm. A. . “Algorithm AS 136: A K-Means Clustering Algorithm.” Journal of the Royal Statistical Society. Series C (Applied Statistics) 28.1(1979):100-108.