乘法器电路总结
1 乘法器基础
1.1 开关函数
单向开关函数(阶跃函数ε(t)⟷πδ(ω)+jω1)
K1(ωct)=={1,0,uc>0,uc<0.21+π2cosωct−3π2cos3ωct+…
双向开关函数(符号函数sgn(t)⟷jω2)
K2(ωct)=={1,−1,uc>0,uc<0.π4cosωct−3π4cos3ωct+…
1.2 频域分析与滤波
-
窄带滤波器:LC并联谐振回路ω0=ωc,BWBPF=2Ω
uAM=ReIc1m[1+0.707Ic1mg1uΩmcos(Ωt−4π)]cosωct
-
宽带滤波器:LC并联谐振回路ω0=ωc,BWBPF≫2Ω
uAM=ReIc1m[1+Ic1mg1uΩmcos(Ωt)]cosωct
1.3 大小信号的区分
1.3.1 调幅
Ucm≫UΩm
- 调制信号 uΩ=UΩmcosΩt
- 载波 uc=Ucmcosωct
1.3.2 检波/解调
Ulm≫Usm
- 中频已调波 us=UsmcosΩtcosωct
- 本振信号 ul=Ulmcosωct
1.3.3 混频
Ulm≫Usm
- 中频已调波 us=Usmcosωct
- 本振信号 ul=Ulmcosωlt
1.4 利用开关函数来解决各种形式的线性时变调幅的步骤
-
判断当uc≷0时,ic(uo)的表达式。
-
利用单向/双向开关函数将ic(uo)的分段函数化为一个整体表达式。
-
若ic(uo)的表达式中出现cosωct和cosΩt的乘积项,则说明可以实现振幅调制。
-
代入开关函数,利用和差化积、积化和差等找到表达式中的普通调幅信号或双边带调幅信号。
-
合理选择中心频率和带宽,使其完成调幅,获得已调波的表达式。
2 晶体管
2.1 概念
- 非线性电路调幅中的晶体管放大器可以直接应用于线性时变电路调幅 ,除了控制调制信号是小信号而载波是大信号以外,如果晶体管是线性器件,即其转移特性在放大区线性较好,则需要使晶体管轮流工作在放大区和截止区才能对信号做非线性变换。
- 为了提高交流输出的功率和效率,电路一般将直流静态工作点设置在放大区和截止区之间的临界位置。
- 线性时变电路调幅可以利用这些特点近似分析输出电流,既而对输出电流滤波产生输出电压,得到调幅信号。
2.2 具体电路
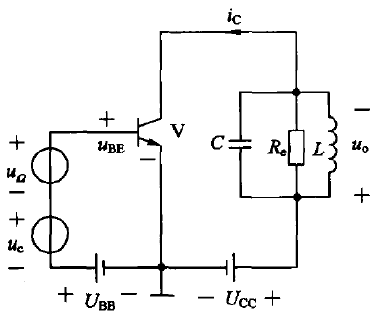
2.2.1 uΩ 和 uc都接在基极,共射组态
ic=gm(uΩ+uc)k1(ωct)
![PNP_B]()
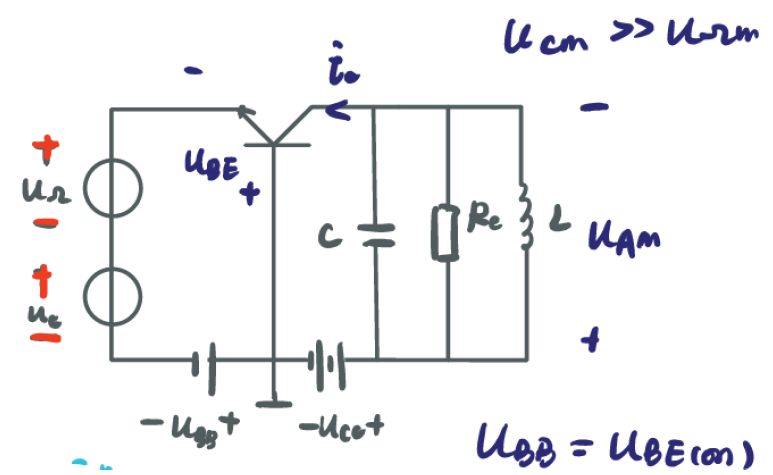
2.2.2 uΩ 和 uc 都接在射极 ,共基组态
ic=gm(uc+uΩ)(k1(ωct)−1)
![PNP_E]()
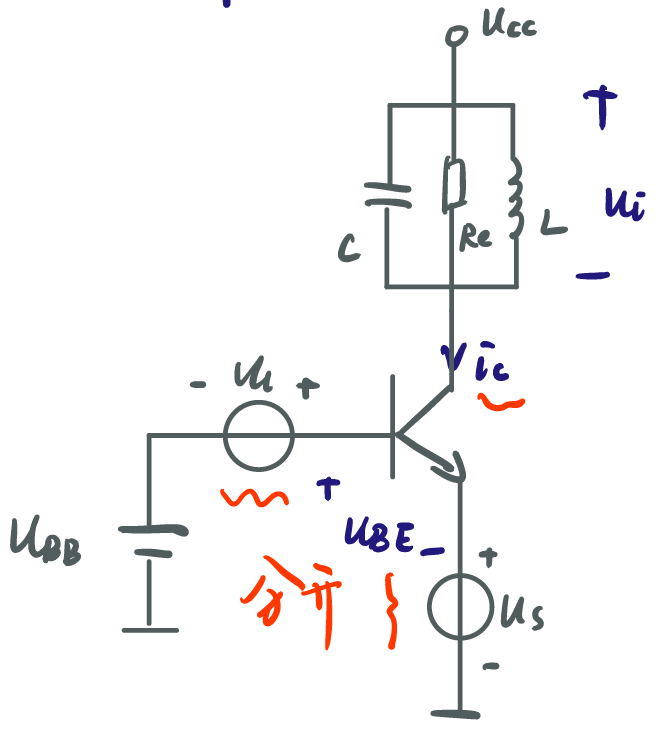
2.2.3 ul在基极,us在射极(防止频率牵引导致不稳定)
ic=gm(ul−us)k1(wlt)
![PNP_seperate]()
3 场效应管
3.1 概念
-
场效应管放大器的线性时变电路调幅与晶体管放大器的线性时变电路调幅有类似的电路结构。
-
场效应管是非线性器件,其转移特性在恒流区即为非线性,只要调制信号是小信号而载波是大信号,即使一直工作在恒流区, 放大器也可以实现线性时变电路调幅。
-
电路可以将直流静态工作点设置在场效应管的恒流区和截止区之间的临界位置,这时可以利用单向开关函数分析输出电流。
3.2 具体电路(暂略)
4 差分对放大器
4.1 概念
- 当差动放大器实现线性时变电路调幅时,调制信号和载波可以分别作为电流源的控制电压和差模输入电压,不必叠加输入。在这种分置电压的设计中,调制信号是小信号而载波是大信号不是必要条件。
- 同时,差动放大器中的两个晶体管是非线性器件,它们始终导通,不在导通和截止之间转换工作状态。
- 开关函数的引入:
- 当差模输入电压um<UT时,tanh2UTu≈2UTu;
- 当差模输入电压um>4UT时,tanh2UTu≈k2(wct);
- 之间展开为傅里叶级数。
4.2 具体电路
4.2.1、4.2.2、4.2.4中,uc和uΩ分别作为共模或差模输入时没有大小信号之分;但对于图4.2.3,这里uc和uΩ作为差模的两个端输入,则需要区分大小信号。
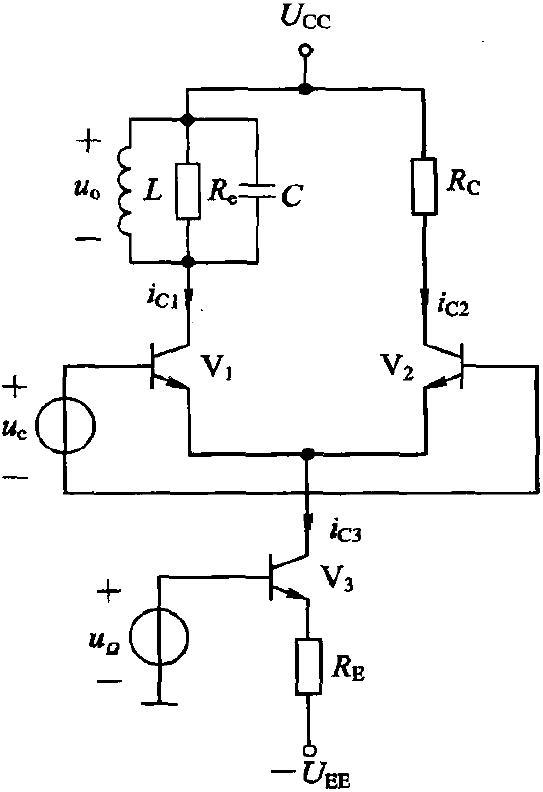
4.2.1 uc 为差模、uΩ 控制共模,且单端输出
![chafendui_1]()
ic1=2REUEE−UBE(on)(1+tanh2UTuc)+2RE1(1+tanh2UTuc)uΩ
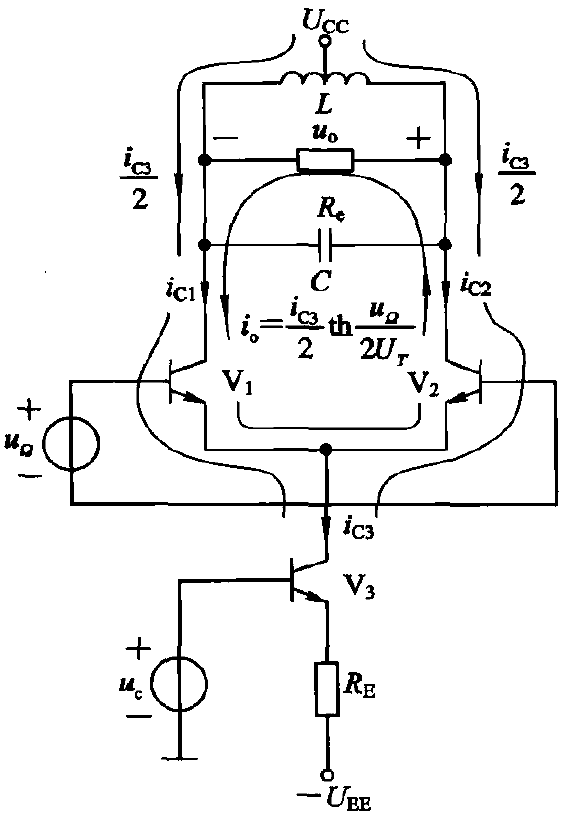
4.2.2 uΩ 为差模、uc 控制共模,且双端输出
![chafendui_2]()
io=2ic3tanh2UTuΩ
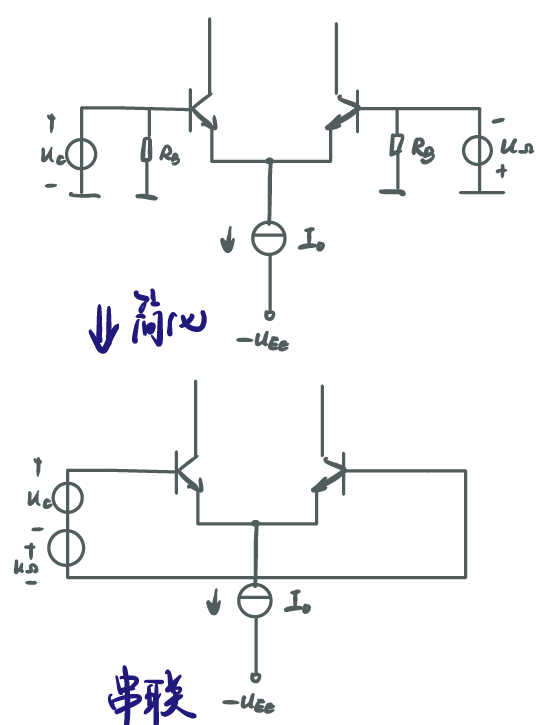
4.2.3 uΩ,uc串联
![chafendui_3]()
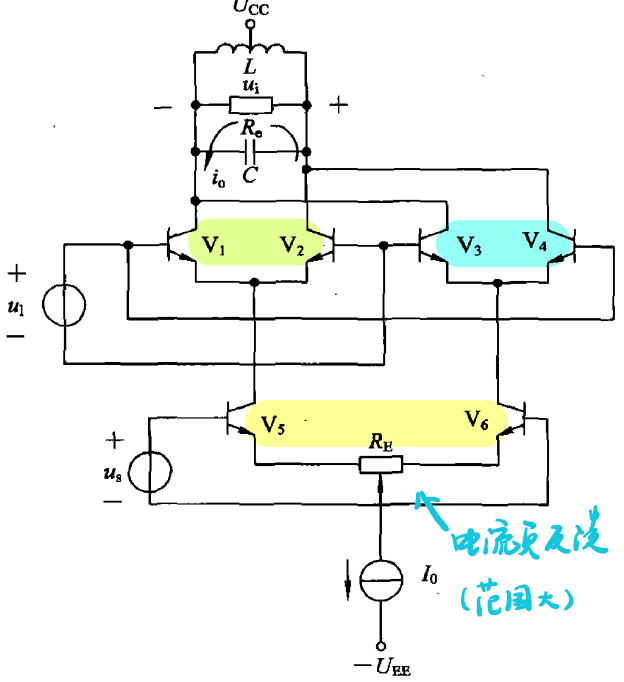
4.2.4 吉尔伯特乘法单元
![chafendui_4]()
io=2Iotanh2UTustanh2UTul
-
当小信号Usm<UT,
io=2Io2UTustanh2UTul
-
进一步当Ulm>4UT
io=2Io2UTusk2(ωlt)
5 二极管
5.1 概念
5.2 具体电路
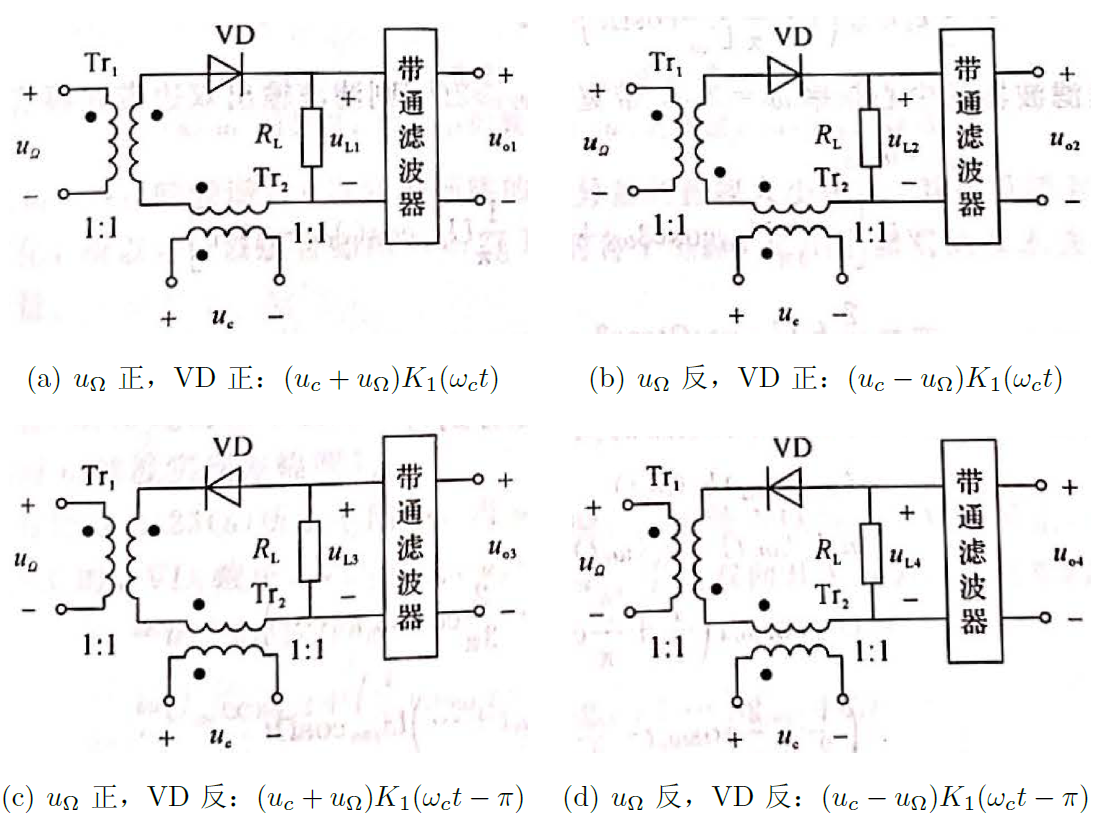
5.2.1 单二极管(4种)
![VD_singal]()
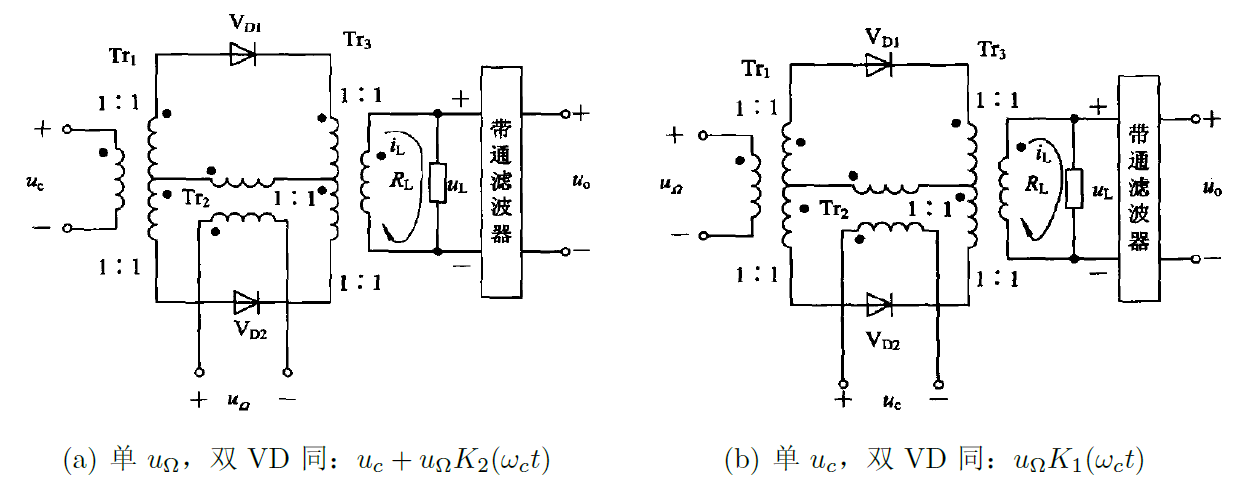
5.2.2 双二极管(2+2+1)
-
双二极管同向
![VD_double1]()
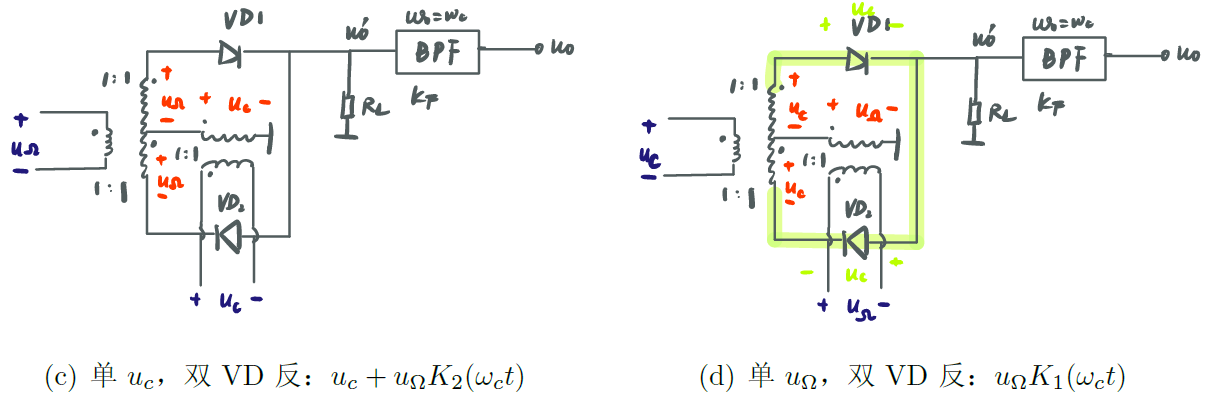
-
双二极管反向
![VD_double2]()
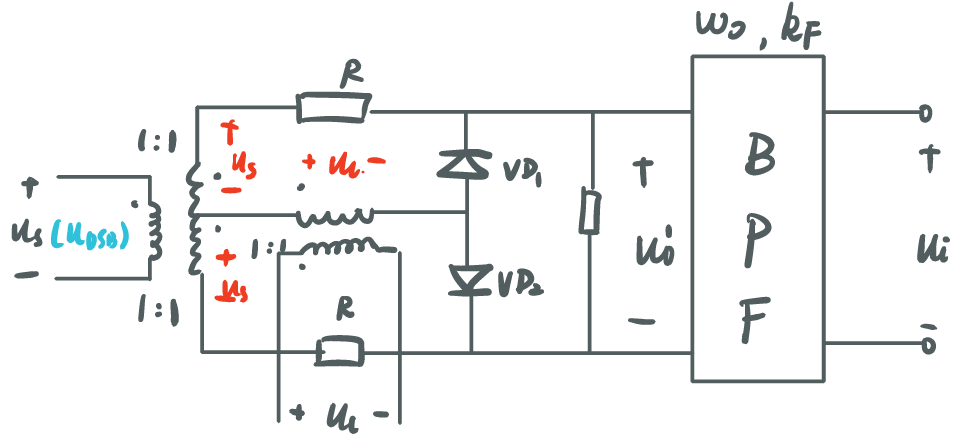
-
双二极管面对面
![VD_double3]()
uo′=2usk1(ωlt)
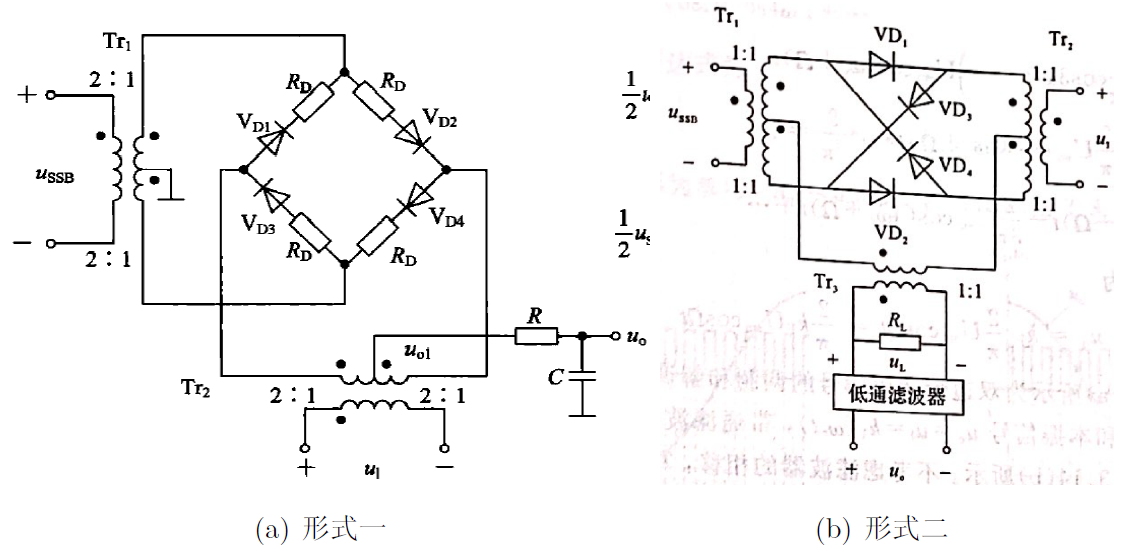
5.2.3 二极管环形乘法器(2种形式)
![VD_4]()
任选两输入、一输出
![VD_double1]()
![VD_double2]()
![VD_double3]()