MATLAB札记(一)——让图像动起来
既然在札记第一篇中谈到了在文档中插入动图,我们就势必要先获取一组动图,当然格式可以有许多种,可以是有软件生成的GIF,也可以是录屏,或者是生成的视频。这篇文章主要讲的是如何在MATLAB中使用自带的库函数获取GIF。
引入
众所周知,一般来说,我们在MATLAB中获得的图片是静态的。MATLAB能生成动态的图片是怎么回事呢?MATLAB相信大家都很熟悉,但是MATLAB能生成动态的图片是怎么回事呢,下面就让小编带大家一起了解吧。
MATLAB能生成动态的图片,其实就是MATLAB能利用一些自带的库函数生成并保存为动态GIF图片,大家可能会很惊讶MATLAB怎么会能生成动态的图片呢?但事实就是这样,小编也感到非常惊讶。
这就是关于MATLAB能生成动态的图片的事情了,大家有什么想法呢,欢迎在评论区告诉小编一起讨论哦!(没有评论区)
在使用MATLAB这个功能的过程中,找到的比较好的一篇博客是参考文献1,这篇文章写的不是特别细,但是一贴就能上手,挺好用的。也是因为讲解不是特别细,所以我做出来的图有点小问题。这里我会把我使用过程中发现的一些小问题,放在一起说。按照这篇文章的说法MATLAB绘制动态图主要用两种作用:
- 表现绘图过程,即图形的增长过程
- 表示一个参数对图形的影响
我在电磁场实验中主要用到的是第一种,即表现绘图效果(图形增长过程的)。
- Step 0:确定好绘图的函数
- Step 1:让静态的变成动态的
- Step 2:获得首帧画面
- Step 3:绘图过程——循环
- Step 4:将图像序列反向写入GIF文件中(可选)
前期准备——原理
在使用MATLAB制作动图的过程中,主要有两道工序:让图像动起来并让它延续不断、获取连续图像生成GIF文件。主要使用的函数有
- 让图像动起来并让它延续不断
getframe和moive两个函数
- 获取连续图像生成GIF文件
frame2im和imwrite
当然以上的四个函数是我在电磁场实验3中使用的。
Step 0:确定好绘图的函数
首先我们要确定好绘图函数,以及一些变量的初始化。
比如在电磁场实验1B——磁聚焦实验中,我们需要有磁聚焦的函数。
1 | cos(theta).*t,sin(theta).*(cos(t-pi)+1),sin(theta).*sin(t-pi) |
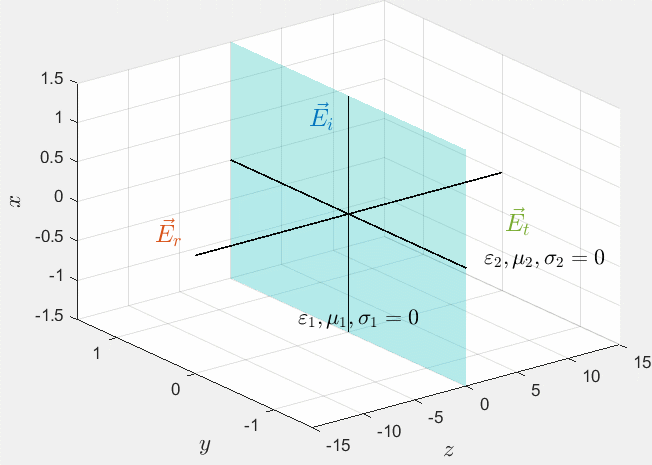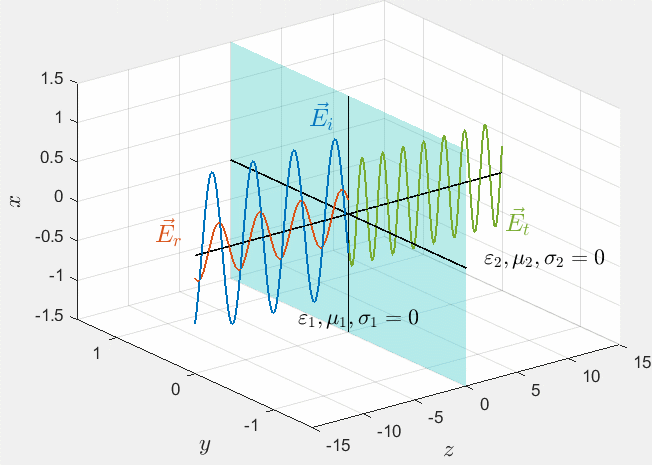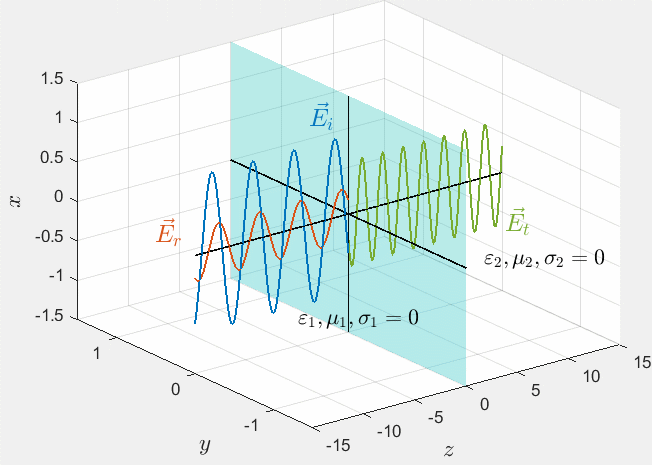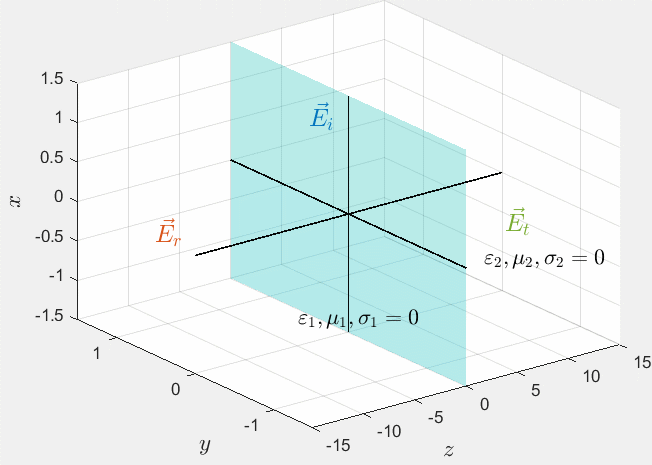
而在电磁场实验3——平面电磁波的反射和干涉实验中,我们先需要确定入射波和反射波的各项参数,并知晓入射波、反射波、合成波、透射波的方程。我们甚至可以画一个透明平面来表示介质分界面。下面是平面电磁波向理想介质垂直入射的相关前期准备。
1 | %% 初始参数设定 |
Step 1:让静态的变成动态的
首先,最关键的是我们要获得动图。获取动图我了解到的有两个办法:
法Ⅰ:不考虑生成GIF,只要求能在MATLAB中看到动效。
比如在电磁场实验1中使用的彗星图comet3函数。彗星图是动画图,其中一个圆(彗星头部)跟踪屏幕上的数据点。彗星主体是位于头部之后的尾部。尾巴是跟踪整个函数的实线。comet3(x,y,z) 显示经过点 曲线的彗星图。但这个comet3函数暂没有找到什么比较好的获取GIF办法。下图时使用comet3函数获得的一个磁聚焦实验的图像。其基本动画函数为
1 | t=0:0.01:2*pi; |
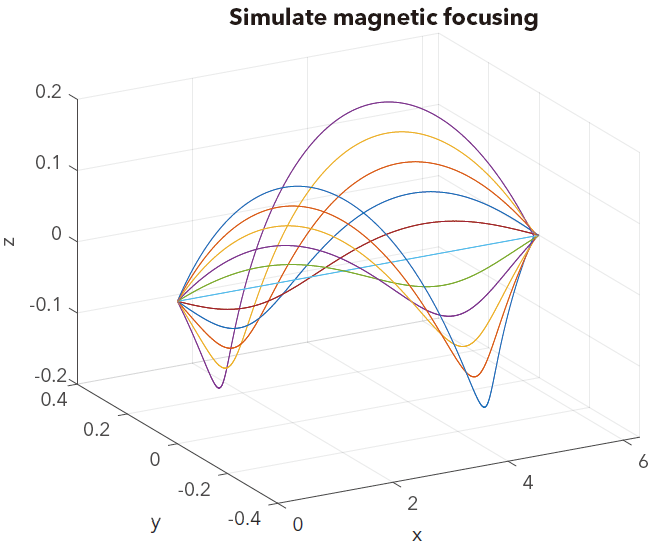
这种方法有利有弊,但弊大于利。主要问题就是他没法导出成比较有效果的GIF,导出成GIF需要获取动作每一帧的图像,而这个函数在绘制每一条线的时候的中间帧我们是无法获得的,硬性去套用获取GIF的函数,只能画出这样的图。
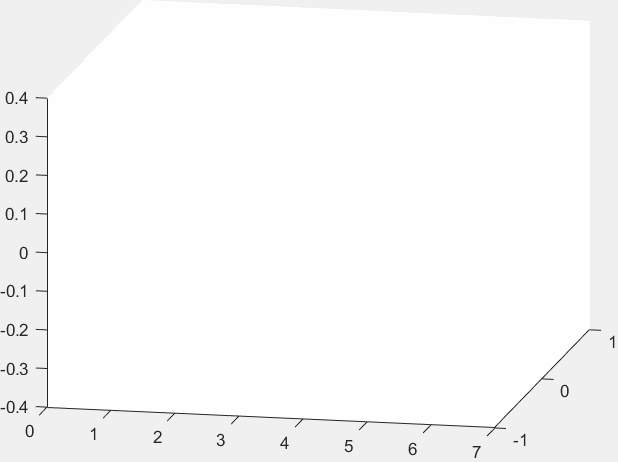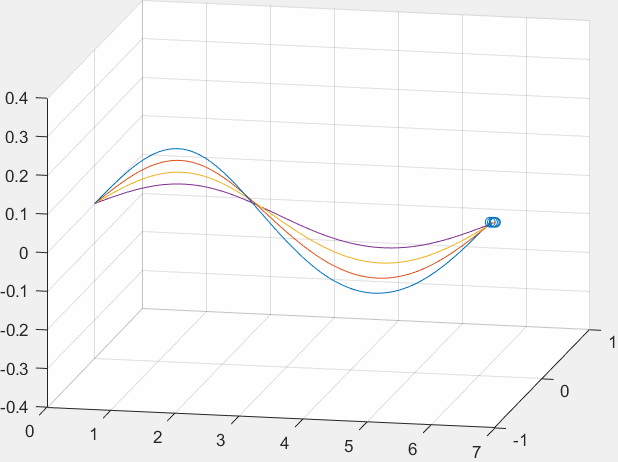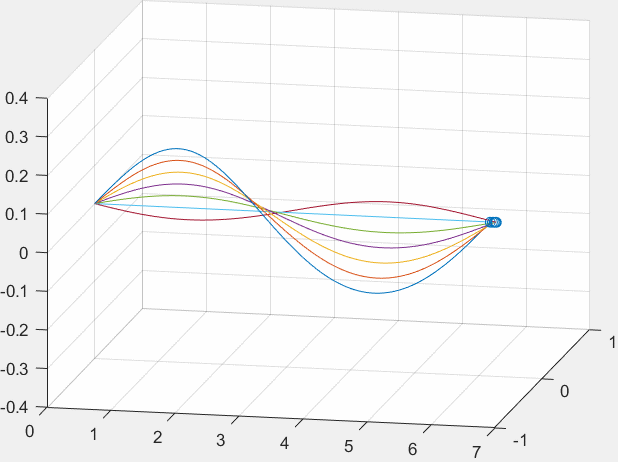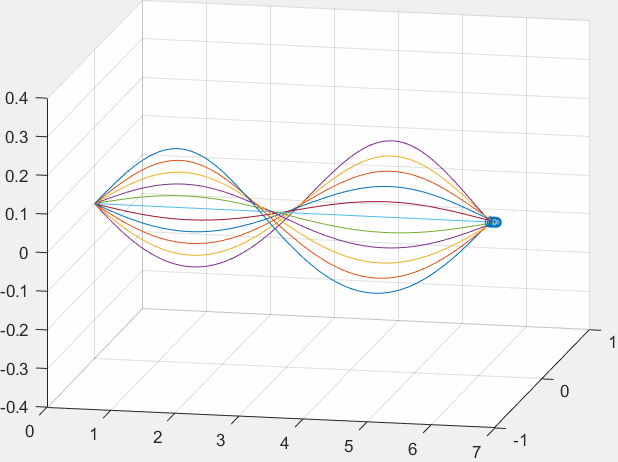
法Ⅱ:利用堆叠关系,或者有动态效果的图。
如果我们把曲线分成很多小段,让每个小段依次显示,我们是不是也能获得动态的图片呢?答案是肯定的,但是我们无法让图片一起显示之前显示过的小段和当前我们所需要出现的小段,所以这里我们不妨采用堆叠的关系,这是什么意思呢?请看下面的图片我们就能大致知道意思了(第一次画这样的图,画的效果并不好)
❗值得注意的是:这里的小段只是我形象化的表现,而到对这些小段取极限,取到无穷小时,小段就变成了一个个的点。
同理,我们的堆叠操作也是每次在前一张画面上生成一个点。
这里我们选用的就是法Ⅱ。但是很显然法Ⅱ也会有一定的问题,我们最终得到的线其实是这么多线堆叠而成的,我们要对线条进行操作就会变得异常复杂。**尤其当我们需要导出最终图像的矢量格式时,甚至会出现断点问题,这点在有两条重叠线的情况下最甚。**请看下图“平面电磁波向理想导体垂直入射的仿真结果”。
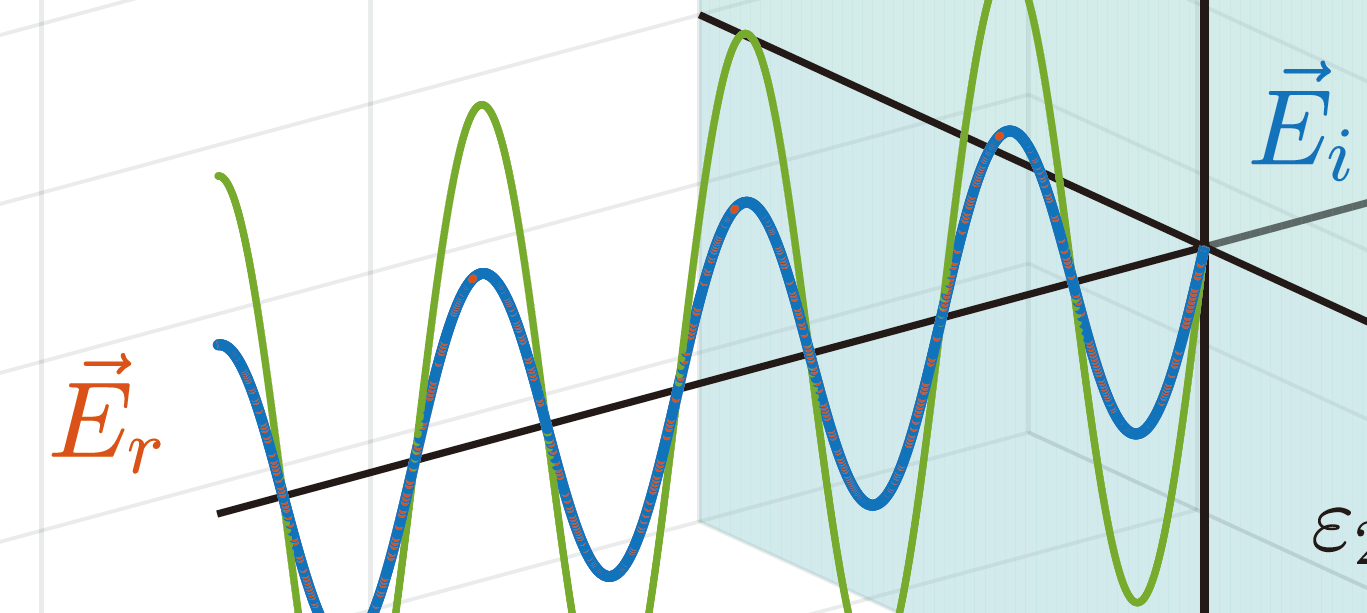
从图中我们显然能够发现,入射波和反射波的曲线重叠在了一起,而橙色的反射波点被掩盖在蓝色的入射波点下,但又有时会隐隐约约的透出来。
关键步骤——利用函数写进GIF中
Step 2:获得首帧画面
首先,根据需要,我们需要确定首幅图的样式,并指定标题,坐标轴标题等样式。(这步可以省略)
接着,为确保图像在采集的过程中包括坐标轴及标题,并在在指定的范围内获得图像文件,我们需要下列代码。(这段代码可以直接使用,不需要改动)
1 | %确保图像在采集的过程中包括坐标轴及标题 |
然后,创建gif文件,指定其样式,写入首帧图像。这里的lab032.gif就是我们生成GIF图片的名称,注意下面和这个名称要对应哦!
1 | %创建gif文件,指定其样式,写入首帧图像 |
❗值得注意的是
- 一般的,如果你把Step 2写在循环中,就会循环往复的生成第一帧,而你的GIF就只剩两帧了。但是我们可以通过条件语句
if去判定,当前处在哪一帧,if(j==1)那么我们将运行绘制首帧的代码。同理,我们可以还可以在if(j==1)中放置一些初始化的语句。- 如果我们将上述代码放置在循环外,我们则需要注意考虑图像的持续显示,即
hold on函数的使用。
Step 3:绘图过程——循环
绘图过程我们可以把它放在一个for循环中。根据Step 1中所讲的,我们采用堆叠的方式去生成动态图像,,每一帧也就对应for循环中的一步,所以我们在for循环中每一步就需要生成从最原始点到目前帧需要出现画面的整条曲线。
在循环中,我们首先绘制我们的图像,例如平面电磁波向理想介质垂直入射一些绘图函数代码的书写。(程序的核心)
1 | % 绘图前预备 |
接着,我们再次获取该帧的GIF图像。(获取GIF的核心,这段代码可以直接使用,不需要改动)
1 | %下面是制作gif的主要代码,除了调节间隔时间外,一般不需要改动 |
最后,我们对for循环进行+1操作,进入下一次循环。
Step 4:将图像序列反向写入GIF文件中(可选)
这个就是坑到我的地方了。其实我的平面电磁波向理想介质垂直入射并不需要反向写入的过程。如果反向写入后,Step 2中法Ⅱ所对应GIF所表现出的时序就是下图这样的。
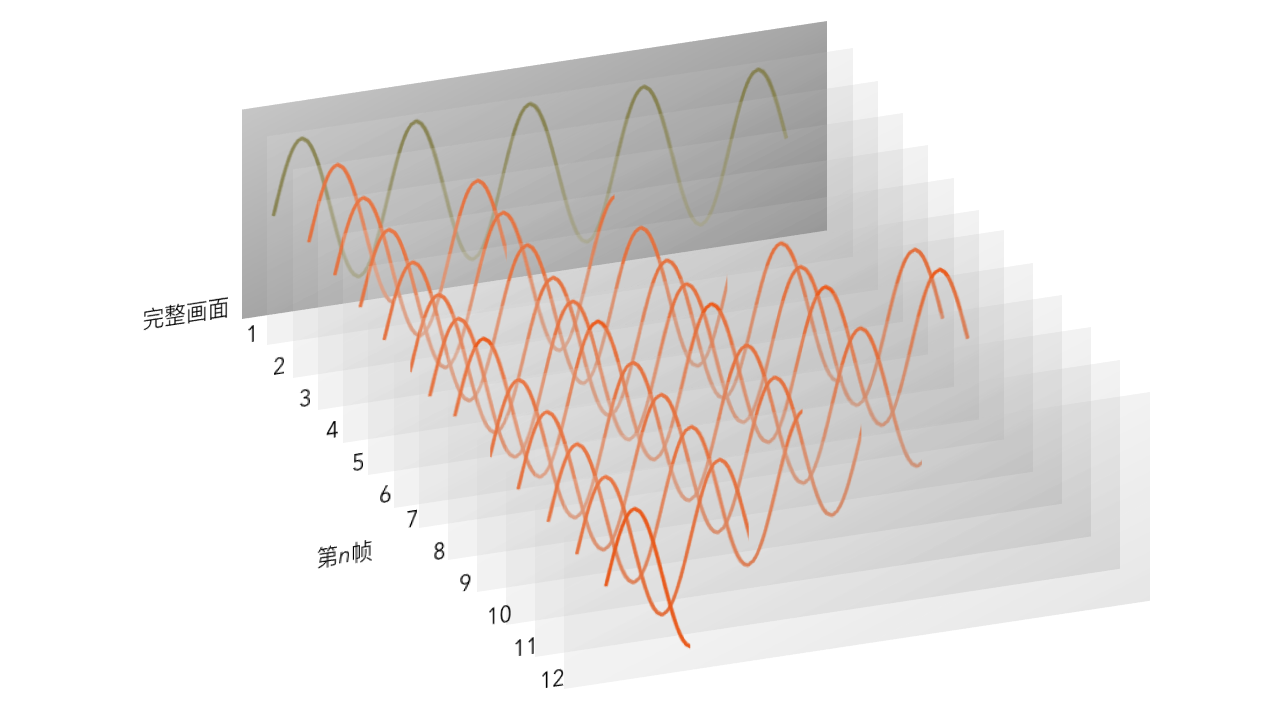
有需要的读者可以使用下列代码。
1 | %将图像按相反的顺序再写入到gif中 |
例子
〔案例1〕平面电磁波向理想介质垂直入射的仿真结果
1 | %% Normal incidence to ideal medium |
❗值得注意的是
如果我们将制作GIF的代码注释掉转而保留
2
3
4
5
%% Function to play animation
for i=1:10
movie(N,1,30);
end我们就可让这个动画效果播放10遍。利用的就是
getframe获取帧函数和moive播放函数了。
〔案例2〕
来自参考文献1
1 | %适用于在一幅图中表现给图过程,即图形的增长过程 |
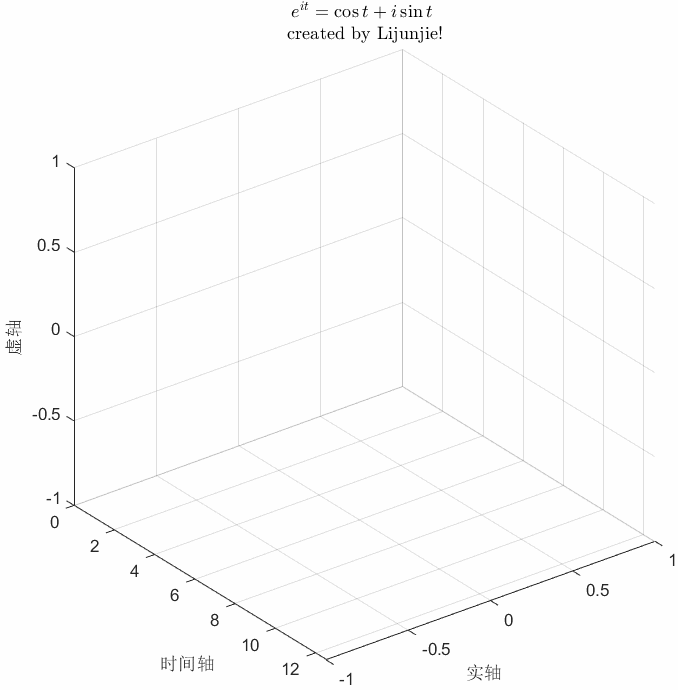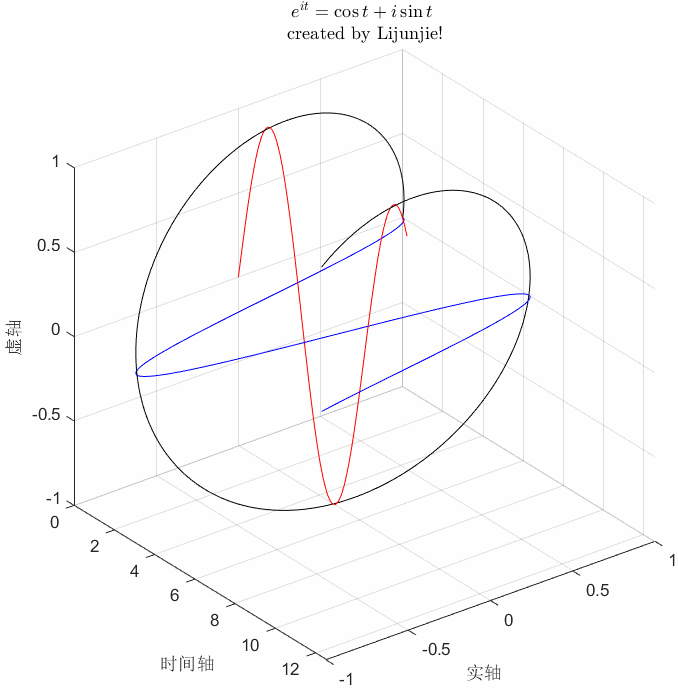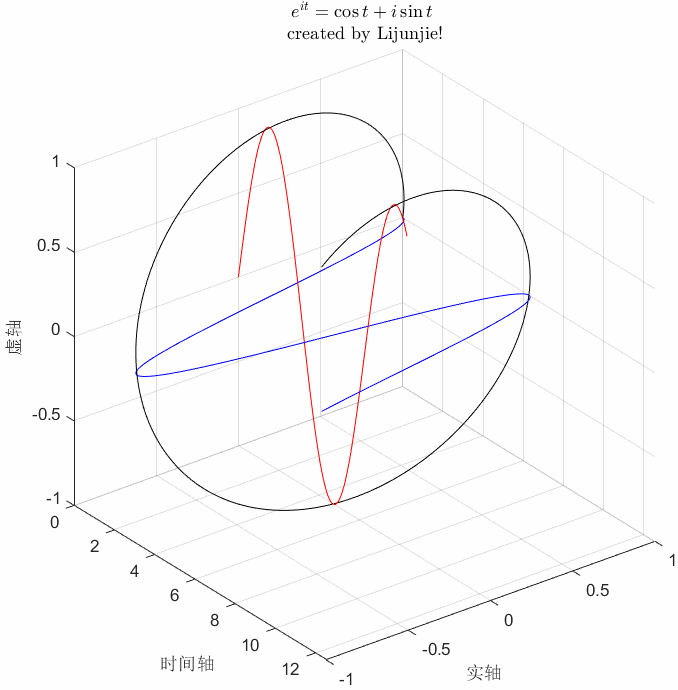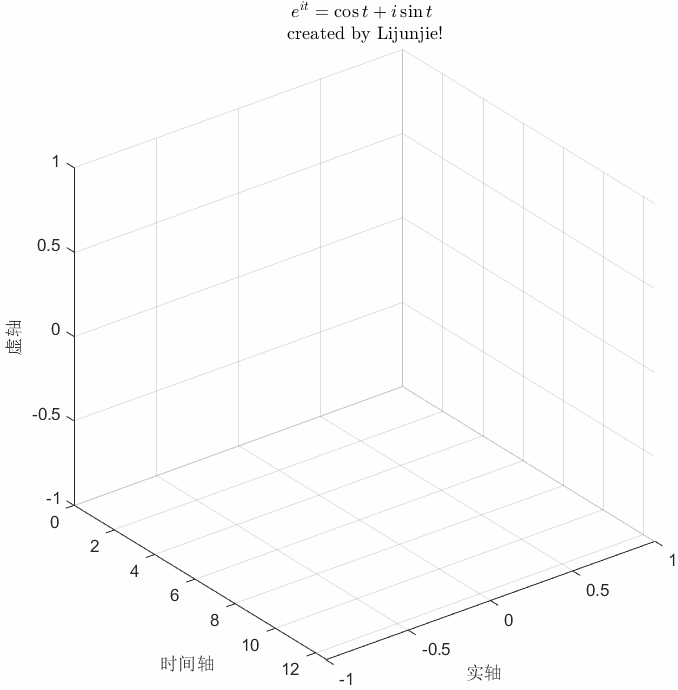
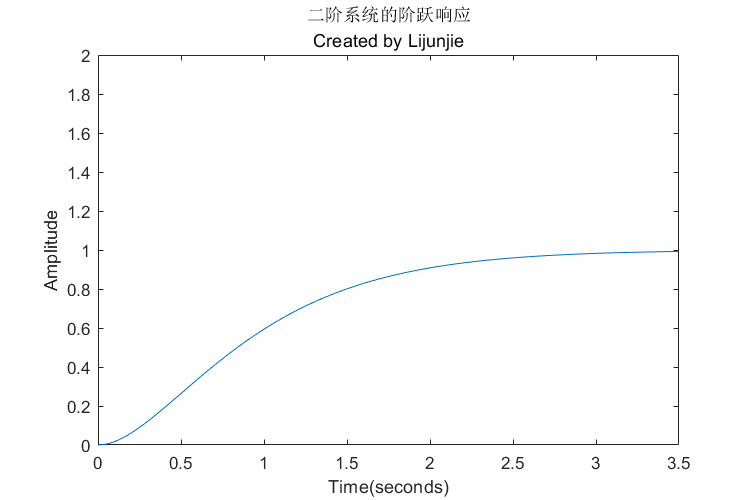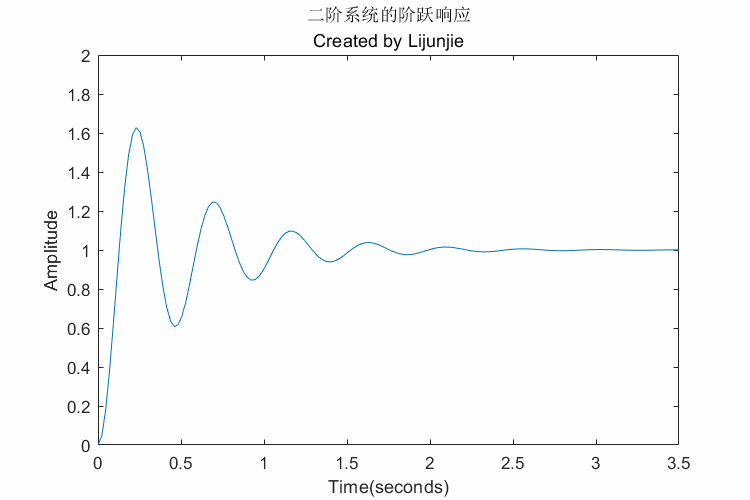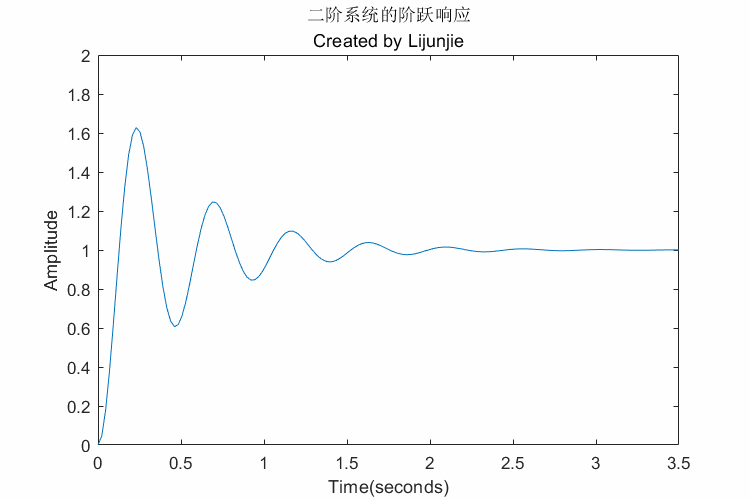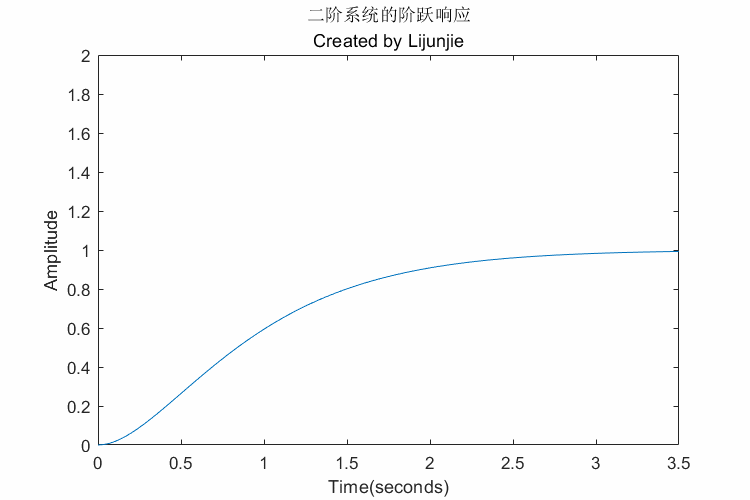
〔案例3〕二阶系统的极点、频率特性
来自参考文献1
1 | function second_order_system_gif_1() |

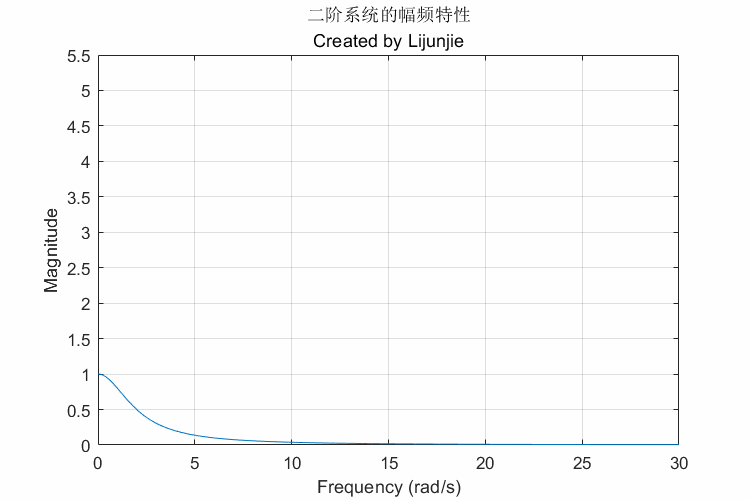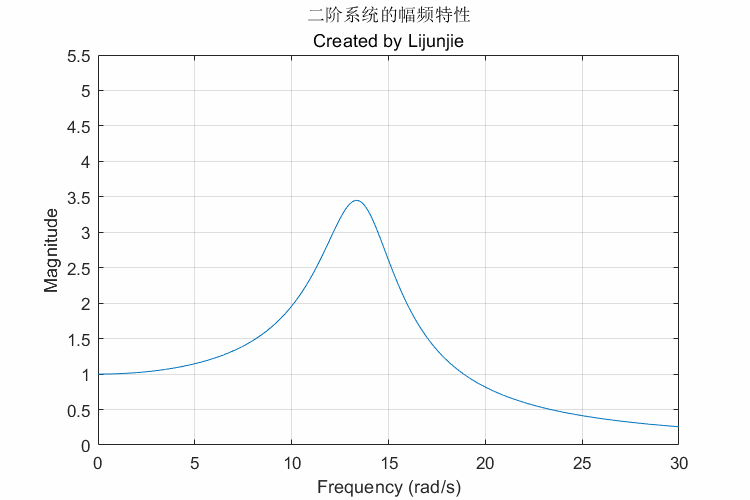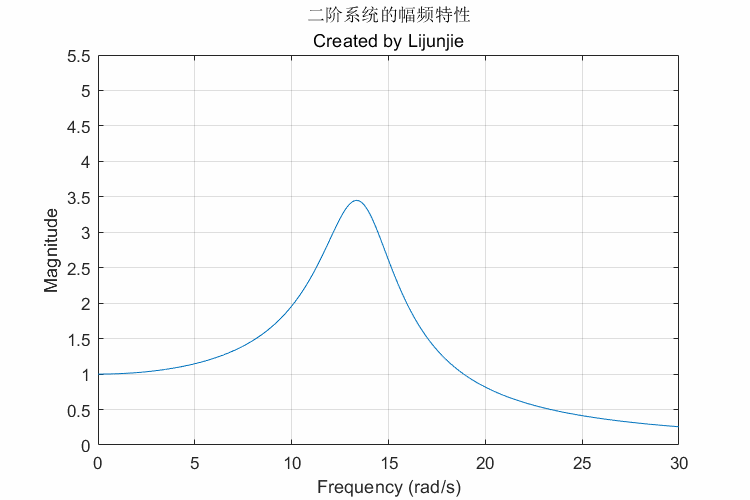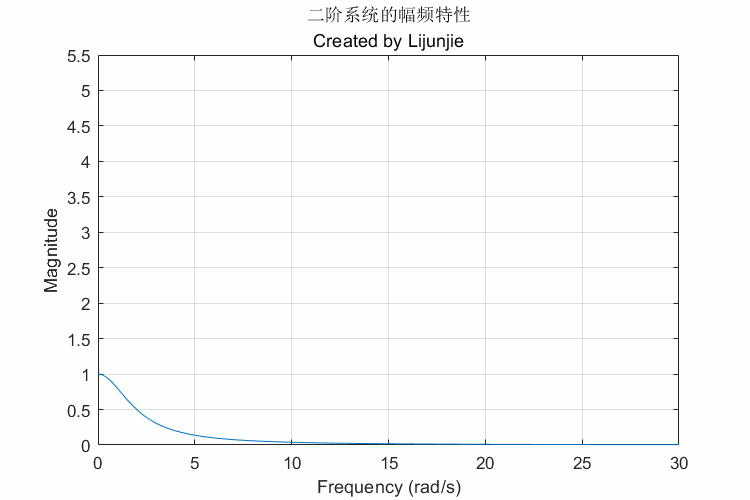
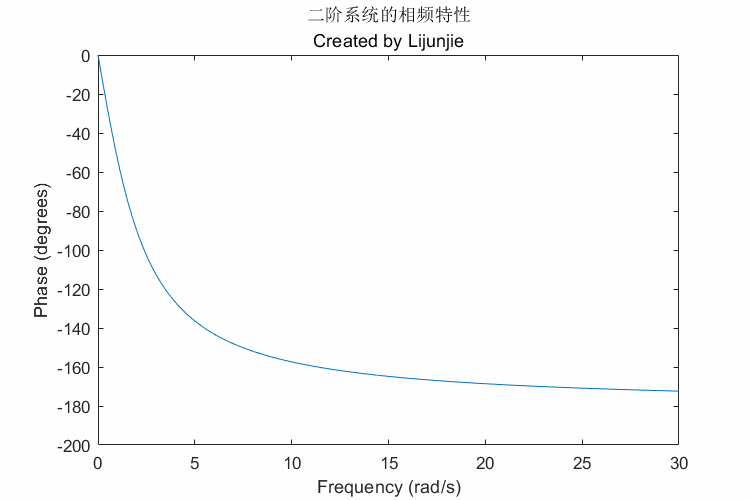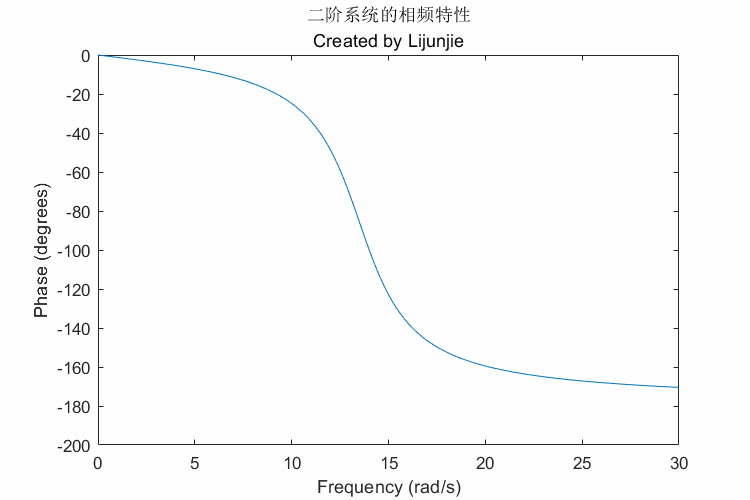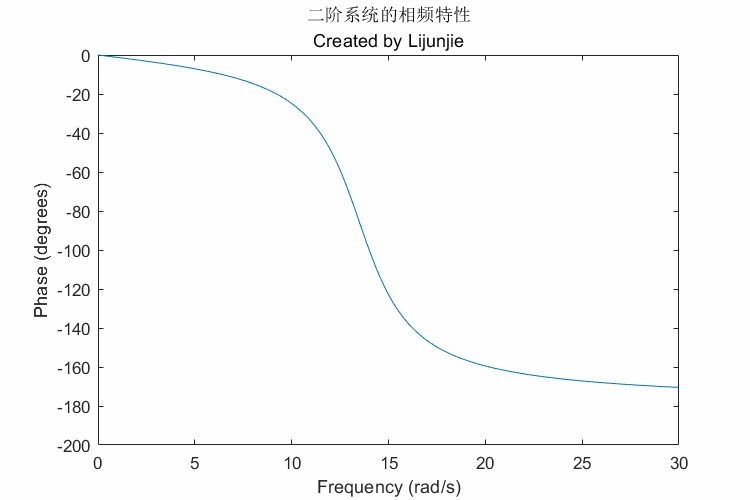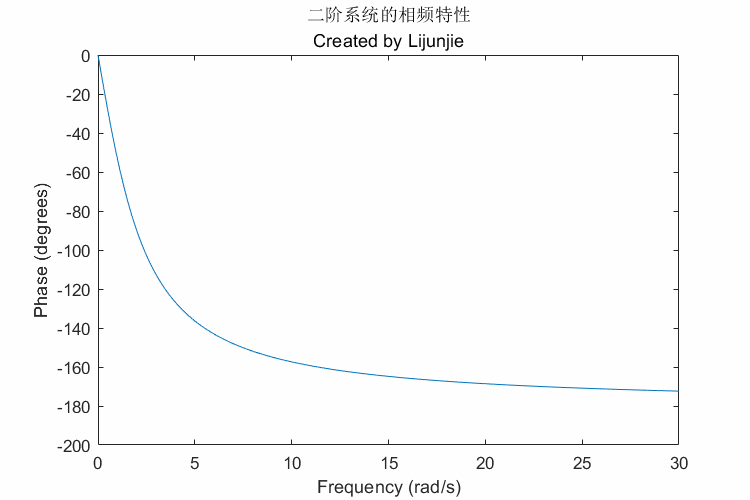
一些注意事项
- 这个功能搭配札记第一篇,即可在制作的PDF中播放动画效果了,还是很炫酷。
- 这样制作的图片清晰度还可以,但是还是图片质量存在一定的损失的,但是看上去还可以。
- 这样制作的图像最后获得矢量图,可能会存在一定的小问题:尤其当我们需要导出最终图像的矢量格式时,甚至会出现断点问题,这点在有两条重叠线的情况下最甚。
- 代码基本可以直接套用,需要更改的地方不是很多,建议看懂Step 4,再去使用反向写入功能,其实大部分情况下,我们是不需要反向写入的。
参考文献
- 木子识时务.Matlab绘制动态 .gif 图[EB/OL].https://www.jianshu.com/p/cd9501bc810a.2017-08-20/2020-06-27.
